関数列$\{f_n\}$に対して,
\begin{align*}\lim_{x\to a}\sum_{n=1}^{\infty}f_n(x)=\sum_{n=1}^{\infty}\lim_{x\to a}f_n(x)\end{align*}
と極限$\lim$と和$\sum$の順序交換をしたいことがよくあります.また,
\begin{align*}\frac{d}{dx}\sum_{n=1}^{\infty}f_n(x)=\sum_{n=1}^{\infty}\frac{df_n}{dx}(x)\end{align*}
と微分$\frac{d}{dx}$と和$\sum$の順序交換をしたいこともよくあります.
これらの順序交換が可能であることが保証できる条件はいくつか知られていますが,この記事では測度論から証明されるものを紹介します.
この記事では
- 極限$\lim$と級数$\sum$の順序交換
- 微分$\frac{d}{dx}$と級数$\sum$の順序交換
- 極限・微分と級数の順序交換条件の定理の証明
を順に解説します.
条件自体は測度論を知らなくても問題なく読めるので,とりあえず使えればよいという人は結果だけ知っておくのも良いでしょう.
極限$\lim$と級数$\sum$の順序交換
極限と級数の順序交換ができるための十分条件について説明し,具体例を考えましょう.
極限と級数の順序交換ができるための十分条件
[極限と級数の順序交換条件]$I\subset\R$を開集合とし,$a\in I$と,$I$上の実数値関数列$\{f_n\}_{n\in\N}$を考える.任意の$n\in\N$に対して,極限$\lim_{x\to a}f_n(x)$は収束するとする.このとき,ある実数列$\{M_n\}$が存在して,
- 任意の$x\in I$に対し$|f_n(x)|\le M_n$
- $\{M_n\}$は総和可能:$\sum_{n=1}^{\infty}M_n<\infty$
を満たすなら,
\begin{align*}\lim_{x\to a}\sum_{n=1}^{\infty}f_n(x)=\sum_{n=1}^{\infty}\lim_{x\to a}f_n(x)\end{align*}
が成り立つ.
この定理を使うためのポイントは
- 極限$\lim_{x\to a}f_n(x)$が収束し
- 任意の$x\in I$に対し$|f_n(x)|\le M_n$となる実数列$\{M_n\}$が存在し
- $\sum_{n=1}^{\infty}M_n<\infty$を満たす
という3つを示すことです.
この定理は測度論により証明できます.微分積分学でも微分と級数の順序交換条件を学びますが,微分積分学で証明されるものとは少々異なります.微分積分学では一様収束性を課す定理を学ぶことが普通ですが,測度論により証明できる上の定理は一様収束性を示さなくてもよい点が優れています.
具体例1($\lim\limits_{x\to1}\sum\limits_{n=1}^{\infty}\dfrac{1}{n^2+nx}$)
次の極限を求めよ.
\begin{align*}\lim_{x\to1}\sum_{n=1}^{\infty}\frac{1}{n^2+nx}\end{align*}
極限と級数の順序交換ができれば,
\begin{align*}\lim_{x\to1}\sum_{n=1}^{\infty}\frac{1}{n^2+nx}=\sum_{n=1}^{\infty}\frac{1}{n^2+n}\end{align*}
となって,部分分数分解を用いて計算できる級数になって計算できますね.
関数$f_n:(0,2)\to\R_{\ge0}$を$f_n(x)=\frac{1}{n^2+nx}$により定める.任意の$n\in\{1,2,\dots\}$に対して極限
\begin{align*}\lim_{x\to1}f_n(x)=\frac{1}{n^2+n}=\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}\end{align*}
が存在し,任意の$x\in(0,2)$に対して
\begin{align*}&|f_n(x)|\le\frac{1}{n^2},
\\&\sum_{n=1}^{\infty}|f_n(x)|=\sum_{n=1}^{\infty}\frac{1}{n^2}<\infty\end{align*}
なので,[極限と級数の順序交換条件]の定理より極限と級数の順序交換ができて
\begin{align*}&\lim_{x\to1}\sum_{n=1}^{\infty}\frac{1}{n^2+nx}
=\sum_{n=1}^{\infty}\bra{\frac{1}{n}-\frac{1}{n+1}}
\\&=\lim_{N\to\infty}\sum_{n=1}^{N}\bra{\frac{1}{n}-\frac{1}{n+1}}
=\lim_{N\to\infty}\bra{\frac{1}{1}-\frac{1}{N+1}}=1\end{align*}
を得る.
いまの解答例では$f_n$の定義域を$(0,2)$としましたが,$x\to1$のときの極限の定義と$|f_n|$の評価ができれば良いので,$f_n$の定義域は$(\frac{1}{2},\frac{3}{2})$などでも構いません.
微分$\frac{d}{dx}$と級数$\sum$の順序交換
次に,微分と級数の順序交換ができるための十分条件について説明し,具体例を考えましょう.
微分と級数の順序交換ができるための十分条件
[微分と級数の順序交換条件]$I\subset\R$を開集合とし,$I$上の実数値関数列$\{f_n\}_{n\in\N}$を考える.任意の$n\in\N$に対して,$f_n$は$I$上微分可能であるとする.任意の$x\in I$に対して,実数列$\{f_n(x)\}_n$の級数は収束するとし
\begin{align*}F(x)=\sum_{n=1}^{\infty}f_n(x)\end{align*}
とおく.このとき,ある実数列$\{M_n\}$が存在して,
- 任意の$n\in\N$と$x\in I$に対して$|{f_n}'(x)|\le M_n$
- $\{M_n\}$は総和可能:$\sum_{n=1}^{\infty}M_n<\infty$
を満たすなら,$F$は$I$上微分可能で
\begin{align*}F'(x)=\sum_{n=1}^{\infty}{f_n}'(x)\end{align*}
が成り立つ.
結論の$F$を書き直せば
\begin{align*}\frac{d}{dx}\sum_{n=1}^{\infty}f_n(x)=\sum_{n=1}^{\infty}{f_n}'(x)\end{align*}
ですから,この定理は微分と級数の順序交換が可能であるための十分条件を述べる定理になっているわけですね.
関数$F$が微分できるかどうかを議論するためにはそもそも$F$が定義されていないといけませんから,「任意の$x\in I$に対して実数列$\{f_n(x)\}_n$の級数は収束する」という条件があるわけですね.
なので,この定理を使う際のポイントは
- $|{f_n}'(x)|\le M_n$を満たす実数列$\{M_n\}$をとる
- $\sum_{n=1}^{\infty}M_n<\infty$を満たす
の2つを示すことですね.
具体例2($\dfrac{d}{dx}\sum\limits_{n=1}^{\infty}e^{-nx}$)
$I=(0,\infty)$とする.関数$F:I\to\R$が
\begin{align*}F(x)=\sum_{n=1}^{\infty}e^{-nx}\end{align*}
で定義できることを示し,$F$は微分可能で
\begin{align*}F'(x)=-\sum_{n=1}^{\infty}ne^{-nx}\end{align*}
となることを示せ.
任意の$n\in\{1,2,\dots\}$に対して,関数$f_n:I\to\R$を$f_n(x)=e^{-nx}$により定める.
関数$F:I\to\R$が定義できることの証明
任意に$x\in I$をとる.実数列$\{f_n(x)\}_n$は初項$e^{-x}$,公比$e^{-x}<1$の等比数列で,
\begin{align*}\sum_{n=1}^{\infty}|e^{-nx}|=\frac{e^{-x}}{1-e^{-x}}<\infty\end{align*}
と絶対収束する.よって,関数$F:I\to\R$が定義できる.
微分と級数の順序交換により導関数$F’$を求める
任意に$\delta>0$を固定する.$f_n$は$(\delta,\infty)$上微分可能で,任意の$n\in\{1,2,\dots\}$, $x\in(\delta,\infty)$に対して
\begin{align*}|{f_n}'(x)|=\abs{-ne^{-nx}}\le ne^{-\delta n}\end{align*}
が成り立つ.さらに,
\begin{align*}\sum_{n=1}^{\infty}ne^{-\delta n}<\infty\end{align*}
だから実数列$\{ne^{-\delta n}\}$は総和可能である.
よって,[微分と級数の順序交換条件]の定理より,$F$は$(\delta,\infty)$上微分可能で,微分と級数の順序交換ができ,$\delta$によらず
\begin{align*}F'(x)=\sum_{n=1}^{\infty}(f_n)'(x)=-\sum_{n=1}^{\infty}ne^{-nx}\quad\dots(*)\end{align*}
を得る.$\delta>0$は任意なので,$F$は$I$上微分可能で$(*)$を得る.
後半で微分可能性を示す際,最初から$I$全体で考えると上からの評価で$e$の負冪$e^{-\delta n}$を残せず上手くいかないため$(\delta,\infty)$で考えています.
この例のように指数関数を残すために,任意に$\delta>0$をとって$t$の下限を0から少し浮かせてから評価する方法はよく用いられるので知っておきたいところです.
極限・微分と級数の順序交換条件の定理の証明
ルベーグ積分論には,極限とルベーグ積分の順序交換ができるための条件を述べたルベーグの収束定理があります.ルベーグの収束定理はルベーグ測度空間でなくとも,任意の測度空間上でも同様に成り立ちます.
そこで,とくに$\N$の部分集合の元の個数を測る測度空間である計数測度空間$(\mathbb{N},2^{\mathbb{N}},\mu)$でルベーグの収束定理を用いたものが,実は上で紹介した[極限と級数の順序交換条件]の定理になります.
ここでは,計数測度空間とルベーグの収束定理を確認し,[極限と級数の順序交換条件]の定理,[微分と級数の順序交換条件]の定理を証明します.
計数測度空間は元の個数を数える測度
正の整数全部の集合$\N$と$\N$の冪集合$2^{\N}$の組$(\mathbb{N},2^{\mathbb{N}})$は可測空間です.
この可測空間$(\mathbb{N},2^{\mathbb{N}})$に対して,関数$\mu:2^{\N}\to\R\cup\{\infty\}$を
\begin{align*}\mu(\{n_1,n_2,\dots,n_r\})=r,\quad
\mu(\{n_1,n_2,\dots\})=\infty\end{align*}
で定めます.すなわち,$\mu$は$\N$の部分集合の元の個数を数える関数ということですね.
このとき,$(\mathbb{N},2^{\mathbb{N}},\mu)$は測度空間となり,この測度空間を計数測度空間(または数え上げ測度空間など)といいます.
測度空間上の積分の定義より,計数測度空間$(\mathbb{N},2^{\mathbb{N}},\mu)$において,$S\in2^{\mathbb{N}}$($S\subset\N$)上の可測関数$\{a_n\}_{n\in S}$における積分は
\begin{align*}\int_{S}a_n\,d\mu(n)=\sum_{n\in S}a_n\end{align*}
と和になりますね.
ルベーグの収束定理と使うための3つのポイント
通常のルベーグの収束定理は次のように極限とルベーグ積分の順序交換ができるための十分条件を述べた定理ですね.
[ルベーグの収束定理]$I\subset\R$を開集合,ルベーグ可測集合$A$とし,$a\in I$と,$A$上のルベーグ可測関数の族$\{f_t\}_{t\in I}$を考える.関数列$\{f_t\}_{t\in I}$が$A$上ルベーグほとんど至るところで各点収束し,($t$によらない)ある$A$上の関数$g$が存在して,
- 任意の$t\in I$に対して$|f(x,t)|\le g(x)$ a.e. $x\in A$
- $g$は$A$上ルベーグ可積分:$\int_{A}g(x)\,dx<\infty$
を満たすなら,極限$\lim_{t\to a}\int_{A}f_t(x)\,dx$が存在して
\begin{align*}\lim_{t\to a}\int_{A}f_t(x)\,dx=\int_{A}\lim_{t\to a}f_t(x)\,dx\end{align*}
が成り立つ.
ルベーグの収束定理を使う際には
- 関数列が(ほとんど至るところ)各点収束する
- 任意の$t\in I$に対して(ほとんど至るところ)$|f_t|\le g$を満たす関数$g$をとる
- $\int_{A}g(x)\,dx<\infty$を満たす
の3つを示すことが大切なのでした.
標準的なルベーグの収束定理は関数列$\{f_n\}$に対するものですが,上記のように区間$I$を添え字集合とする関数族$\{f_t\}_{t\in I}$に対しても同様に成り立ちます.
極限と級数の順序交換条件の定理の証明
ルベーグの収束定理はルベーグ測度空間でなくとも,任意の測度空間上でも同様に成り立ちます.
計数測度空間$(\mathbb{N},2^{\mathbb{N}},\mu)$における積分は和になるのでしたから,ルベーグの収束定理は極限と級数の順序交換可能であるための条件になります.
[極限と級数の順序交換条件(再掲)]$I\subset\R$を開集合とし,$a\in I$と,$I$上の実数値関数列$\{f_n\}_{n\in\N}$を考える.任意の$n\in\N$に対して,極限$\lim_{x\to a}f_n(x)$は収束するとする.このとき,ある実数列$\{M_n\}$が存在して,
- 任意の$x\in I$に対し$|f_n(x)|\le M_n$
- $\{M_n\}$は総和可能:$\sum_{n=1}^{\infty}M_n<\infty$
を満たすなら,
\begin{align*}\lim_{x\to a}\sum_{n=1}^{\infty}f_n(x)=\sum_{n=1}^{\infty}\lim_{x\to a}f_n(x)\end{align*}
が成り立つ.
定理の仮定より
- 任意の$n\in\N$に対して極限$\lim_{x\to a}f_n(x)$が収束する
- 任意の$x\in I$に対し$|f_n(x)|\le M_n$($n\in\N$)を満たす
が成り立つ.
計数測度空間$(\N,2^{\N},\mu)$において,$\N$は可測集合であり,全ての$n\in\N$に対して$M_n\ge0$だから
\begin{align*}\sum_{n=1}^{\infty}M_n=\sum_{n\in\N}M_n=\int_{\N}M_n\,d\mu(n)\end{align*}
となり,定理の仮定と併せて$\int_{\N}M_n\,d\mu(n)=\sum_{n=1}^{\infty}M_n<\infty$が成り立つ.
よって,$\N$上でルベーグの収束定理を適用できて
\begin{align*}\lim_{t\to a}\int_{\N}f_n(x)\,d\mu(n)=\int_{\N}\lim_{t\to a}f_n(x)\,d\mu(n)\end{align*}
が成り立つ.すなわち,
\begin{align*}\lim_{t\to a}\sum_{n=1}^{\infty}f_n(x)=\sum_{n=1}^{\infty}\lim_{t\to a}f_n(x)\end{align*}
が成り立つ.
通常の(ルベーグ測度空間での)ルベーグの収束定理と,いまの計数測度空間でのルベーグの収束定理で,次のように対応していることを意識すると理解しやすいでしょう.
| 測度空間 | ルベーグ測度空間 | 計数測度空間 |
|---|---|---|
| 関数 | $f_t(x)$ | $f_n(x)$ |
| 測度空間の変数 | $x$ | $n$ |
| 極限をとる変数 (パラメータ) |
$t$ | $x$ |
| 優関数 | $t$によらない関数$g(x)$ | $x$によらない実数列$\{M_n\}$ |
微分と級数の順序交換可能な条件
通常の(ルベーグ測度空間での)ルベーグの収束定理の応用として,微分とルベーグ積分の順序交換ができるための条件を導くことができます.
計数測度空間$(\N,2^{\N},\mu)$上でも同様に議論を進めることで,次の微分と級数の順序交換ができるための条件を導くことができます.
[微分と級数の順序交換条件(再掲)]$I\subset\R$を開集合とし,$I$上の実数値関数列$\{f_n\}_{n\in\N}$を考える.任意の$n\in\N$に対して,$f_n$は$I$上微分可能であるとする.任意の$x\in I$に対して,実数列$\{f_n(x)\}_n$の級数は収束するとし
\begin{align*}F(x)=\sum_{n=1}^{\infty}f_n(x)\end{align*}
とおく.このとき,ある実数列$\{M_n\}$が存在して,
- 任意の$n\in\N$と$x\in I$に対して$|{f_n}'(x)|\le M_n$
- $\{M_n\}$は総和可能:$\sum_{n=1}^{\infty}M_n<\infty$
を満たすなら,$F$は$I$上微分可能で
\begin{align*}F'(x)=\sum_{n=1}^{\infty}{f_n}'(x)\end{align*}
が成り立つ.
任意に$x\in I$をとる.$f_n$は微分可能だから
\begin{align*}\lim_{h\to0}\frac{f_n(x+h)-f_n(x)}{h}={f_n}'(x)\end{align*}
が存在する.$x+h\in I$となる任意の$h\in\R$に対して,平均値の定理より,ある$\theta\in(0,1)$が存在して
\begin{align*}\abs{\frac{f_n(x+h)-f_n(x)}{h}}=\abs{{f_n}'(x+\theta h)}\le M_n\end{align*}
が成り立つ.仮定より$M_n$は総和可能だから,[極限と級数の順序交換条件]の定理が適用できて
\begin{align*}F'(x)&=\lim_{h\to0}\frac{\sum_{n=1}^{\infty}f_n(x+h)-\sum_{n=1}^{\infty}f_n(x)}{h}
\\&=\lim_{h\to0}\sum_{n=1}^{\infty}\frac{f_n(x+h)-f_n(x)}{h}
=\sum_{n=1}^{\infty}{f_n}'(x)\end{align*}
が成り立つ.
証明から分かるように,被積分関数の絶対値$\abs{\frac{f_n(x+h)-f_n(x)}{h}}$を評価するために平均値の定理を使うので,導関数の絶対値$|{f_n}'(x)|$を上から押さえる総和可能な実数列$\{M_n\}$が存在すれば良いわけですね.

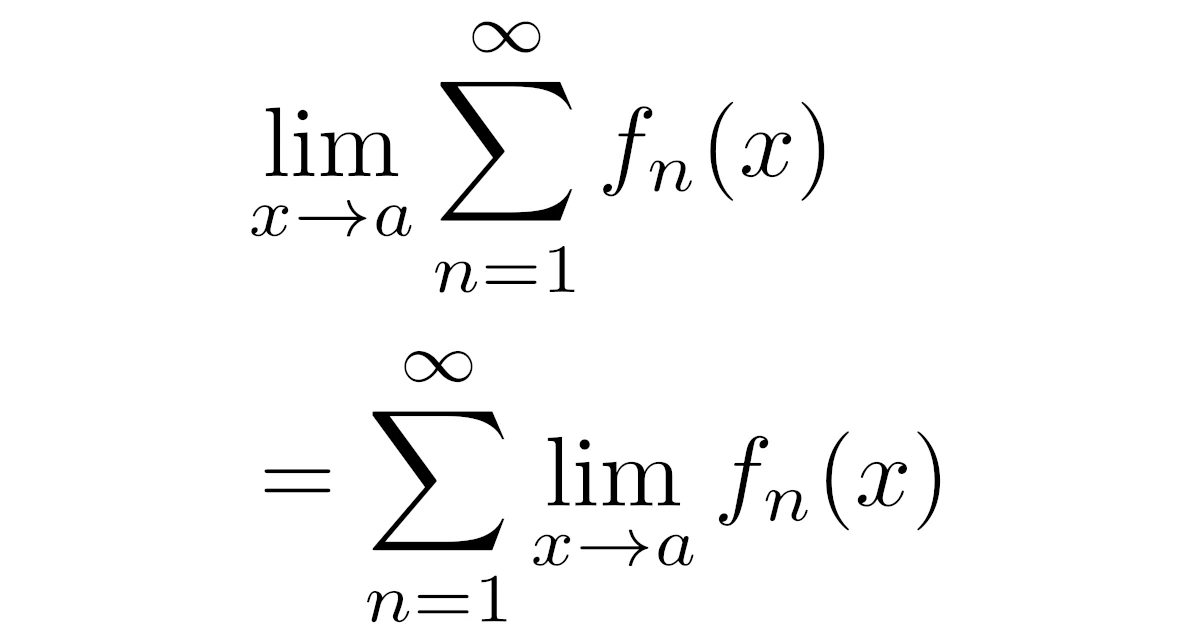
コメント