ルベーグ外測度$m^{*}$はほとんど「集合の長さを測る写像」と言えるのですが，次のような不都合があるのでした．
$A\cap B=\emptyset$かつ$m^{*}(A\cap B)\neq m^{*}(A)+m^{*}(B)$を満たす$A,B\subset\R$が存在する．
つまり，２つの集合の共通部分が空であっても，和集合のルベーグ外測度$m^{*}(A\cap B)$とルベーグ外測度の和$m^{*}(A)+m^{*}(B)$が一致しないことがあるわけですね．
結論から言えば，ルベーグ外測度$m^{*}$の定義域をルベーグ可測集合と呼ばれる集合たちに制限すると，この不都合が解消されます．この定義域を制限してできる写像$m$をルベーグ測度といいます．
この記事では
- 完全加法性（$\sigma$-加法性）とルベーグ外測度の欠点
- ルベーグ可測集合の定義・必要十分条件・具体例
- ルベーグ測度の定義と完全加法性
を順に説明します．
以下ではルベーグ外測度を$m^{*}$で表し，単に「外測度」と呼びます．また，右半開区間$I=[a,b)$の長さ$b-a$を$|I|$と表します．
「ルベーグ積分の基本」の一連の記事
- ルベーグ積分入門
- ルベーグ測度
- ルベーグ可測関数とルベーグ積分
ルベーグ積分の参考文献
以下はルベーグ積分に関するオススメの教科書です．
ルベグ積分入門
ロングセラーの入門書です．専門書ですが，文庫なので安く購入できるのも魅力です．
ルベーグ積分と関数解析
ルベーグ積分から更なるステップに進みたい人向けの教科書です．
完全加法性（$\sigma$-加法性）とルベーグ外測度の欠点
もし写像$m$が集合の「長さ」を測るのであれば，直感的には次の性質$(*)$は満たしておいて欲しいですね．
$(*)$：$A_1, A_2,\dots$が互いに素（$i\neq j$なら$A_i\cap A_j=\emptyset$）なら$m\biggl(\bigcup\limits_{n=1}^{\infty}A_n\biggr)=\sum\limits_{n=1}^{\infty}m(A_n)$が成り立つ．
この性質$(*)$は一般の測度論でも本質的に重要な性質で$m$の完全加法性や$\sigma$-加法性などと呼ばれます．
ここで，外測度$m^{*}$が単調性・劣加法性を満たすことを思い出しておきましょう．
ルベーグ外測度$m^{*}$は次の性質を満たす．
完全加法性$(*)$を満たす写像$m$を考えると，
- ［単調性］$A\subset B$なる集合$A,B\subset\R$は$m(A)\le m(B)$を満たす
- ［劣加法性］集合$A_1, A_2,\dots\subset\R$は$m\biggl(\bigcup\limits_{n=1}^{\infty}A_n\biggr)\le\sum\limits_{n=1}^{\infty}m(A_n)$を満たす
が成り立つことは証明できます．
しかし，逆に単調性と劣加法性が成り立っても完全加法性が成り立つとは限らず，実際に外測度$m^{*}$は上の完全加法性$(*)$に対応する性質を満たしません（このことは冒頭の不具合から分かります）．
ルベーグ積分（測度論）では完全加法性$(*)$が重要なため，外測度$m^{*}$が完全加法性を満たしていないことは致命的な欠点となります．
ルベーグ可測集合の定義・必要十分条件・具体例
外測度$m^{*}$の定義域である$\R$の冪集合$\mathcal{P}(\R)$を少し狭めることで，完全加法性$(*)$を獲得させることを考えます．
$\R$の冪集合$\mathcal{P}(\R)$とは，$\R$の部分集合全部の集合のことでした．
ルベーグ可測集合の定義
ここでルベーグ可測集合を定義します．
集合$A\subset\R$がルベーグ可測集合（Lebesgue measurable set）または単に可測集合であるとは，任意の$X\subset\R$に対して
\begin{align*}m^{*}(X)=m^{*}(X\cap A)+m^{*}(X\cap A^c)\quad\dots(**)\end{align*}
を満たすことをいう．ここに，$A^c$は$\R$における$A$の補集合である．
この「任意の$X\subset\R$に対して条件$(**)$を満たす」という$A\subset\R$の条件をカラテオドリー（Carathéodory）の条件という．
また，ルベーグ可測集合全部の族をルベーグ可測集合族という．
集合としては
\begin{align*}X=(X\cap A)\cup(X\cap A^c)\end{align*}
が成り立ちます．この右辺は直和なので，どんな$A$, $X$に対してもカラテオドリーの条件
\begin{align*}m^{*}(X)=m^{*}(X\cap A)+m^{*}(X\cap A^c)\end{align*}
が成り立ちそうに思えるかもしれません．
しかし，この記事の冒頭で不具合として紹介したように，実はヘンテコな集合$A$に対しては$(**)$を満たさない$X$が存在します．つまり，ルベーグ可測集合でない集合が存在します．
詳しくは後述しますが，実は外測度$m^{*}$の定義域をルベーグ可測集合全体に制限してできる写像$m$は完全加法性$(*)$を満たすことが証明でき，こうしてできる写像$m$をルベーグ測度と定義します．
のちの記事で証明するように，開集合や閉集合は可測集合であり，可測集合の和集合や共通部分も可測集合となります．このことから，ルベーグ非可測集合はそれなりに変なことをしないと簡単には作れそうにないことが分かりますね．
ルベーグ可測集合であるための必要十分条件
ルベーグ可測集合の具体例を考える前に，ルベーグ可測集合であるための必要十分条件を与えておきます．
外測度$m^{*}$は劣加法性を満たすので，常に
\begin{align*}m^{*}(X\cap A)+m^{*}(X\cap A^c)
&\ge m^{*}((X\cap A)\cup(X\cap A^c))
\\&=m^{*}(X\cap(A\cup A^c))
\\&=m^{*}(X\cap\R)
=m^{*}(X)\end{align*}
が成り立ちます．すなわち，ルベーグ可測集合の定義の条件式$(*)$の$\le$は常に成り立ちます．
そのため，ルベーグ可測集合であるためには逆向きの不等式$m^{*}(X)\ge m^{*}(X\cap A)+m^{*}(X\cap A^c)$を示せば十分ですね．
さらに，$m^{*}(X)=\infty$なら$\ge$は常に成り立ちますから，次が成り立ちますね．
集合$A\subset\R$に対して，次は同値である．
- $A$はルベーグ可測集合である．
- $m^{*}(X)<\infty$なる任意の$X\subset\R$に対して$m^{*}(X)\ge m^{*}(X\cap A)+m^{*}(X\cap A^c)$が成り立つ．
ルベーグ可測集合の具体例をいくつか見てみましょう．
具体例１（$\R$の可測性）
$\R$がルベーグ可測集合であることを示せ．
上の命題より$m^{*}(X)\ge m^{*}(X\cap \R)+m^{*}(X\cap \R^c)$を示せば十分ですが，簡単に等号$=$まで示せるので等号$=$まで示しましょう．
任意の集合$X\subset\R$に対して
\begin{align*}m^{*}(X)=m^{*}(X\cap \R)+m^{*}(X\cap \R^c)\end{align*}
が成り立つことを示せばよい．
$X\subset\R$より$X\cap\R=X$, $X\cap \R^c=X\cap\emptyset=\emptyset$であり，外測度$m^{*}$の性質$m^{*}(\emptyset)=0$を併せると
\begin{align*}m^{*}(X\cap \R)+m^{*}(X\cap \R^c)=m^{*}(X)+m^{*}(\emptyset)=m^{*}(X)\end{align*}
が成り立つので，$\R$はルベーグ可測集合である．
具体例２（ルベーグ零集合の可測性）
$A\subset\R$が$m^{*}(A)=0$を満たすとき，$A$がルベーグ可測集合であることを示せ．
上の命題より$m^{*}(X)\ge m^{*}(X\cap \R)+m^{*}(X\cap \R^c)$を示せば十分ですね．
任意の集合$X\subset\R$に対して
\begin{align*}m^{*}(X)\ge m^{*}(X\cap A)+m^{*}(X\cap A^c)\quad\dots(*)\end{align*}
が成り立つことを示せばよい．
$X\cap A\subset A$, $X\cap A^c\subset X$だから，外測度$m^{*}$の単調性より
\begin{align*}&m^{*}(X\cap A)\le m^{*}(A)=0,
\\&m^{*}(X\cap A^c)\le m^{*}(X)\end{align*}
が成り立つ．よって，辺々足し合わせて$(*)$が成り立つから$A$はルベーグ可測集合である．
$A\subset\R$が$m^{*}(A)=0$を満たすとき，$A$はルベーグ零集合であるといいます．よって，いまの例は次のようにいうことができますね．
ルベーグ零集合はルベーグ可測集合である．
さらに，一般に可算集合はルベーグ零集合でしたから，さらに次の系も当たり前にしておきましょう．
可算集合はルベーグ可測集合である．
正の整数全部の集合$\N$や有理数全部の集合$\Q$は可算集合でしたから，$\N$も$\Q$もルベーグ可測集合と言えるわけですね．
ルベーグ測度の定義と完全加法性
先ほど簡単に説明したように，外測度の定義域をルベーグ可測集合たちに制限したものをルベーグ測度といいます．
外測度$m^{*}$の定義域をルベーグ可測集合族$\mathcal{L}$に制限してできる写像$m=m^{*}|_{\mathcal{L}}$をルベーグ測度（Lebesgue measure）という．
また，ルベーグ可測集合$A$に対して$m(A)$を$A$の測度（measure）という．
一般に$X\subset Y$なる集合$X$, $Y$と$Y$を定義域とする写像$f$に対して，$f$の定義域を$X$に制限してできる写像を$f|_{X}$と表します．
定義域が異なる写像は異なる写像とみなすので，$f$と$f|_{X}$は異なる写像です．よって，ルベーグ外測度$m^{*}$とルベーグ測度$m$は異なる写像です．
ルベーグ測度$m$は次のように完全加法性$(*)$を満たします．
ルベーグ測度$m$と$A_1, A_2,\dots\in\mathcal{L}$を考える．このとき，$\bigcup\limits_{n=1}^{\infty}A_n\in\mathcal{L}$であり，$A_1, A_2,\dots$のどの２つの共通部分も空集合なら
\begin{align*}m\bra{\bigcup_{n=1}^{\infty}A_n}=\sum\limits_{n=1}^{\infty}m(A_n)\quad\dots(*)\end{align*}
が成り立つ．
ただし，この完全加法性を証明するには，ルベーグ可測集合の性質について理解しておく必要があるため，証明はのちの記事で行います．
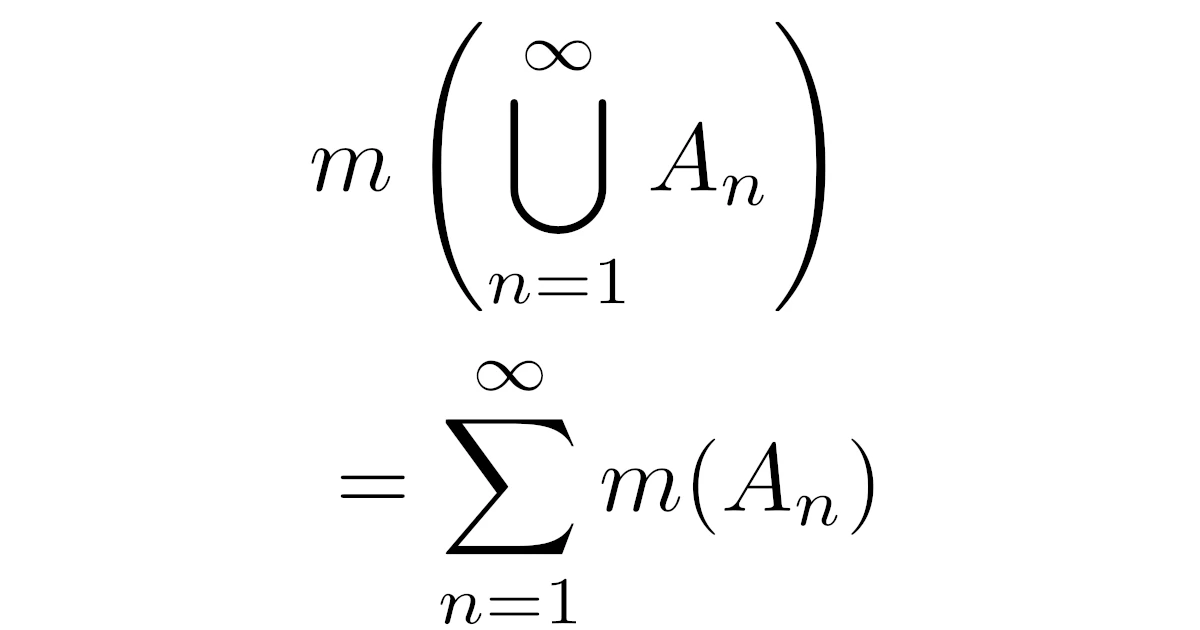
コメント