ルベーグ測度$m$はルベーグ積分において本質的に重要なので，ルベーグ測度$m$の性質を理解しておくことは大切です．
ルベーグ外測度$m^{*}$は５つの性質を持ちましたが，完全加法性を満たさないため測度論の観点からは十分よい性質をもつとは言えないのでした．
一方，ルベーグ外測度$m^{*}$の定義域をルベーグ可測集合族$\mathcal{L}$に制限することで，ルベーグ測度$m$はルベーグ外測度$m^{*}$よりも良い性質をもちます．
そこで，この記事では
- ルベーグ測度$m$の４つの重要性質
- 完全加法性の証明
を順に説明します．
「ルベーグ積分の基本」の一連の記事
- ルベーグ積分入門
- ルベーグ測度
- ルベーグ可測関数とルベーグ積分
ルベーグ積分の参考文献
以下はルベーグ積分に関するオススメの教科書です．
ルベグ積分入門
ロングセラーの入門書です．専門書ですが，文庫なので安く購入できるのも魅力です．
ルベーグ積分と関数解析
ルベーグ積分から更なるステップに進みたい人向けの教科書です．
ルベーグ測度$m$の４つの重要性質
外測度$m^{*}$の５つの性質を復習してから，ルベーグ測度$m$の性質を説明します．
ルベーグ外測度$m^{*}$の性質と欠点
ルベーグ外測度$m^{*}$は次の５つの性質を満たす．
- ［非負値性］任意の集合$A\subset\R$は$m^{*}(A)\ge0$を満たす．また，$m^{*}(\emptyset)=0$が成り立つ．
- ［平行移動不変性］平行移動で移り合う集合$A, B\subset\R$は$m^{*}(A)=m^{*}(B)$を満たす．
- ［単調性］$A\subset B$を満たす集合$A, B\subset\R$は$m^{*}(A)\le m^{*}(B)$を満たす．
- ［劣加法性］集合$A_1, A_2,\dots\subset\R$は$m^{*}\bra{\bigcup\limits_{n=1}^{\infty}A_n}\le\sum\limits_{n=1}^{\infty}m^{*}(A_n)$を満たす．
- ［区間の外測度］右半開区間$I\subset\R$は$m^{*}(I)=|I|$を満たす．
ルベーグ測度$m$は外測度$m^{*}$の定義域をルベーグ可測集合族$\mathcal{L}$に制限してできるものでしたから，これらの性質は全て引き継がれますね．
しかし，外測度$m^{*}$について次のような集合が存在し，この事実が測度論における外測度$m^{*}$の致命的な欠点になっています．
$A\cap B=\emptyset$かつ$m^{*}(A\cap B)\neq m^{*}(A)+m^{*}(B)$を満たす$A,B\subset\R$が存在する．
この命題の集合$A$, $B$の存在はヴィタリ集合という集合を考えることで証明できますが，ヴィタリ集合はそう簡単な集合ではありません．いまは「外測度$m^{*}$の不具合がルベーグ測度では解消されている」という認識で問題ありません．
ルベーグ測度$m$の性質
ルベーグ測度$m$は外測度$m^{*}$にはない次の完全加法性を満たします．
［完全加法性］互いに素な可測集合$A_1, A_2,\dots$は$m\bra{\bigcup\limits_{n=1}^{\infty}A_n}=\sum\limits_{n=1}^{\infty}m(A_n)$を満たす．
外測度$m^{*}$がこの性質を満たさないことは上の命題から分かりますね．
$m$で「長さ」が測る集合は可測集合のみなので，左辺では$\bigcup\limits_{n=1}^{\infty}A_n$が可測集合でなければなりませんが，以前の記事で$A_1,A_2,\dots$が可測集合なら$\bigcup\limits_{n=1}^{\infty}A_n$も可測集合であることを証明していたので問題ありませんね．
ルベーグ測度$m$の完全加法性から単調性と劣加法性が証明できるので，上で見た外測度の５つの性質と完全加法性を併せて，ルベーグ測度$m$の性質は次の４性質にまとめることができますね．
ルベーグ測度$m$は次の４つの性質を満たす．
- ［非負値性］任意の可測集合$A\subset\R$は$m^{*}(A)\ge0$を満たす．また，$m^{*}(\emptyset)=0$が成り立つ．
- ［平行移動不変性］平行移動で移り合う可測集合$A, B$は$m^{*}(A)=m^{*}(B)$を満たす．
- ［完全加法性］互いに素な可測集合$A_1, A_2,\dots$に対して$m\bra{\bigcup\limits_{n=1}^{\infty}A_n}=\sum\limits_{n=1}^{\infty}m(A_n)$が成り立つ．
- ［区間の外測度］右半開区間$I\subset\R$は$m^{*}(I)=|I|$を満たす．
ルベーグ測度$m$の完全加法性と測度空間
それではルベーグ測度$m$の完全加法性を証明しましょう．
$m$の完全加法性の証明
ルベーグ測度$m$の完全加法性の証明のために，以前の記事で証明した次の補題を思い出しておきましょう．
可測集合$A_1,A_2,\dots$が互いに素なら，任意の$X\subset\R$と$n\in\N$に対して
\begin{align*}m^{*}(X\cap B_n)=\sum_{k=1}^{n}m^{*}(X\cap A_k)\end{align*}
が成り立つ．ただし，$B_n=\bigcup\limits_{k=1}^{n}A_k$ ($n\in\N$)である．
この補題を用いて$m$の完全加法性を示しましょう．
［完全加法性（再掲）］互いに素な集合$A_1, A_2,\dots\in\mathcal{L}$に対して$m\bra{\bigcup\limits_{n=1}^{\infty}A_n}=\sum\limits_{n=1}^{\infty}m(A_n)$が成り立つ．
$A=\bigcup\limits_{n=1}^{\infty}A_n$, $B_n=\bigcup\limits_{k=1}^{n}A_k$とする．$m^{*}$の劣加法性より
\begin{align*}m^{*}(A)
=m^{*}\bra{\bigcup_{n=1}^{\infty}A_n}
\le\sum_{n=1}^{\infty}m^{*}(A_n)\end{align*}
が成り立つから，逆向きの不等式$m^{*}(A)\ge\sum_{n=1}^{\infty}m^{*}(A_n)$を示せば良い．
$B_n\in\mathcal{L}$だから，任意の$X\subset\R$に対して
\begin{align*}m^{*}(X)=m^{*}(X\cap B_n)+m^{*}(X\cap B_n^c)\end{align*}
が成り立つから，補題を第１項目に用いると，
\begin{align*}m^{*}(X)=\sum_{k=1}^{n}m^{*}(X\cap A_k)+m^{*}(X\cap B_n^c)\end{align*}
が成り立つ．ここで$X=A$とすると，
\begin{align*}m^{*}(A)
=&\sum_{k=1}^{n}m^{*}(A\cap A_k)+m^{*}(A\cap B_n^c)
\\\ge&\sum_{k=1}^{n}m^{*}(A_k)\end{align*}
が成り立つ．よって，$n\to\infty$とすれば$m^{*}(A)\ge\sum\limits_{n=1}^{\infty}m^{*}(A_n)$が成り立つ．
ルベーグ測度空間
$\R$上のルベーグ可測集合族$\mathcal{L}$は完全加法族でしたから，$(\R,\mathcal{L})$は可測空間となるのでした．
測度論の基本的な空間として測度空間が次のように定義されます．
可測空間$(\Omega,\mathcal{F})$を考える．写像$\mu:\mathcal{F}\to[0,\infty]$が次を満たすとき，$\mu$を測度（measure）といい，組$(\Omega,\mathcal{F},\mu)$を測度空間（measure space）という．
- $\mu(\emptyset)=0$
- 互いに素な$A_1,A_2,\dots\in\mathcal{F}$に対して$\mu\bra{\bigcup\limits_{n=1}^{\infty}A_n}=\sum\limits_{n=1}^{\infty}\mu(A_n)$が成り立つ．
つまり，可測空間$(\Omega,\mathcal{F})$の$\mathcal{F}$に属する集合の「元の多さ」を定量的に測ってくれるものを測度$\mu$として定義したわけですね．
この記事で示したように，可測空間$(\R,\mathcal{L})$に対してルベーグ測度$m$はこの定義の条件を満たしていますね．
すなわち，$(\R,\mathcal{L},m)$は測度空間となっており，この測度空間$(\R,\mathcal{L},m)$をルベーグ測度空間（Lebesgue measure space）といい，ルベーグ積分はこのルベーグ測度空間上で考える積分となっています．
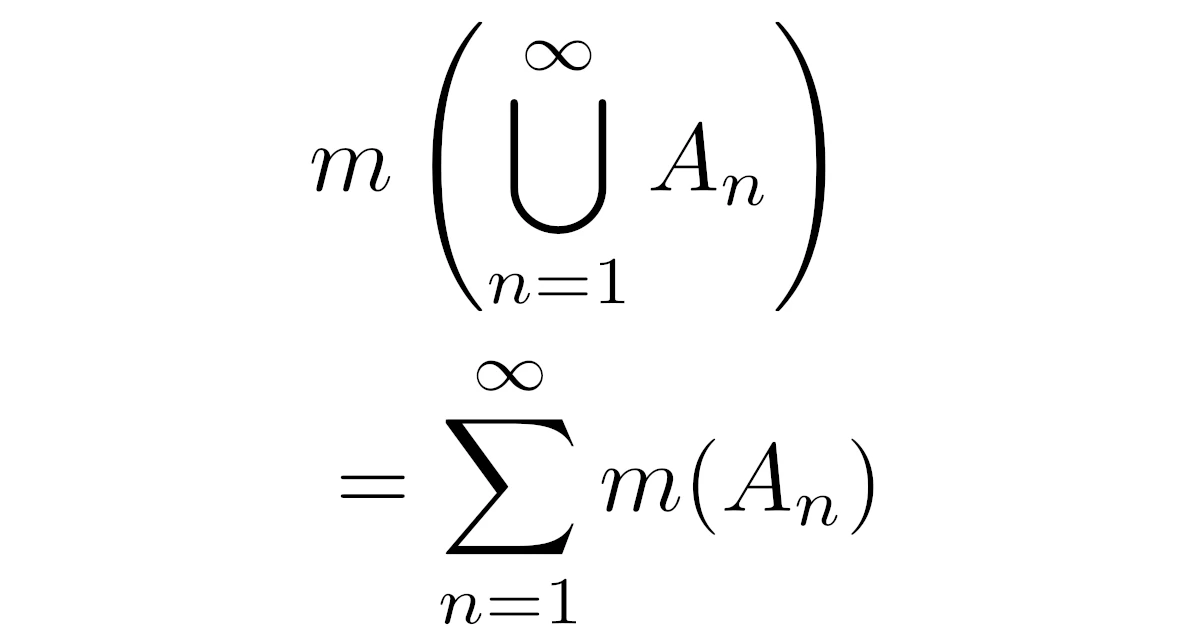
コメント