位相空間$X$において「集合$A\subset X$がひとまとまりになっていること」を表す概念として連結性があります.
大雑把に言えば「集合$A$が2つの開集合によって分けられない」とき,集合$A$は連結であるといいます.
似た概念に弧状連結性がありますが,実は「弧状連結なら連結」は成り立ちますが逆は成り立ちません.つまり,連結性の方が少し広い性質となっています.
この記事では
- 連結性の定義と具体例
- 連結性と弧状連結性の関係
- 参考文献
を順に解説します.
なお,この記事では$X$を位相空間とします.
位相空間をよく知らない方は$X$をユークリッド空間$\R$, $\R^2$(数直線,$xy$平面)と思って読み進めても内容は理解できます.
連結性の定義と具体例
連結性を定義して具体例を考えましょう.
2つの開集合で分けられない集合を連結という
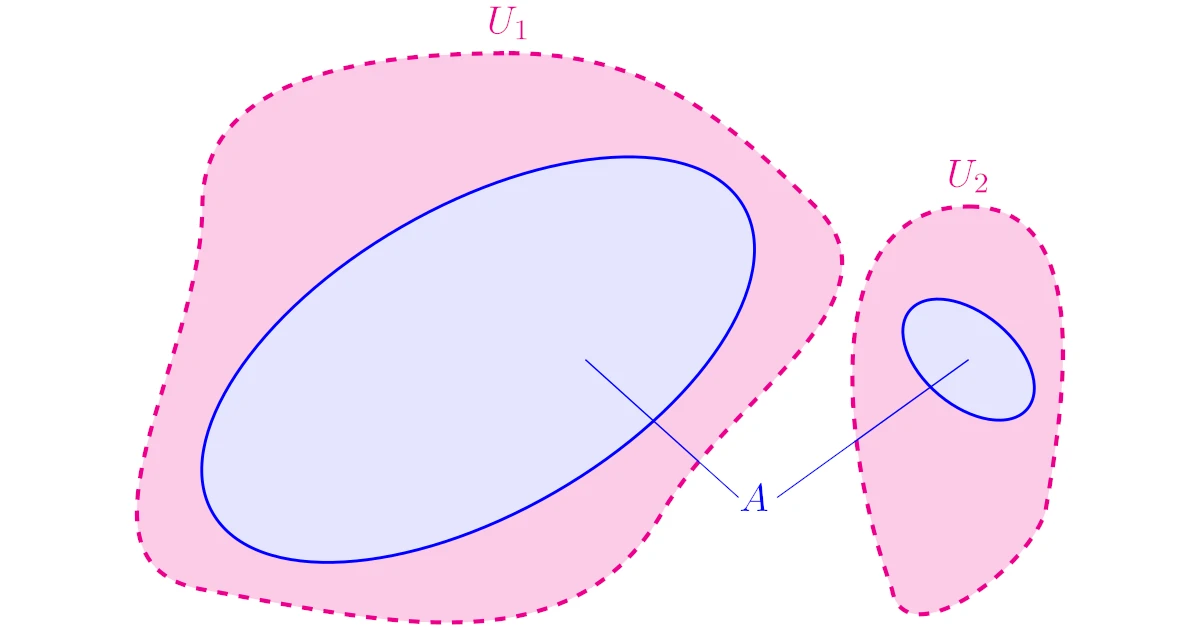
集合$A\subset X$が連結であるとは,3つの条件
- $A\subset U_1\cup U_2$
- $U_1\cap U_2=\emptyset$
- $A\cap U_{i}\neq\emptyset$($i=1,2$)
を満たす$X$上の開集合$U_1$, $U_2$が存在しないことをいう.
3つの条件を満たす$X$上の開集合$U_1$, $U_2$が存在するときは非連結であるという.
もし「離れ小島」があれば,異なる「島」は2つの開集合で分けられますから,集合$A$は「ひとまとまり」とは言えないというイメージですね.
このような2つの開集合$U_1$, $U_2$が存在しないとき,集合$A$は連結であるというわけですね.
連結開集合を領域という
数学ではよく領域という言葉が使われますが,これは次のように定義されます.
集合$A\subset X$が領域であるとは,$A$が連結な開集合であることをいう.
高校数学では「軌跡と領域」の分野で「ベタッと塗りつぶせるような集合」をざっくり領域と呼ぶことが多かったと思いますが,大学以降の数学で領域というとこの定義の通り連結な開集合のことを指すことが多いです.
大学以降の数学でも誤解が生じないときは深く考えず「ベタッと塗りつぶせるような集合」を領域と呼ぶこともなくはありませんが,話し手も聞き手も注意が必要です.
具体例1(連結な集合)
集合$[0,1]\subset\R$は連結であることを示せ.ただし,$\R$は1次元ユークリッド空間(通常の数直線)とする.
背理法により示す.すなわち,$I:=[0,1]$が連結でないと仮定して矛盾を導く.$I:=[0,1]$が連結でないなら,
\begin{align*}&I\subset U_1\cup U_2,\quad
U_1\cap U_2=\emptyset,
\\&I\cap U_i\neq\emptyset\quad (i=1,2)\end{align*}
を満たす$\R$上の開集合$U_1$, $U_2$が存在する.
$U_1$, $U_2$は対称なので$1\in U_2$としてよく,このときある$\epsilon>0$が存在して$(1-\epsilon,1]\subset U_2$が成り立つ.$a:=\sup{(I\cap U_1)}$とおくと,$U_1\cap U_2=\emptyset$と併せて$a\le1-\epsilon<1$である.
$U_1$は開集合だから$a\not\in U_1$であり,$I\subset U_1\cup U_2$と併せると$a\in U_2$である.
$U_2$は開集合だから$a$のある近傍$U$が存在して$U\subset U_2$となるが,$a=\sup{(I\cap U_1)}$より$U\cap U_1\neq\emptyset$となって$U_1\cap U_2=\emptyset$に矛盾する.
一般に$\R$上の任意の区間は連結となります.
このことから,$\R$上の区間を$\R$の連結部分集合と定義することもあります.
具体例2(連結でない集合)
$\R^2$を2次元ユークリッド空間(通常の$xy$平面)とする.$A\subset\R^2$を
\begin{align*}A=\set{\bmat{x\\0}\in\R^2}{x\neq0}\end{align*}
とすると,$A$が連結でないことを示せ.
$A$は$x$軸から原点を除いた集合ですね.
$U_i\subset\R^2$($i=1,2$)を
\begin{align*}U_1=\set{\bmat{x\\y}\in\R^2}{x>0},\quad
U_2=\set{\bmat{x\\y}\in\R^2}{x<0}\end{align*}
で定める.
このとき,
\begin{align*}&A\subset U_1\cup U_2,\quad
U_1\cap U_2=\emptyset,
\\&A\cap U_i\neq\emptyset\quad (i=1,2)\end{align*}
を満たすので,$A$は連結でない.
連結性と弧状連結性の関係
連結性の基本的な性質をいくつか解説します.
連結な集合の連続写像による像も連結
直観的には,連続写像は集合の「つながり方」を保存するので,連結性も保存しそうですね.
$X$, $Y$を位相空間とし,$f:X\to Y$を連続写像とし,$A\subset X$とする.$A$が$X$上で連結なら,$f(A)$は$Y$上で連結である.
対偶を示す.$f(A)$は$Y$上で連結でないと仮定する.このとき,
\begin{align*}&f(A)\subset U_1\cup U_2,\quad
U_1\cap U_2=\emptyset,
\\&f(A)\cap U_i\neq\emptyset\quad (i=1,2)\end{align*}
なる$Y$上の開集合$U_1,U_2$が存在する.このとき,$V_i:=f^{-1}(U_i)$を定めると,$f$の連続性より$V_i$は開集合であり($i=1,2$),
- $A\subset f^{-1}(f(A))\subset f^{-1}(U_1\cup U_2)=V_1\cup V_2$
- $V_1\cap V_2=f^{-1}(U_1\cap U_2)=f^{-1}(\emptyset)=\emptyset$
- $b\in f(A)\cap U_i$をとると,ある$a\in A$が存在して$f(a)=b\in U_i$だから$a\in V_i$が得られ,$A\cap V_i\neq\emptyset$
が成り立つ.よって,$A$は連結でないことが分かり,これで対偶が示された.
$A\subset f^{-1}(f(A))$であり,等号が成り立つとは限らないことに注意してください.
連結性は弧状連結より広い概念
弧状連結なら連結であることを証明しましょう.上で示した命題を使いましょう.
$A\subset X$とする.$A$が弧状連結なら,$A$は連結である.
背理法により示す.弧状連結な$A$が連結でないと仮定する.このとき,
\begin{align*}&A\subset U_1\cup U_2,\quad
U_1\cap U_2=\emptyset,
\\&A\cap U_i\neq\emptyset\quad (i=1,2)\end{align*}
なる開集合$U_1,U_2\subset X$が存在する.
このとき,任意の$a\in A\cap U_1$, $b\in A\cap U_2$に対して,$a,b\in A$だから$A$の弧状連結性より$f(0)=a$, $f(1)=b$なる連続曲線$f:[0,1]\to A$が存在する.
具体例1より1次元ユークリッド空間$\R$上で$[0,1]$は連結だったから,上の命題と併せて$f([0,1])\subset A$は連結となるが,
\begin{align*}&f([0,1])\subset A\subset U_1\cup U_2,
\\&U_1\cap U_2=\emptyset,
\\&f([0,1])\cap U_i\neq\emptyset\quad (i=1,2)\end{align*}
となって矛盾する.
要は「2つの空でない開集合$U_1$, $U_2$で$A$を分割できるなら,2点$a\in U_1$, $b\in U_2$を$A$上の曲線で結ぶことはできない」ということを証明したわけですね.
これも冒頭で説明したように,この逆は成り立ちません.つまり,連結であっても弧状連結であるとは限りません.
この「連結であるが弧状連結ではない集合」の具体例は以下の記事を参照してください.
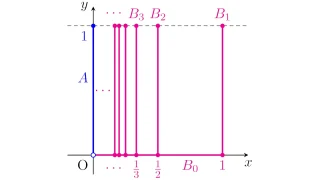
参考文献
集合・位相入門
[松坂和夫 著/岩波書店]
本書は「集合論」「位相空間論」をこれから学ぶ人のための入門書です.
本書は説明が丁寧で行間が少ないテキストなので,初学者にとっても読みやすくなっています.
実際,本書は1968年に発刊されて以来売れ続けている超ロングセラーで,2018年に新装版が発売されたことからも現在でも広く使われていることが分かります.
具体例が多く扱われているのも特徴で,新しい概念のイメージも掴みやすいように書かれています.
また,各セクションの終わりに少なくない数の演習問題も載っており,演習書的な使い方もできます.
なお,本書については,以下の記事で書評としてまとめています.
【オススメの教科書|集合・位相入門(松坂和夫著,岩波書店)】
本書の目次・必要な知識・良い点と気になる点・オススメの使い方などをレビューしています.
集合と位相
[鎌田正良 著/近代科学社(現代数学ゼミナール)]
本書はすっきりと書かれた「集合論」「位相空間論」の教科書です.
簡潔な説明が多いので,集合と位相の基本の全体像をさらうのに適しています.
裏返せば簡潔すぎてかえって分かりにくい可能性もありますが,数学をきちんと学びたい人には是非読みこなして欲しいテキストです.
また,演習問題の解説も丁寧に書かれているので,この点は独学で学ぶ場合には重宝します.
背景にある位相の圏論的な性質も踏まえて解説されており,数学系の学生は是非とも理解しておきたい考え方です.



コメント