代数学は数学の構造を考える分野であり,群・環・体は代数学における基本的な概念です.
この群・環・体といった代数構造を定義するためには集合と2項演算が必要で,例えば
- 「整数の集合$\Z$」は「通常の加法+」によって群
- 「実数係数の1変数多項式の集合$\R[x]$」は「通常の加法+と乗法・」によって環
- 「実数の集合$\R$」は「通常の加法+と乗法・」によって体
となります.
この記事では,
- 二項演算とは何か?
- 群の定義と具体例
- 環の定義と具体例
- 体の定義と具体例
を順に説明します.
二項演算とは何か?
まずは群・環・体を定義するために欠かせない二項演算がどういうものか説明します.
二項演算とは2つの元から1つの元をつくる規則
例えば,整数の足し算や掛け算は
\begin{align*}2+3=5,\quad 2\cdot3=6\end{align*}
のように「2つの実数」から新たな「1つの実数」を生み出すものとなっています.
この足し算や掛け算は実数上の二項演算の1つで,一般に集合$A$上の二項演算は次で定義されます.
[二項演算]集合$A$に対して,写像$f:A\times A\to A$を$A$上の二項演算または単に演算という.
また「演算を$\star$とする」と書いた場合は,$a,b\in A$の$\star$による演算を$a\star b$と表す.
$a\star b$という記法は足し算を$a+b$で表したり,掛け算を$a\times b$で表すのと同じ気持ちです.
2つの元$a,b\in A$に対して,行き先が$A$上に1つに決まればそれだけで演算というわけですから,演算は無数に考えられますね.例えば,任意の$a,b\in\R$に対して
- $f(a,b)=ab$
- $f(a,b)=a+4b$
- $f(a,b)=b\sin^3{a}$
で定まる$f:\R\times\R\to\R$はいずれも$\R$上の演算です.
$\R$は実数全部の集合を指します.そのため,「$a,b\in\R$に対して」は「実数$a$, $b$に対して」と同じ意味です.
もちろん無茶苦茶な演算を考えることもできるので,演算は必ずしも「良い性質」をみたすとは限りません.そのため代数学ではある程度「良い性質」をもった演算が定まっている集合を考えます.
2項演算に関する3法則
いま「良い性質」と書きましたが,ここで「良い性質」とは結合法則・交換法則・分配法則のことを指しています.
[結合法則]集合$A$に演算$\star$が定まっているとする.このとき,任意の$a,b,c\in A$に対して,
\begin{align*}(a\star b)\star c=a\star (b\star c)\end{align*}
が成り立つことを,結合法則(associative law)が成り立つという.
[交換法則]集合$A$に演算$\star$が定まっているとする.このとき,任意の$a,b\in A$に対して,
\begin{align*}a\star b=b\star a\end{align*}
が成り立つことを,交換法則(commutative law)が成り立つという.
[分配法則]集合$A$に2つの演算$\circ$と$\star$が定まっているとする.このとき,任意の$a,b,c\in A$に対して,
\begin{align*}a\star(b\circ c)=(a\star b)\circ (a\star c),\quad
(a\circ b)\star c=(a\star c)\circ (b\star c)\end{align*}
が成り立つことを,分配法則(distributive law)が成り立つという.
[結合法則]と[交換法則]は1つの演算に関する性質であり,[分配法則]は2つの演算に関する性質であることに注意してください.
算数以来,実数の加法+と乗法・においてこれらの3法則は当たり前に成り立ってきました.
しかし,大学以降の数学においては交換法則が成り立たないことも珍しくなく,交換法則が成り立つ演算を可換といい,交換法則が成り立たない演算を非可換といいます.
群の定義と具体例
この節では,群を定義し,群の例を挙げます.
群とは集合と演算の組$(G,\star)$
群の定義は次の通りです.
[群]集合$G$に演算$\star$が定まっているとする.次の3条件を満たすとき,集合と演算の組$(G,\star)$を群(group)という.演算が明らかな場合は,単に$G$を群ということも多い.
- ある$e\in G$が存在して,任意の$g\in G$に対して$e\star g=g\star e=g$が成り立つ.
- 任意の$g\in G$に対して,ある$h\in G$が存在して$g\star h=h\star g=e$が成り立つ.
- 演算$\star$に関して[結合法則]が成り立つ.
加えて次を満たすとき,群$(G,\star)$は可換群(commutative group)またはアーベル群(abelian group)であるという.
- 演算$\star$に関して[交換法則]が成り立つ.
(1)の$e\in G$を単位元(identity element)といい,(2)の$h\in G$を$g$の逆元(inverse element)といいます.単位元は全ての元に対して$e\star g=g\star e=g$を満たさなければなりませんが,逆元は$g\in G$ごとに決まることに注意してください.
群は「集合」と「演算」により定まるという点を意識してください.
そのため,なんらかの集合$G$が与えられて「$G$は群か?」と問われても,演算が何か分からないため群であるかどうか答えようがないので,「$G$に定義されている演算は何ですか?」と逆に問い返すことになります.
乗法と加法の使い分け
群における慣習的な乗法と加法という言葉の使い分け方について説明します.
可換群の場合にも非可換群の場合にも群に定まっている演算は「乗法」と呼ばれることが多く,「乗法」と呼ぶ場合には演算の記号は・や×で表すことが多いです.
一方,群に定まっている演算を「加法」と言った場合には,その演算は可換であることが普通です.すなわち,非可換な演算を「加法」と呼ぶことはまずありません.
他に
- 乗法・の記号は省略することも多いが,加法+の記号は省略しない
- 乗法に関する$g$の逆元は$g^{-1}$で表し,加法に関する$g$の逆元は$-g$で表す
という慣習もあります.また,乗法による計算結果を積,加法による計算結果を和といいます.
具体例1(自明な群)
1つの元のみからなる集合$X=\{x\}$を考えます.
このとき,$X$上の演算は$(x,x)\mapsto x$しかあり得ませんが,この演算を乗法・とすることにより$(X,\cdot)$は可換群となります.
この群1つの元のみからなる集合を自明な群(trivial group)といいます.
具体例2(可換群$(\Z,+)$)
整数の集合$\Z$と,通常の加法+の組$(\Z,+)$を考えます.
ここで,「通常の加法」とは小学校から扱ってきた単なる足し算のことで,
- 任意の$n\in\Z$に対して$n+0=0+n=n$が成り立つので,単位元は0です.
- 任意の$n\in\Z$に対して$n+(-n)=(-n)+n=0$が成り立つので$n$の逆元は$-n$です.
- 整数の足し算なので[結合法則]は成り立ちます.
- 整数の足し算なので[交換法則]は成り立ちます.
よって,組$(\Z,+)$が可換群であることが分かりました.
具体例3(可換群$(\Q\setminus\{0\},\cdot)$)
有理数の集合から0を除いた集合$\Q\setminus\{0\}$と,通常の乗法・の組$(\Q\setminus\{0\},\cdot)$を考えます.
ここで,「通常の乗法」とは小学校から扱ってきた単なる掛け算のことで,
- 任意の$x\in\Q\setminus\{0\}$に対して$1\cdot x=x\cdot1=x$が成り立つので,単位元は1です.
- 任意の$x\in\Q\setminus\{0\}$に対して$x\cdot\dfrac{1}{x}=\dfrac{1}{x}\cdot x=1$が成り立つので,$x$の逆元は$\dfrac{1}{x}$です.
- 有理数の掛け算なので[結合法則]は成り立ちます.
- 有理数の掛け算なので[交換法則]は成り立ちます.
よって,組$(\Q\setminus\{0\},\cdot)$が可換群であることが分かりました.
具体例4(群でない組$(\Z,\cdot)$)
整数の集合$\Z$と,通常の乗法・の組$(\Z,\cdot)$を考えます.
- 任意の$n\in\Z$に対して$1\cdot n=n\cdot1=n$が成り立つ
- $2\in\Z$に対して$2\cdot n=1$をみたすような$\Z$の元は存在しないから,$2\in\Z$は逆元を持たない
となっています.群は任意の元が逆元を持たなければなりませんから,組$(\Z,\cdot)$は群でないことが分かりました.
例2,例3,例4から,次のことが分かりますね.
- 例2と例4から,同じ集合であっても演算が異なれば群であったりなかったりする
- 例3と例4から,同じ演算であっても集合が異なれば群であったりなかったりする
具体例5(可換群$(\Z_6,+)$)
集合$\Z_6=\{\overline{0},\overline{1},\overline{2},\overline{3},\overline{4},\overline{5}\}$と,演算+を
$\overline{m}+\overline{n}=\overline{(\text{$m+n$を6で割った余り})}$
の組$(\Z_6,+)$を考えます.例えば,
\begin{align*}&\overline{1}+\overline{1}=\overline{2},\quad
\overline{3}+\overline{2}=\overline{5},
\\&\overline{4}+\overline{5}=\overline{3},\quad
\overline{2}+\overline{4}=\overline{0}\end{align*}
といった具合に,6に達すると0に戻る演算がいまの演算+ですね.
合同式を知っていれば$\operatorname{mod}\ 6$で計算していると考えれば分かりやすいでしょう.
このとき,
- 任意の$\overline{n}\in\Z_6$に対して$\overline{n}+\overline{0}=\overline{0}+\overline{n}=\overline{n}$が成り立つので,単位元は$\overline{0}$です.
- $\overline{0}+\overline{0}=\overline{0}$, $\overline{1}+\overline{5}=\overline{5}+\overline{1}=\overline{0}$, $\overline{2}+\overline{4}=\overline{4}+\overline{2}=\overline{0}$, $\overline{3}+\overline{3}=\overline{0}$なので,$-\overline{0}=\overline{0}$, $-\overline{1}=\overline{5}$, $-\overline{2}=\overline{4}$, $-\overline{3}=\overline{3}$, $-\overline{4}=\overline{2}$, $-\overline{5}=\overline{1}$となって,任意の$n\in\Z_6$に対して,$n$の逆元が存在します.
- $\Z$の通常の加法+では[結合法則]が成り立つから,$\Z$の計算をして6で割った余りを考えることで[結合法則]は成り立ちます.
- $\Z$の通常の加法+では[交換法則]が成り立つから,$\Z$の計算をして6で割った余りを考えることで[交換法則]は成り立ちます.
よって,組$(\Z_6,+)$が可換群であることが分かりました.
具体例6(可換群$(\Mat_{mn}(\R),+)$)
実数成分の$m\times n$行列全部の集合$\Mat_{mn}(\R)$と,通常の加法+の組$(\Mat_{mn}(\R),+)$は可換群です.
- 任意の$A\in\Mat_{mn}(\R)$に対して$A+O=O+A=A$が成り立つので,単位元は零行列$O$です.
- 任意の$A\in\Mat_{mn}(\R)$に対して$A+(-A)=(-A)+A=0$が成り立つので,$A$の逆元は$-A$です.
- 各成分で$\R$の加法なので[結合法則]は成り立ちます.
- 各成分で$\R$の加法なので[交換法則]は成り立ちます.
よって,組$(\Mat_{mn}(\R),+)$が可換群であることが分かりました.
具体例7(非可換群$(\mathrm{GL}_n(\R),\cdot)$)
実数成分の$n$次正則行列の集合$\mathrm{GL}_n(\R)$と,通常の乗法・の組$(\mathrm{GL}_n(\R),\cdot)$は群ですが,可換ではありません.
- 任意の$A\in\mathrm{GL}_n(\R)$に対して$AI=IA=A$が成り立つので,単位元は単位行列$I$です.
- 任意の$A\in\mathrm{GL}_n(\R)$に対して$A\cdot A^{-1}=A^{-1}\cdot A=0$が成り立つので,$A$の逆元は逆行列$A^{-1}$です.
- 行列の積なので[結合法則]は成り立ちます.
- 行列の積なので[交換法則]は成り立ちません.
よって,組$(\mathrm{GL}_n(\R),\cdot)$は群ですが,可換群ではないことが分かりました.
$(\mathrm{GL}_n(\R),\cdot)$は一般線形群(general linear group)とよばれており,重要な非可換群のひとつです.
具体例8(非可換群$(S_n,\cdot)$)
$n$次の置換全部の集合$S_n$と,置換の合成$\circ$として定まる積・の組$(S_n,\cdot)$は群ですが,可換ではありません.
- $\epsilon\in S_n$を単位置換とすると,任意の$\sigma\in S_n$に対して$\sigma\cdot\epsilon=\epsilon\cdot\sigma=\sigma$が成り立つので,単位元は単位置換$\epsilon$です.
- 任意の$\sigma\in S_n$に対して$\sigma\cdot \sigma^{-1}=\sigma^{-1}\cdot \sigma=0$が成り立つので,$\sigma$の逆元は逆置換$\sigma^{-1}$です.
- 置換の積(合成)なので[結合法則]は成り立ちます.
- 置換の積(合成)なので[交換法則]は成り立ちません.
よって,組$(S_n,\cdot)$は群ですが,可換群ではないことが分かりました.
群$(S_n,\cdot)$は$n$次対称群(symmetric group)とよばれており,重要な非可換群のひとつです.
群論の参考文献
以下は群論の参考文献です.
代数学1群論入門(雪江明彦 著/日本評論社)
本書は群論の入門書です.
具体例が多く行間が少ないため,初学者にも非常に読みやすい良著です.さらに,章末問題が豊富な上に解答の解説も非常に丁寧です.
章末問題のレベルもその章で学んだ基本的な内容から,少し考える問題まで様々なので理解を深めるのに非常に便利です.
また,「群論入門」は予備知識をあまり仮定せず,必要事項を第1章にまとめてあり,1から独学で学ぶことができる点も嬉しいところですね.
なお,本書について,詳しくは以下の書評を参照してください.

環の定義と具体例
この節では,環を定義し,環の例を挙げます.
環とは集合と2つの演算の組
環の定義は次の通りです.
[環]集合$R$に2つの演算+, ・が定まっているとする.次の4条件を満たすとき,集合と演算の組$(R,+,\cdot)$を環(ring)という.演算が明らかな場合は,単に$R$を環ということも多い.
- $(R,+)$は可換群である.
- ある$e\in R$が存在して,任意の$r\in R$に対して$e\cdot r=r\cdot e=r$が成り立つ.
- 演算・に関して[結合法則]が成り立つ.
- 演算+と・に関して[分配法則]が成り立つ.
このとき,+を加法,・を乗法という.加えて次をみたすとき,環$(R,+,\cdot)$は可換環 (commutative ring)であるという.
- 演算・に関して[交換法則]が成り立つ.
群の場合の演算は+も・も用いることがありますが,環の場合にはほぼ加法に+を,乗法に・を用います.
条件1の加法+に関する単位元を加法単位元(additive identity)と零元(zero element)といい0で表し,条件2の$e\in R$を乗法単位元(multiplicative identity)といい1で表します.
- 条件1は加法+に関する条件
- 条件2と条件3は乗法・に関する条件
- 条件4は加法と乗法に関する条件
ですね.
加法+と乗法・は別々に勝手にとっていいわけではなく,条件4の[分配法則]が成り立つ程度に加法+と乗法・の整合性を保っていなければならないというわけですね.
また,環においては,乗法・に関して逆元を持たない元があっても構いません.
群においてもそうでしたが,「有理数の集合$\Q$は環か?」などと問われても演算が何であるか分からないため環であるかどうか答えようがなく,「$\Q$に定義されている加法と乗法は何ですか?」と逆に問い返すことになります.
具体例1(零環)
1つの元のみからなる集合$X=\{x\}$を考えます.
このとき,$X$上の演算は$(x,x)\mapsto x$しかあり得ませんが,この演算を加法+と乗法・とすることにより$(X,+,\cdot)$は可換環となります.
この群1つの元のみからなる集合を零環(zero ring)といいます.
環に関する多くの理論は加法単位元0と乗法単位元1が異なるとして考える方が都合が良く,これらが一致する零環には一般論が通用せず都合が悪いことが多いです.
そのため,環を考える際には初めから$0\neq1$として零環を除いておくことが多いです.
具体例2(可換環$(\Q,+,\cdot)$)
有理数の集合$\Q$と,通常の加法+と乗法・の組$(\Q,+,\cdot)$は可換環です.
- 加法+に関して$\Q$は可換群です:
- 任意の$x\in\Q$に対して$x+0=0+x=x$が成り立つので,加法単位元は0です.
- 任意の$x\in\Q$に対して$x+(-1)x=(-1)x+x=0$が成り立つので,$x$の逆元は$(-1)x$です.
- 有理数の足し算なので,[結合法則]は成り立ちます.
- 有理数の足し算なので,[交換法則]は成り立ちます.
- 任意の$r\in\Q$に対して$1\cdot r=r\cdot 1=r$が成り立つので,乗法単位元は1です.
- 有理数の掛け算なので[結合法則]が成り立ちます.
- 有理数の足し算と掛け算なので[分配法則]は成り立ちます.
- 有理数の掛け算なので[交換法則]は成り立ちます.
したがって,組$(\Q,+,\cdot)$が可換環であることが分かりました.
具体例3(可換環$(\R[x],+,\cdot)$)
実数係数多項式の集合$\R[x]$と,通常の加法+と乗法・の組$(\R[x],+,\cdot)$は可換環です.
- 加法+に関して$\R[x]$は可換群です:
- 任意の$f(x)\in\R[x]$に対して$f(x)+0=0+f(x)=f(x)$が成り立つので,加法単位元は0(恒等的に値0の多項式)です.
- 任意の$f(x)\in\R[x]$に対して$f(x)+(-1)f(x)=(-1)f(x)+f(x)=0$が成り立つので,$-f(x)=(-1)f(x)$です.
- 有理数の足し算なので[結合法則]は成り立ちます.
- 有理数の足し算なので[交換法則]は成り立ちます.
- 任意の$f(x)\in\R[x]$に対して$1\cdot f(x)=f(x)\cdot 1=r$が成り立つので,乗法単位元は1(恒等的に値1の多項式)です.
- 多項式の掛け算なので[結合法則]が成り立ちます.
- 多項式の足し算と掛け算なので[分配法則]は成り立ちます.
- 多項式の掛け算なので[交換法則]は成り立ちます.
したがって,組$(\R[x],+,\cdot)$が可換環であることが分かりました.
具体例4(可換環$(\Z_6,+,\cdot)$)
群の具体例でも考えた集合$\Z_6=\{\overline{0},\overline{1},\overline{2},\overline{3},\overline{4},\overline{5}\}$において,加法+と乗法・を
- 加法+:$\overline{m}+\overline{n}=\overline{(\text{$m+n$を6で割った余り})}$
- 乗法・:$\overline{m}\cdot\overline{n}=\overline{(\text{$mn$を6で割った余り})}$
と定めると,組$(\Z_6,+,\cdot)$は可換環です.
加法についても乗法についても,6に達すれば0に戻るような演算になっていますね.
- 加法+に関して$\Z_6$は可換群です(群の具体例で確認済).
- 任意の$n\in\Z_6$に対して$1\cdot n=n\cdot 1=n$が成り立つので,乗法単位元は1です.
- $\Z$の通常の乗法・では[結合法則]が成り立つので,$\Z$の計算をして6で割った余りを考えることで[結合法則]は成り立ちます.
- $\Z$の通常の加法+と乗法・では[分配法則]が成り立つので,$\Z$の計算をして6で割った余りを考えることで[分配法則]は成り立ちます.
- $\Z$の通常の乗法・では[交換法則]が成り立つので,$\Z$の計算をして6で割った余りを考えることで[交換法則]は成り立ちます.
したがって,組$(\Z_6,+,\cdot)$が可換環であることが分かりました.
具体例5(非可換環$(\Mat_(\R),+,\cdot)$)
実数成分の$n$次正方行列の集合$\Mat_n(\R)$と,通常の加法+と乗法・の組$(\Mat_n(\R),+,\cdot)$は環ですが,可換環ではありません.
- 加法+に関して$\Mat_n(\R)$は可換群です:
- 加法単位元は零行列$O$です.
- 任意の$A\in \Mat_n(\R)$に対して,$(-1)A$が$A$の逆元です.
- 通常の行列の加法+なので[結合法則]は成り立ちます.
- 通常の行列の加法+なので[交換法則]は成り立ちます.
- 乗法単位元は単位行列$I$です.
- 通常の行列の乗法・なので[結合法則]は成り立ちます.
- 通常の行列の加法+と乗法・なので[分配法則]は成り立ちます.
- 通常の行列の乗法・なので[交換法則]は成り立ちません.
したがって,組$(\Mat_n(\R),+,\cdot)$が環ですが,可換環ではないことが分かりました.
体の定義と具体例
この節では,体を定義し,体の例を挙げます.
体とは0以外が乗法逆元ももつ可換環
体の定義は次の通りです.
[体]零環でない可換環$(F,+,\cdot)$が体(field)であるとは,任意の$a\in F\setminus\{0\}$に対して乗法逆元$a^{-1}$が存在することをいう.
可換環においては,乗法・に関する逆元は条件に含まれていませんでした.そこで「可換環の全ての元に逆元が存在する」という条件を付け加えたものが体というわけです.
大雑把に言えば,体は可換な加乗除ができる集合ということですね.なお,
- 加法単位元0以外の全ての元に逆元を持つ環を可除環(division ring)
- 非可換な可除環を斜体(skew field)
といいます.ただし,「可除環」と「斜体」の定義を同じとする流儀もあるので注意が必要です.
具体例1(体$(\Q,+,\cdot)$)
有理数の集合$\Q$と,通常の加法+と乗法・の組$(\Q,+,\cdot)$は体です.
環の例1で可換環であることは確かめました.
また,乗法単位元は1であり,任意の$x\in\Q\setminus\{0\}$に対して,$x$の乗法・に関する逆元$\dfrac{1}{x}\in\Q$が存在します.
したがって,組$(\Q,+,\cdot)$が体であることが分かりました.
同様にして,実数全部の集合$\R$,複素数全部の集合$\C$も通常の加法+と乗法・により体となります.
具体例2(体$(\Z/_7,+,\cdot)$)
$\mathbb{F}_7=\Z_7=\{0,1,2,3,4,5,6\}$において,加法+と乗法・を
- 加法+:$a,b\in\mathbb{F}_7$に対して,$\Z$の通常の加法で$a+b$を計算して,7で割った余りを$\mathbb{F}_7$の和とする.
- 乗法・:$a,b\in\mathbb{F}_7$に対して,$\Z$の通常の乗法で$a\cdot b$を計算して,7で割った余りを$\mathbb{F}_7$の積とする.
と定めると,組$(\mathbb{F}_7,+,\cdot)$は体です.
環の例4の$(\Z_6,+,\cdot)$と同様にイメージとしては$0,1,2,3,4,5,6,0,1,2,\dots$のように7になると0に戻る演算だと思えばよく,環の例3と同様に考えて$\mathbb{F}_7$が可換環であることが分かります.
また,乗法単位元は1であり,
\begin{align*}1\cdot1=1,\quad
2\cdot4=1,\quad
3\cdot5=1,\quad
6\cdot6=1\end{align*}
なので,任意の$n\in\mathbb{F}_7\setminus\{0\}$に対して,$n$の乗法・に関する逆元が存在します.
よって,組$(\mathbb{F}_7,+,\cdot)$が体であることが分かりました.
実は,一般に2以上の整数$p$に対して
- $p$は素数である
- $(\Z/p\Z,+,\cdot)$は体である
が同値であり,素数$p$に対して$(\Z/p\Z,+,\cdot)$は体となり,$\Z/p\Z$を$\mathbb{F}_p$で表すことが多いです.
環の例4の$(\Z_6,+,\cdot)$は体ではありません.これは逆元をもたない元が存在するためです.
例えば,$2\in\Z_6$にはどの$0,1,\dots,5\in\Z_6$をかけても1となりません.つまり,2の逆元は存在しません.
具体例3(体$(\Q[\sqrt{5}],+,\cdot)$)
集合$\Q[\sqrt{5}]=\set{a+b\sqrt{5}}{a,b\in\Q}$と,通常の加法+と乗法・の組$(\Q[\sqrt{5}],+,\cdot)$は可換環です.
加法+と乗法・が演算になっていることを確認しなければなりませんが,それは任意の$a+b\sqrt{5},c+d\sqrt{5}\in\Q[\sqrt{5}]$に対して,
\begin{align*}&(a+b\sqrt{5})+(c+d\sqrt{5})=(a+b)+(c+d)\sqrt{5}\in\Q[\sqrt{5}],
\\&(a+b\sqrt{5})\cdot(c+d\sqrt{5})=(ac+5bd)+(ad+bc)\sqrt{5}\in\Q[\sqrt{5}]\end{align*}
なので,確かに加法+と乗法・は$\Q[\sqrt{5}]$上の演算ですね.
- 加法+に関して$\Q[\sqrt{5}]$は可換群です:
- 任意の$x\in\Q[\sqrt{5}]$に対して$x+0=0+x=x$が成り立つので,加法単位元は0です.
- 任意の$x\in\Q[\sqrt{5}]$に対して$x+(-x)=(-x)+x=0$が成り立つので,$-x$が$x$の逆元です.
- 実数の足し算なので[結合法則]は成り立ちます.
- 実数の足し算なので[交換法則]は成り立ちます.
- 任意の$x\in\Q[\sqrt{5}]$に対して$1\cdot x=x\cdot 1=x$が成り立つので,乗法単位元は1です.
- 実数の掛け算なので[結合法則]が成り立ちます.
- 実数の足し算と掛け算なので[分配法則]は成り立ちます.
- 有理数の掛け算なので[交換法則]は成り立ちます.
- $\Q[\sqrt{5}]$の$0$でない任意の元$a+b\sqrt{5}$に対して,$\dfrac{a-b\sqrt{5}}{a^2-5b^2}\in\Q[\sqrt{5}]$が逆元として存在します.
したがって,組$(\Q[\sqrt{5}],+,\cdot)$が体であることが分かりました.
環論・体論の参考文献
以下は,環論と体論の参考文献です.
代数学2 環と体とガロア理論 (雪江明彦著,日本評論社)
本書は環論,体論の入門書です.
先ほど紹介した第1巻の「群論入門」と同じく,具体例と章末問題が豊富で,独学でも十分に読み進めることができます.
特に代数学の1つの大きな分野であるガロア理論について具体例を丁寧に扱っているのは初学者にありがたいですね.
なお,私の体験としてガロア理論で様々な例を扱うのは良い演習になるようで,本書のガロア理論の具体例をしっかり読み込むことで環論と体論の理解がより深まりました.
ただし,残念なのは誤植が散見されることで,読み進める際にはきちんと自身で行間を埋めつつ読むようにしてください.

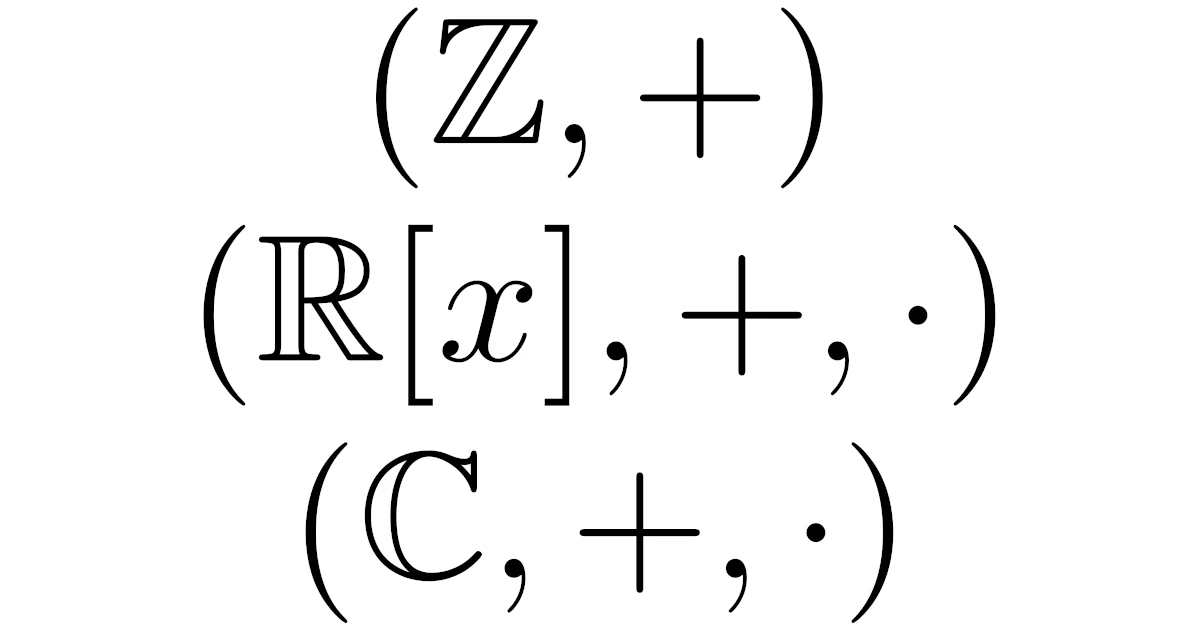


コメント
独学で代数学を勉強しております。専門書に載っている$(\Q,+,\cdot)$のような表記の意味などが良くわからずとても苦戦しておりましたが、この記事のお陰で理解が深まりました。ありがとうございます!!
コメントをありがとうございます.
お力になれたようで嬉しく思います!
とてもよくわかりました
一部難しいところもありましたが・・・またいずれ見に来ます
それにしても、高校を卒業してすぐこんな勉強をするなんて、大学生ってすごいんですねえ
コメントをありがとうございます!
高校を卒業してすぐというわけではありませんが,大学に入ると高校のときよりも抽象度の高い数学を学ぶことになりますね.
抽象度を高めるとそれだけ応用の幅が広くなるので,たとえば群は純粋数学だけではなく,化学の分子構造の対称性などに応用されたりします.
ぜひまた勉強してみてください!