領域$D$上の正則関数$f$はコーシーの積分公式を用いることでテイラー展開できるのでした.
1点$\alpha$で複素微分可能か不明であっても,$\alpha$を除いた$\alpha$の近くで正則なら
\begin{align*}f(z)=\dots+\frac{c_{-2}}{(z-\alpha)^2}+\frac{c_{-1}}{z-\alpha}+c_0+c_1(z-\alpha)+c_2(z-\alpha)^2+\dots.\end{align*}
と負冪の項$c_{-k}(z-\alpha)^{-k}$も用いて$f$を級数で表すことは可能で,この展開を$f$の$\alpha$中心のローラン展開といいます.
ローラン展開の$-1$次の係数$c_{-1}$は$f$の$\alpha$での留数といい,この一連の記事の目標である留数定理に重要な役割を果たします.
この記事では
- ローラン展開と留数
- ローラン展開可能性の証明
- ローラン展開の一意性
を順に説明します.
「複素解析の基本」の一連の記事
ローラン展開と留数
まずは複素関数のテイラー展開について確認し,そのあとにテイラー展開と比較してローラン展開を説明します.
テイラー展開の復習
[テイラー展開可能性]領域$D$上の正則関数$f$と$\alpha\in D$を考える.$\alpha$中心の円周$C$の周および内部が$D$に含まれるとき,
\begin{align*}f(z)=c_0+c_1(z-\alpha)+c_2(z-\alpha)^2+\dots&
\\(c_0,c_1,c_2,\dots\in\C)&\end{align*}
と$\alpha$中心でテイラー展開可能である.ただし,$z$は円周$C$の内部の点である.
複素関数$f$が領域$D$上の全ての点で1回でも複素微分可能なら$f$を正則関数と呼ぶのでしたから,この定理から「領域$D$上の任意の点で1回複素微分可能な複素関数は,$D$上の任意の点を中心としてテイラー展開可能」と言い換えることもできますね.
ローラン展開の定義とローラン展開可能性
テイラー展開は$(z-\alpha)$の正冪の級数で表すことを言いましたが,負冪まで許した級数をローラン(Laurent)展開といいます.
$\alpha\in\C$に対して,複素平面上の領域$\alpha$を除くある開近傍上で複素関数$f$が
\begin{align*}f(z)=&\dots+\frac{c_{-2}}{(z-\alpha)^{2}}+\frac{c_{-1}}{z-\alpha}+c_{0}+c_{1}(z-\alpha)+c_{2}(z-\alpha)^{2}+\dots
\\\Bigl(=&\sum_{n=-\infty}^{\infty}c_n(z-\alpha)^n\Bigr)\end{align*}
と表せるとき,この右辺を$f$の$\alpha$中心のローラン展開という.また,$f$が$\alpha$中心のローラン展開で表せるとき,$f$は$\alpha$でローラン展開可能であるという.
領域$D$上の1点$\alpha$での複素関数$f$の微分可能性が分からない場合,テイラー展開ができるかは不明ですが,$\alpha$の近くで複素微分可能なら$f$は$\alpha$中心でローラン展開可能であることが証明できます.
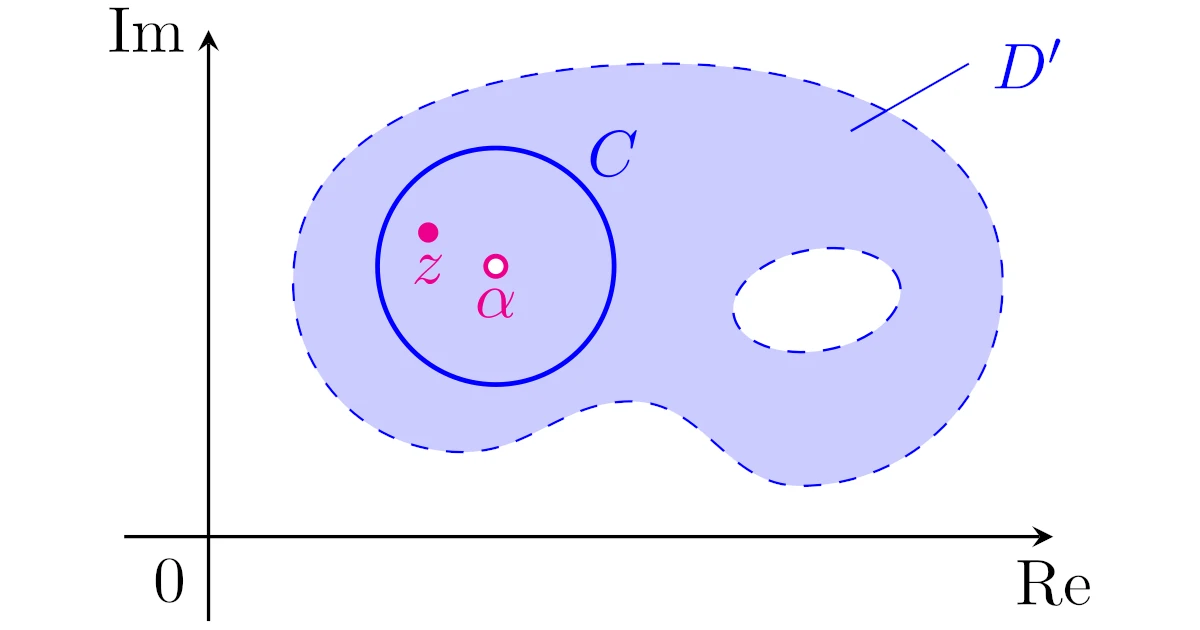
[ローラン展開可能性]領域$D$から$\alpha\in D$を除いた領域$D’$上の正則関数$f$を考える.$\alpha$中心の円周$C$の周および内部が$D$に含まれるとき,$f$は$C$の内部から$\alpha$を除いた領域で
\begin{align*}f(z)=&\dots+\frac{c_{-2}}{(z-\alpha)^{2}}+\frac{c_{-1}}{z-\alpha}
\\&\quad+c_{0}+c_{1}(z-\alpha)+c_{2}(z-\alpha)^{2}+\dots\end{align*}
と$\alpha$中心でローラン展開可能である.ただし,$z$は円周$C$の$\alpha$を除く内部の点である.
先ほど説明した[テイラー展開可能性]との違いは,点$\alpha$で微分可能かが分かっているかどうかだけで
- $\alpha$を含む$\alpha$の近くで複素微分可能 → $\alpha$でテイラー展開可能
- $\alpha$を除く$\alpha$の近くで複素微分可能 → $\alpha$でローラン展開可能
というわけですね.
上の$\alpha$でのローラン展開で$\alpha$で微分可能であることが分かれば$c_{-1}=c_{-2}=c_{-3}=\dots=0$となってテイラー展開可能であることになりますね.
留数の定義
上の[ローラン展開]の$k$次の係数$c_{k}$はのちに説明するように
\begin{align*}c_{k}=\frac{1}{2\pi i}\int_{C}\frac{f(\zeta)}{(\zeta-\alpha)^{k+1}}\,d\zeta\end{align*}
となります.とくに$k=-1$のときは
\begin{align*}c_{-1}=\frac{1}{2\pi i}\int_{C}f(\zeta)\,d\zeta
\iff \int_{C}f(\zeta)\,d\zeta=2\pi i c_{-1}\end{align*}
となります.つまり,留数$\mrm{Res}(f,\alpha)$を求めて$2\pi i$倍すれば$\alpha$周りでの$f$の複素積分が求まるわけですね.
このように,この$-1$次の係数$c_{-1}$は複素積分に密接に関わるものとして以下のように定義されます.
上のローラン展開の$c_{-1}$を$f$の$\alpha$における留数(residue)といい,$\mrm{Res}(f,\alpha)$や$\mrm{Res}_{\alpha}f$などと表す.
“residue”は「残り物」という意味です.ローラン展開$f(z)=\dsum_{n=-\infty}^{\infty}c_n(z-\alpha)^n$に対して,
\begin{align*}\int_{C}f(z)\,dz=2\pi ic_{-1}\end{align*}
なので,$c_{-1}$は積分しても消えずに「留まる数」ということで留数と名付けられているわけですね.
この記事の最後で説明するようにローラン展開は1通りしかないため,留数は1つに定まります.
ローラン展開可能性の証明
それでは[ローラン展開可能性]の定理を証明しましょう.
正則関数のテイラー展開もそうでしたが,ローラン展開も次のコーシーの積分公式を用いて導かれます.
[ローラン展開可能性(再掲)]領域$D$から$\alpha\in D$を除いた領域$D’$上の正則関数$f$を考える.$\alpha$中心の円周$C$の周および内部が$D$に含まれるとき,$f$は$C$の内部から$\alpha$を除いた領域で
\begin{align*}f(z)=&\dots+\frac{c_{-2}}{(z-\alpha)^{2}}+\frac{c_{-1}}{z-\alpha}
\\&\quad+c_{0}+c_{1}(z-\alpha)+c_{2}(z-\alpha)^{2}+\dots\end{align*}
と$\alpha$中心でローラン展開可能である.ただし,$z$は円周$C$の$\alpha$を除く内部の点である.
$C$の$\alpha$を除く内部の点$z$を任意にとる.また,$C_{z}$, $C’$はそれぞれ$C$の内部の$z$, $\alpha$中心の円周で,互いに外部にあるようにとる.
ただし,$C$, $C_z$, $C’$はいずれも正の向きがついているとする.
ステップ1($f$を2つの項に分ける)
このとき,$D$上で$f$は点$\alpha$のみで微分不可能であり,$\frac{1}{\zeta-z}$は点$z$のみで微分不可能であることに注意すると,コーシーの積分定理より
\begin{align*}\int_{C}\frac{f(\zeta)}{\zeta-z}\,d\zeta=\int_{C_{z}}\frac{f(\zeta)}{\zeta-z}\,d\zeta+\int_{C’}\frac{f(\zeta)}{\zeta-z}\,d\zeta\end{align*}
が成り立つ.また,コーシーの積分公式より
\begin{align*}f(z)=\frac{1}{2\pi i}\int_{C_{z}}\frac{f(\zeta)}{\zeta-z}\,d\zeta\quad\dots(**)\end{align*}
が成り立つので,これらを併せて
\begin{align*}f(z)&=\frac{1}{2\pi i}\int_{C}\frac{f(\zeta)}{\zeta-z}\,d\zeta-\frac{1}{2\pi i}\int_{C’}\frac{f(\zeta)}{\zeta-z}\,d\zeta
\\&=:I+I\!I\end{align*}
が成り立つ.$I$は[テイラー展開可能性]の証明と同様に
\begin{align*}&I=a_{0}+a_{1}(z-\alpha)+a_{2}(z-\alpha)^{2}+\dots,
\\&c_{k}=\frac{1}{2\pi i}\int_{C}\frac{f(\zeta)}{(\zeta-\alpha)^{k+1}}\,d\zeta\quad(k=1,2,\dots)\end{align*}
とテイラー展開できるから,あとは$I\!I$を
\begin{align*}I\!I=\frac{c_{-1}}{z-\alpha}+\frac{c_{-2}}{(z-\alpha)^{2}}+\dots\end{align*}
と展開できることを示せば良い.
ステップ2($I\!I$の変形)
$I\!I$の積分の中身は
\begin{align*}\frac{f(\zeta)}{\zeta-z}
&=\frac{f(\zeta)}{z-\alpha}\cdot\frac{1}{\frac{\zeta-z}{z-\alpha}}
\\&=-\frac{f(\zeta)}{z-\alpha}\cdot\frac{1}{1-\frac{\zeta-\alpha}{z-\alpha}}
\\&=-\frac{f(\zeta)}{z-\alpha}\sum_{k=1}^{\infty}\bra{\frac{\zeta-\alpha}{z-\alpha}}^{k-1}\end{align*}
ただし,$|\zeta-\alpha|<|z-\alpha|$より$|\frac{\zeta-\alpha}{z-\alpha}|<1$だから,$\frac{1}{1-\frac{\zeta-\alpha}{z-\alpha}}$は初項1,公比$\frac{\zeta-\alpha}{z-\alpha}$の等比級数であることを用いた.よって,
\begin{align*}I\!I=-\frac{1}{2\pi i}\int_{C’}\frac{f(\zeta)}{z-\alpha}\sum_{k=1}^{\infty}\bra{\frac{\zeta-\alpha}{z-\alpha}}^{k-1}\,d\zeta\quad\dots(*)\end{align*}
が成り立つ.
ステップ3(級数と積分の順序交換)
$(*)$の極限(級数)と積分の順序交換をするため,$\int_{C}$の中の$C$上の複素関数を
\begin{align*}g_n(\zeta):=\sum_{k=1}^{n}\frac{f(\zeta)}{z-\alpha}\bra{\frac{\zeta-\alpha}{z-\alpha}}^{k-1}\end{align*}
と定め,関数列$\{g_n\}_{n=0}^{\infty}$が$n\to\infty$で$C’$上一様収束することを示す.
$C’$の半径を$R$とする.円周$C’$は有界閉集合(コンパクト集合)なので,$C’$上で連続な$f$は最大値$M$をもつから,任意の$\zeta\in C’$に対して
\begin{align*}\abs{\frac{f(\zeta)}{z-\alpha}\bra{\frac{\zeta-\alpha}{z-\alpha}}^{k-1}}
\le\frac{M}{|z-\alpha|}\bra{\frac{R}{|z-\alpha|}}^{k-1}\end{align*}
が成り立つ.$\frac{R}{|z-\alpha|}<1$だから級数$\sum\limits_{k=0}^{\infty}\frac{M}{|z-\alpha|}\bra{\frac{R}{|z-\alpha|}}^{k-1}$は収束するので,ワイエルシュトラスのM判定法より関数列$\{g_n\}$は一様収束する.
よって,$(*)$で極限(級数)と積分の順序交換ができて
\begin{align*}I\!I&=-\frac{1}{2\pi i}\sum_{k=1}^{\infty}\frac{1}{(z-\alpha)^k}\int_{C’}f(\zeta)(\zeta-\alpha)^{k-1}\,d\zeta
\\&=\frac{c_{-1}}{z-\alpha}+\frac{c_{-2}}{(z-\alpha)^{2}}+\frac{c_{-3}}{(z-\alpha)^{3}}+\dots\end{align*}
を得る.ただし,$c_{-k}=\dfrac{1}{2\pi i}\dint_{C’}f(\zeta)(\zeta-\alpha)^{k-1}\,d\zeta$($k=1,2,\dots$)とおいた.
この係数$c_k$は$z$によらないから示された.
なお,最後の$c_{-k}=\dfrac{1}{2\pi i}\dint_{C’}f(\zeta)(\zeta-\alpha)^{k-1}\,d\zeta$は$-k$を$k$に換え,また積分経路$C’$を$C$に変形すれば
\begin{align*}c_{k}=\frac{1}{2\pi i}\int_{C}\frac{f(\zeta)}{(\zeta-\alpha)^{k+1}}\,d\zeta\end{align*}
となり,$I$の$k\ge0$のときと$I\!I$の$k<0$のときで係数$c_k$は同じ形であることが分かりますね.
ローラン展開の一意性
上の[ローラン展開可能性]の証明はコーシーの積分公式からローラン展開の形に変形できることを証明しただけで,もしかすると別の方法をとれば別の係数$c_k$のローラン展開にできる可能性が残っています.
しかし,実際にはそんなことはなくローラン展開の係数$c_k$は一意に決まります.
[ローラン展開の一意性]上のローラン展開は一意である.すなわち,
\begin{align*}f(z)=\sum_{n=-\infty}^{\infty}c_n(z-\alpha)^n=\sum_{n=-\infty}^{\infty}d_n(z-\alpha)^n\end{align*}
と2通りにローラン展開できたとすると,$c_n=d_n$($n\in\Z$)が成り立つ.
任意に円周$C$の半径を$R$とし,任意に$k\in\Z$をとる.また,任意に$r\in(0,R)$をとる.
$C$上の点で整級数
\begin{align*}\sum_{n=0}^{\infty}c_n(z-\alpha)^{n-k-1},\quad
\sum_{n=0}^{\infty}d_n(z-\alpha)^{n-k-1}\end{align*}
が収束するから,微分積分学の整級数と同様に中心$\alpha$,半径$r$の円内部$A_2=\set{z\in\C}{|z-\alpha|<r}$でいずれの整級数も一様収束する.
同様に,
\begin{align*}\sum_{n=-\infty}^{-1}c_n(z-\alpha)^{n-k-1},\quad
\sum_{n=-\infty}^{-1}d_n(z-\alpha)^{n-k-1}\end{align*}
は中心$\alpha$,半径$r$の円外部$A_2=\set{z\in\C}{r<|z-\alpha|}$で一様収束する.
$r\in(0,R)$は任意だったから,領域$A_1\cap A_2=\set{z\in\C}{0<|z-\alpha|<R}$で
\begin{align*}\sum_{n=-\infty}^{\infty}c_n(z-\alpha)^{n-k-1},\quad
\sum_{n=-\infty}^{\infty}d_n(z-\alpha)^{n-k-1}\end{align*}
はいずれも一様収束する.
よって,$\dsum_{n=-\infty}^{\infty}c_n(z-\alpha)^n=\dsum_{n=-\infty}^{\infty}d_n(z-\alpha)^n$の両辺に$(z-\alpha)^{-k-1}$をかけて,両辺を$C’$上で積分すると
\begin{align*}&\int_{C_r}\sum_{n=-\infty}^{\infty}c_n(z-\alpha)^{n-k-1}\,dz=\int_{C_r}\sum_{n=-\infty}^{\infty}d_n(z-\alpha)^{n-k-1}\,dz
\\&\iff\sum_{n=-\infty}^{\infty}\int_{C_r}c_n(z-\alpha)^{n-k-1}\,dz=\sum_{n=-\infty}^{\infty}\int_{C_r}d_n(z-\alpha)^{n-k-1}\,dz\end{align*}
が成り立つ.ただし,$C_r$は中心$\alpha$,半径$r$の円周である.単純な複素積分の計算により
\begin{align*}\int_{C_r}c_n(z-\alpha)^{n-k-1}\,dz=\begin{cases}0&(n\neq k)\\2\pi i&(n\neq k)\end{cases}\end{align*}
だから,$2\pi ic_{k}=2\pi id_{k}\iff c_{k}=d_{k}$となってローラン展開の一意性が成り立つ.
また,ローラン展開が一意であることから
- テイラー展開も一意
- 留数も一意
であることが分かりますね.


コメント