次の積分を考えましょう．
次の広義積分を計算せよ．
\begin{align*}\int_{-\infty}^{\infty}\frac{1}{(x^{2}+1)^{6}}\,dx.\end{align*}
真面目に不定積分$\dint\frac{1}{(x^{2}+1)^{6}}\,dx$からこの広義積分を求めるのは大変です．
そこでこの広義積分を上手く求める方法があれば嬉しいわけですが，その方法として留数定理を用いる方法があります．
この記事では
- ローラン展開と留数定理
- 留数定理の具体例
- 留数定理の証明
を順に解説します．
「複素解析の基本」の一連の記事
留数定理
留数定理を述べるためにローラン展開を確認しておきましょう．
ローラン展開と留数
複素関数$f$の$\alpha\in\C$でのローラン展開とは，$f$を
\begin{align*}f(z)&=\dots+\frac{c_{-2}}{(z-\alpha)^{2}}+\frac{c_{-1}}{z-\alpha}
\\&\quad+c_{0}+c_{1}(z-\alpha)+c_{2}(z-\alpha)^{2}+\dots\end{align*}
と級数で表すことをいうのでした．
複素関数$f$が$\alpha$の近くで正則なら，$f$は$\alpha$でローラン展開可能だったことを思い出しておきましょう．
［ローラン展開可能性］領域$D$から$\alpha\in D$を除いた領域$D’$上の正則関数$f$を考える．$\alpha$中心の円周$C$の周および内部が$D$に含まれるとき，$f$は$C$の内部から$\alpha$を除いた領域でローラン展開可能である．
ただし，$z$は円周$C$の$\alpha$を除く内部の点であり，$(z-\alpha)^k$の係数$c_{k}$は
\begin{align*}c_{k}=\frac{1}{2\pi i}\int_{C}\frac{f(z)}{(z-\alpha)^{k+1}}\,dz\end{align*}
と一意に表される（$k=0,\pm1,\pm2,\dots$）．
係数$c_{k}$について，$k=-1$のときに注目すると
\begin{align*}\int_{C}f(z)\,dz=2\pi ic_{-1}\end{align*}
が成り立つので，$c_{-1}$は複素積分に密接に関わるものとして留数と呼ばれるのでした．
複素関数$f$の$\alpha$でのローラン展開の$(-1)$次の係数を，$f$の$\alpha$における留数（residue）といい$\mrm{Res}(f,\alpha)$や$\mrm{Res}_{\alpha}f$などと表す．
もし$f$が$\alpha$でも複素微分可能なら$f$は$\alpha$でテイラー展開可能なので，$\alpha$でのローラン展開では負冪の項がなく$c_{-1}=0$となります．よって，このとき$\mrm{Res}(f,\alpha)=0$となりますね．
留数定理
留数定理とは「複素積分がいくつかの留数の和の$2\pi i$倍で求まる」という定理で，詳しく述べると次のようになります．
［留数定理］領域$D$内に有限個の点$\alpha_{1},\dots,\alpha_{n}$があり，$D$内の閉曲線$C$がこれらの点を内部に含むとする．このとき，領域$D\setminus\{\alpha_{1},\dots,\alpha_{n}\}$上の正則関数$f$に対して
\begin{align*}\int_{C}f(z)\,dz=2\pi i\mrm{Res}(f,\alpha_{1})+\dots+2\pi i\mrm{Res}(f,\alpha_{n})\end{align*}
が成り立つ．ただし，$C$の向きは正方向とする．
もし$f$が全ての点$\alpha_{1},\dots,\alpha_{n}$が複素微分可能なら
\begin{align*}\mrm{Res}(f,\alpha_{1})=\dots=\mrm{Res}(f,\alpha_{n})=0\end{align*}
なので，$\dint_{C}f(z)\,dz=0$が成り立ちますが，これはコーシーの積分定理に他なりませんね．
つまり，複素関数が閉積分経路内に正則でない点をもつ場合にコーシーの積分定理を拡張したのが留数定理になっているわけですね．
留数定理の証明はこの記事の最後に遺し，先に留数定理の応用例を見ておきましょう．
留数定理の広義積分への応用
冒頭の問題を龍数定理を用いて解きましょう．
次の広義積分を計算せよ．
\begin{align*}\int_{-\infty}^{\infty}\frac{1}{(x^{2}+1)^{6}}\,dx.\end{align*}
いきなり解答を書いても流れが分かりにくいと思うので，まずは解答の方針を説明します．
解答の方針
最初に，問題の広義積分は
\begin{align*}\int_{-\infty}^{\infty}\frac{1}{(x^{2}+1)^{6}}\,dx=\lim_{R\to\infty}\int_{-R}^{R}\frac{1}{(x^{2}+1)^{6}}\,dx\end{align*}
であることを思い出しておきましょう．
方針１（実軸上の線分$L_R$上の複素積分に書き直す）
極限$R\to\infty$をとる前の定積分$\dint_{-R}^{R}\frac{1}{(x^{2}+1)^{6}}\,dx$は
- 実軸上の閉区間$[-R,R]$
- $f(z)=\dfrac{1}{(z^{2}+1)^{6}}$で定まる複素関数$f$
を用いれば，
\begin{align*}\int_{-R}^{R}\frac{1}{(x^{2}+1)^{6}}\,dx=\int_{L_R}f(z)\,dx\end{align*}
と複素積分で表せますね．ただし，$L_R$の向きは実軸上の負から正に向かう方向としています．
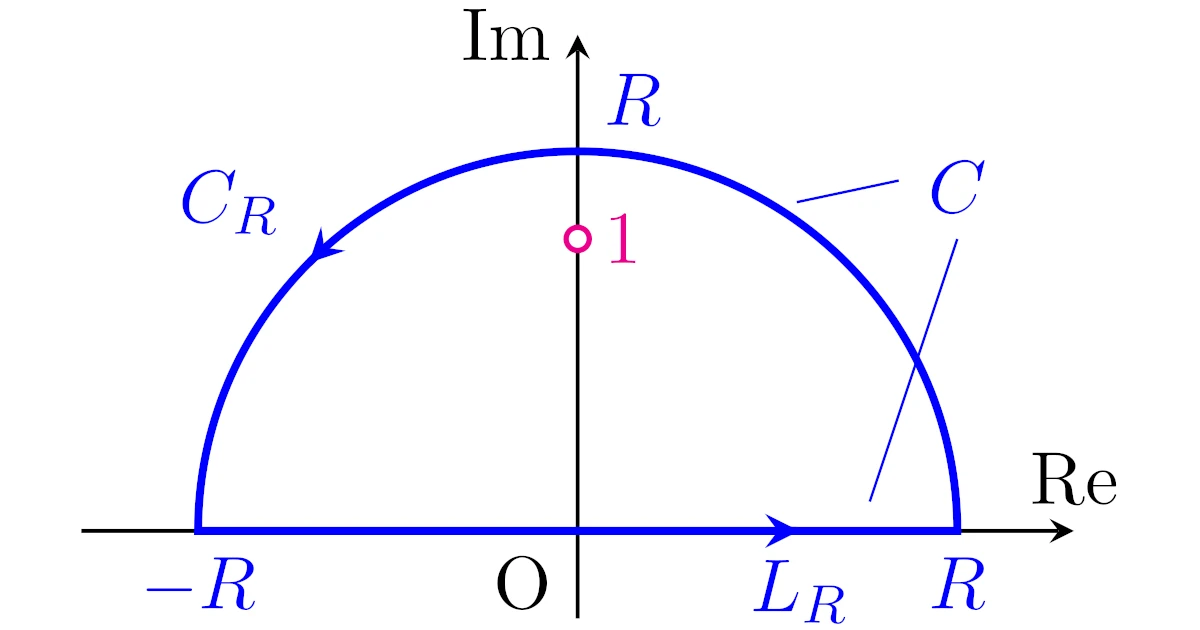
方針２（$L_R$を含む閉曲線$C$をつくる）
原点中心の上半円$C_{R}$を考え，$C_R$と$L_R$を併せた閉曲線を$C$とします．ただし，$C_R$の向きは$L_R$に自然に繋がる方向とします．
このとき，$z\in C_R$の絶対値は$R$なので，$R$が十分大きければ$C_R$上で
\begin{align*}|f(z)|=\abs{\frac{1}{(z^{2}+1)^{6}}}\approx\frac{1}{(R^2+1)^6}\end{align*}
と考えられます．いま$C_R$の長さは$\pi R$だから，
\begin{align*}\abs{\int_{C_R} f(z)\,dz}\approx\frac{\pi R}{(R^2+1)^6}\end{align*}
なので，極限$R\to\infty$をとれば０に近付くことがみてとれますね．
方針３（留数定理と極限$R\to\infty$を考える）
$R>1$なら閉曲線$C$は$f$が正則な領域に含まれ，閉曲線$C$の内部では$i$のみで$f$が複素微分不可能なので，留数定理より
\begin{align*}\int_{C}f(z)\,dz=2\pi i\operatorname{Res}{(f,i)}\end{align*}
が$R>1$によらず成り立ちます．また
\begin{align*}\int_{C}f(z)\,dz=\int_{C_R}f(z)\,dz+\int_{L_R}f(z)\,dz\end{align*}
なので両辺で極限$R\to\infty$をとれば，方針１と方針２を併せて
\begin{align*}2\pi i\operatorname{Res}{(f,i)}=0+\int_{-\infty}^{\infty}\frac{1}{(x^{2}+1)^{6}}\,dx\end{align*}
となって，問題の広義積分が得られることになります．
解答例
（再掲）次の広義積分を計算せよ．
\begin{align*}\int_{-\infty}^{\infty}\frac{1}{(x^{2}+1)^{6}}\,dx.\end{align*}
ポイントは
- $\dint_{-R}^{R}\frac{1}{(x^2+1)^6}\,dx$が$\dint_{C}f(z)\,dz$と$\dint_{C_R}f(z)\,dz$を用いて書ける
- $R>1$なら常に$\dint_{C}f(z)\,dz$は一定
- $\dint_{C_R}f(z)\,dz$は求められなくても，$R\to\infty$の極限は分かる
の３つです．これらを意識しながら解答を読み進めてください．
複素関数$f$と複素平面上の曲線$L_{R}$, $C_R$と閉曲線$C$を次で定めます：
\begin{align*}&f(z)=\dfrac{1}{(z^{2}+1)^{6}},
\\&L_R:=\set{z\in\R}{z=x,x\in[-R,R]},
\\&C_R:=\set{z\in\R}{z=R(\cos{t}+i\sin{t}),t\in[0,\pi]}
\\&C:=L_R\cup C_R\end{align*}
ただし，$R>1$とします．このとき，
\begin{align*}\int_{-R}^{R}\frac{1}{(x^{2}+1)^{6}}\,dx
&=\int_{L_{R}}f(z)\,dz
\\&=\int_{C}f(z)\,dz-\int_{C_{R}}f(z)\,dz\end{align*}
となりますね．
ステップ１（$C_R$上の積分）
$z\in C_{R}$に対して$\dfrac{dz}{dt}=R(-\sin{t}+i\cos{t})$だから，
\begin{align*}
\abs{\int_{C_{R}}f(z)\,dz}
&=\abs{\int_{0}^{\pi}\frac{R(-\sin{t}+i\cos{t})}{(R^{2}(\cos{2t}+i\sin{2t})+1)^{6}}\,dt}
\\&\le\int_{0}^{\pi}\frac{|R(-\sin{t}+i\cos{t})|}{|R^{2}(\cos{2t}+i\sin{2t})+1|^{6}}\,dt
\\&\le\int_{0}^{\pi}\frac{R}{(|R^{2}(\cos{2t}+i\sin{2t})|-1)^{6}}\,dt
\\&=\int_{0}^{\pi}\frac{R}{(R^{2}-1)^{6}}\,dt
=\frac{\pi R}{(R^{2}-1)^{6}}
\end{align*}
となり，$\lim\limits_{R\to\infty}\abs{\dint_{C_{R}}f(z)\,dz}=0$と計算できるので，$\lim\limits_{R\to\infty}\dint_{C_{R}}f(z)\,dz=0$が得られます．
ただし，下から２行目の不等式では三角不等式
\begin{align*}|R^{2}(\cos{2t}+i\sin{2t})+1|\ge|R^{2}(\cos{2t}+i\sin{2t})|-1\end{align*}
を用いました．
ステップ２（$C$上の積分と留数定理）
$f$は領域$\C\setminus\{\pm i\}$で正則で$R>1$だから，留数定理より
\begin{align*}\int_{C}f(z)\,dz=2\pi i\operatorname{Res}(f,i)\end{align*}
となります．
よって，
\begin{align*}\int_{-R}^{R}\frac{1}{(x^{2}+1)^{6}}\,dx
=2\pi i\operatorname{Res}(f,i)-\int_{C_{R}}f(z)\,dz\end{align*}
なので，極限$R\to\infty$をとればステップ１と併せて
\begin{align*}\int_{-\infty}^{\infty}\frac{1}{(x^{2}+1)^{6}}\,dx
=2\pi i\operatorname{Res}(f,i)\end{align*}
となります．よって，あとは留数$\operatorname{Res}(f,i)$を求めれば，問題の広義積分が得られますね．
ステップ３（留数を求める）
複素関数$g$を
\begin{align*}g(z):=(z-i)^6f(z)=\frac{1}{(z+i)^{6}}\end{align*}
で定めると，$g$は$i$の近傍の正則関数だから$i$でテイラー展開可能です．よって，
\begin{align*}&g(z)=c_{0}+c_{1}(z-i)+c_{2}(z-i)^{2}+\dots
\\&\iff f(z)=\frac{a_{0}}{(z-i)^{6}}+\dots+\frac{a_{5}}{z-i}+a_{6}+a_{7}(z-i)+\dots\end{align*}
と$f$は$i$でローラン展開可能で$\operatorname{Res}{(f,i)}=a_{5}$となりますね．このローラン展開から
\begin{align*}\frac{d^{5}g}{dz^{5}}(i)=5!a_{5}\end{align*}
であり，$g(z)=\dfrac{1}{(z+i)^{6}}$から
\begin{align*}\frac{d^{5}g}{dz^{5}}(z)
=\frac{(-6)(-7)\dots(-10)}{(z+i)^{11}}
=-\frac{10!}{5!(z+i)^{11}}\end{align*}
だから，
\begin{align*}\operatorname{Res}{(f,i)}
=a_{5}
=\frac{1}{5!}\cdot\frac{d^{5}g}{dz^{5}}(i)
=-\frac{10!}{(5!)^{2}(i+i)^{11}}
=\frac{10!}{(5!)^{2}2^{11}i}\end{align*}
が得られます．
よって，目的の広義積分は
\begin{align*}\int_{-\infty}^{\infty}\frac{1}{(x^{2}+1)^{6}}\,dx=\frac{10!}{(5!)^{2}2^{10}}\pi\end{align*}
と計算できました．
留数定理の証明
最後に留数定理を証明しましょう．留数定理は
の２つが理解できていれば簡単に導くことができます．
［留数定理（再掲）］領域$D$内に有限個の点$\alpha_{1},\dots,\alpha_{n}$があり，$D$内の閉曲線$C$がこれらの点を内部に含むとする．このとき，領域$D\setminus\{\alpha_{1},\dots,\alpha_{n}\}$上の正則関数$f$に対して
\begin{align*}\int_{C}f(z)\,dz=2\pi i\mrm{Res}(f,\alpha_{1})+\dots+2\pi i\mrm{Res}(f,\alpha_{n})\end{align*}
が成り立つ．ただし，$C$の向きは正方向とし，$\mrm{Res}(f,\alpha_{k})$は$f$の点$\alpha_{k}$での留数を表す（$k=1,\dots,n$）．
周も内部も$D$内に含まれる$\alpha_k$中心の円周$C_1,\dots,C_n$を，$C_1,\dots,C_n$が互いに外部にあるようにとる．
閉積分経路$C$を領域$D\setminus\{\alpha_{1},\dots,\alpha_{n}\}$内で連続的に変形して$C_1\cup\dots\cup C_n$に連続的に変形できるから，コーシーの積分定理より
\begin{align*}\int_{C}f(z)\,dz=\int_{C_1}f(z)\,dz+\dots+\int_{C_n}f(z)\,dz\end{align*}
である．$\dint_{C_k}f(z)\,dz=2\pi i\operatorname{Res}{(f,\alpha_k)}$（$k=1,2,\dots,n$）だから
\begin{align*}\int_{C}f(z)\,dz=2\pi i\mrm{Res}(f,\alpha_{1})+\dots+2\pi i\mrm{Res}(f,\alpha_{n})\end{align*}
が従う．
コメント