ルベーグ可測集合はルベーグ積分においてベースとなる集合たちです.
実用上の多くの$\R$の部分集合はルベーグ可測集合ですが,選択公理を仮定することでルベーグ可測集合でない集合の存在を証明することができます.
そのようなルベーグ非可測集合の最も代表的な例にヴィタリ集合があります.
この記事では
- 集合上の同値関係
- ヴィタリ集合の定義と存在
- ヴィタリ集合の非可測性
を順に解説します.
集合上の同値関係
最初に同値関係を踏まえておくと,ヴィタリ集合がどのような集合か理解しやすいでしょう.
集合上の関係の定義
まずは集合上の関係を定義します.
$\sim$が集合$X$上の関係であるとは,任意の$x,y\in X$に対して$x\sim y$であるか否かが定まるものをいう.
より正確には直積$X\times X$の部分集合として定義されますが,ここでは詳細は省略します.
例えば,整数全部の集合$\Z$上の関係$\sim$を
\begin{align*}x\sim y\overset{\mrm{def.}}{\iff}x-y\in3\Z\quad(x,y\in\Z)\end{align*}
と定めましょう.ただし,$3\Z$は3の倍数全部の集合です.
このとき,例えば
- $2-(-4)=6\in3\Z$なので$2\sim-4$
- $3-5=-2\notin3\Z$なので$3\nsim5$
というわけですね.
任意の$x,y\in\Z$に対して$x\sim y$であるか$x\not\sim y$であるかが定まるので,この$\sim$は$\Z$上の関係になっています.
集合上の同値関係の定義
集合上の関係で3つの性質[反射律][対称律][推移律]を満たすものを同値関係といいます.
集合$X$上の関係$\sim$が同値関係であるとは,次の3性質を満たすことをいう.
- [反射律]任意の$x\in X$は$x\sim x$を満たす
- [対称律]$x,y\in X$が$x\sim y$を満たすとき,$y\sim x$が成り立つ
- [推移律]$x,y,z\in X$が$x\sim y$かつ$y\sim z$を満たすとき,$x\sim z$が成り立つ
直観的には同値関係はグループ分けをしているのと同じことです.つまり,
- 反射律は$x$は$x$自身と同じグループ
- 対称律は$x$が$y$と同じグループなら,$y$は$x$と同じグループ
- 推移律は$x$が$y$と同じグループで,$y$が$z$と同じグループでなら,$x$は$z$と同じグループ
という性質になっているわけですね.
例えば,上の$\Z$上の関係
\begin{align*}x\sim y\overset{\mrm{def.}}{\iff}x-y\in3\Z\quad(x,y\in\Z)\end{align*}
は同値関係になっています.実際,
- 任意の$x\in\Z$に対して,$x-x=0\in3\Z$なので$x\sim x$を満たす
- $x,y\in\Z$が$x\sim y$を満たすとき,$y-x=-(x-y)\in3\Z$なので$y\sim x$が成り立つ
- $x,y,z\in\Z$が$x\sim y$かつ$y\sim z$を満たすとき,$x-z=(x-y)-(y-z)\in3\Z$なので$x\sim z$が成り立つ
なので,関係$\sim$は[反射律][対称律][推移律]を満たしますね.
同値類
直観的には集合上の同値関係は集合のグループ分けでしたから,これについて次のように定義します.
集合$X$上の同値関係$\sim$を考える.同値関係にある$X$の元をまとめてできる集合を同値類という.
また,同値類$C$に属する元を$C$の代表元という.
再び上の$\Z$上の同値関係
\begin{align*}x\sim y\overset{\mrm{def.}}{\iff}x-y\in3\Z\quad(x,y\in\Z)\end{align*}
を考えると,差が3の倍数の整数たちをまとめてひとつの同値類となります.よって,同値類は全部で
- $\{\dots,-6,-3,0,3,6,\dots\}$
- $\{\dots,-5,-2,1,4,7,\dots\}$
- $\{\dots,-4,-1,2,5,8,\dots\}$
の3つですね.
\def\xs{-3.5}\def\xl{3.5}
\draw[->,>=stealth,semithick](xs)node[left]{\color{blue}$\Z$}–(xl); %x軸
代数学的に言えば,可換群$(\N,+)$を部分群$(3\Z,+)$で割った剰余群$\Z/3\Z$を考えているわけですね.
一般に集合$X$の同値関係があったとき,$X$の全ての元はいずれかの同値類に属しますね.
ヴィタリ集合の定義と存在
次にヴィタリ集合を定義して,選択公理から存在を証明しましょう.
ヴィタリ集合の定義
次の性質をもつ集合$V\subset[0,1]$をヴィタリ集合(Vitali set)という:
- 任意の$x\in\R$に対して,ある$u\in V$と$r\in\Q$が存在して,$u+r=x$が成り立つ.
- 異なる$u,v\in V$に対して,$u+r=v$となる$r\in\Q$が存在しない.
(1), (2)を言葉で説明すると,それぞれ
- 任意の$x\in\R$がヴィタリ集合$V$の元の有理数分の平行移動で表せる
- ヴィタリ集合$V$のどの2元も有理数分の平行移動で移り合わない
ということですね.
ヴィタリ集合の存在
例えば「2つの内角が$90^\circ$の三角形を超直角三角形という」と勝手に定義しても,ユークリッド空間上ではそのような三角形は存在しません.
このように,何かを定義したとしてもそのようなものが本当に存在するかは別の話で,ヴィタリ集合も勝手に定義しているだけで本当は存在しないかもしれません.
しかし,選択公理を仮定すればヴィタリ集合の存在を証明することができます.
選択公理を仮定すれば,ヴィタリ集合は存在する.
ステップ1(同値関係)
実数全部の集合$\R$上の関係$\sim$を
\begin{align*}x\sim y\overset{\mrm{def.}}{\iff}x-y\in\Q\quad(x,y\in\R)\end{align*}
と定める.このとき,
- 任意の$x\in\R$に対して,$x-x=0\in\Q$なので$x\sim x$を満たす
- $x,y\in\R$が$x\sim y$を満たすとき,$y-x=-(x-y)\in\Q$なので$y\sim x$が成り立つ
- $x,y,z\in X$が$x\sim y$かつ$y\sim z$を満たすとき,$x-z=(x-y)-(y-z)\in\Q$なので$x\sim z$が成り立つ
と$\sim$は$\R$上の同値関係となる.
ステップ2($[0,1]$上の代表元)
同値関係$\sim$の任意の同値類$C$を考え,$\gamma\in C$をとる.$\Q$の$\R$上での稠密性より,
\begin{align*}\delta:=\gamma+r\in[0,1]\end{align*}
なる$r\in\Q$が存在する.このとき,$\delta-\gamma=r\in\Q$より$\delta\sim\gamma$なので,$C$は区間$[0,1]$上の代表元$\delta$をもつ.
よって,任意の同値類は$[0,1]$に属する代表元をもつ.
ステップ3(ヴィタリ集合の存在)
選択公理から全ての同値類$C$から$[0,1]$に属する代表元をとることができる.
それら全ての代表元を集めた集合を$V$とする.このとき,
- 任意の$x\in\R$はいずれかの同値類$C$に属するから,$V$は全ての同値類の代表元をもつ.よって,$x\sim\gamma$なる$\gamma\in V$が存在し,$x-\gamma\in\Q$が成り立つ.
- 異なる$u,v\in V$は異なる$\sim$の同値類の代表元だから,同値関係$\sim$の定義より$u-v\notin\Q$である.
だから,$V$はヴィタリ集合となっており,ヴィタリ集合の存在が示された.
可換群$(\R,+)$を部分群$(\Q,+)$で割った剰余群$\R/\Q$の各同値類から$[0,1]$に属する代表元を(選択公理を用いて)ひとつずつ取ってできる集合と言うことができます.
証明中の同値関係について,$x\in\R$が属する同値類$C_x$は
\begin{align*}C_x=\set{x+r}{r\in\Q}\end{align*}
と表せますね.この$C_x$は有理数全部の集合$\Q$をちょうど$+x$平行移動させた集合なので,$C_x$は可算集合となっています.
可算集合の濃度は$\R$の濃度よりも小さく,同値関係$\sim$によってできる同値類は無数に存在することが分かります.
そのような無数に存在する各同値類から$[0,1]$に属する代表元をひとつずつとってきてできる集合がヴィタリ集合というわけですね.
ヴィタリ集合の非可測性
最後にヴィタリ集合の非可測性を証明しましょう.
証明
ヴィタリ集合$V$はルベーグ可測集合でない.
$\Q\cap[-1,1]$は可算集合だから,$\Q\cap[-1,1]=\{r_1,r_2,\dots\}$と表せる.そこで,正の整数$n$に対して,
\begin{align*}V_n:=\set{v+r_n}{v\in V}\end{align*}
とおく.すなわち,$V_n$は$V$を有理数$r_n$だけ平行移動してできる集合である.
ステップ1(共通部分$V_n\cap V_m$)
$m\neq n$なら$V_n\cap V_m=\emptyset$であることを背理法により示す.
もし$x\in V_n\cap V_m$が存在すれば,$x=v+r_n$, $x=v’+r_m$なる$v,v’\in V$が存在するので,辺々引いて整理すると
\begin{align*}v-v’=r_m-r_n\in\Q\end{align*}
となり$v\sim v’$を得る($\sim$は上の命題の証明中の同値関係).
いま$V$は各同値類からひとつずつ代表元をとってできる集合だから$v=v’$でなければならないが,このとき
\begin{align*}0=r_m-r_n\iff r_m=r_n\iff m=n\end{align*}
を得る.これは$m\neq n$に矛盾するから,仮定は誤りで$V_n\cap V_m=\emptyset$が成り立つ.
ステップ2($V_n$の和集合の包含関係)
集合の包含$[0,1]\subset\bigcup\limits_{n=1}^{\infty}V_n\subset[-1,2]$を示す.
任意の$n$に対して$r_n\in[-1,1]$だから,$V\in[0,1]$と併せて$V_n\subset[-1,2]$である.よって,$\bigcup\limits_{n=1}^{\infty}V_n\subset[-1,2]$を得る.
また,任意に$x\in[0,1]$をとる.$V$は各同値類からひとつずつ代表元をとってできる集合だから,ある$v\in V$と$r\in\Q$が一意に存在して$r=x-v$が成り立つ.
いま$V\subset[0,1]$に注意すると$r=x-v\in[-1,1]$なので,ある$n$が一意に存在して
\begin{align*}x=v+r_n\in V_n\end{align*}
が成り立つ.よって,$[0,1]\subset\bigcup\limits_{n=1}^{\infty}V_n$を得る.
ステップ3(ヴィタリ集合の非可測性)
ヴィタリ集合$V$がルベーグ可測集合でないことを背理法により示す.
もしヴィタリ集合$V$がルベーグ可測集合なら,$V$を平行移動してできる$V_n$もルベーグ可測集合で,それらの可算個の和集合$\bigcup\limits_{n=1}^{\infty}V_n$もルベーグ可測集合である.
また,一般に区間はルベーグ可測集合なので,$[0,1]$と$[-2,1]$はルベーグ可測集合である.
\begin{align*}1\le m\bra{\bigcup_{n=1}^{\infty}V_n}\le3\quad\dots(*)\end{align*}
が成り立つ.ステップ1とルベーグ測度$m$の完全加法性と平行移動不変性より
\begin{align*}m\bra{\bigcup_{n=1}^{\infty}V_n}=\sum_{n=1}^{\infty}m(V_n)=\sum_{n=1}^{\infty}m(V)\end{align*}
である.$m(V)$は非負定数で
- $m(V)=0$なら$\sum\limits_{n=1}^{\infty}m(V)=0$
- $m(V)>0$なら$\sum\limits_{n=1}^{\infty}m(V)=\infty$
なので,これは$(*)$に矛盾するから仮定は誤りで,ヴィタリ集合$V$はルベーグ可測集合でない.
ルベーグ可測集合でなければルベーグ測度$m$の定義域に属していないため,$m$の完全加法性が使えません(ルベーグ外測度は完全加法性を持ちません).
そのため,一旦ヴィタリ集合をルベーグ可測集合と仮定することで,本来は使えないはずの完全加法性を使うことで矛盾が導かれるわけですね.
ルベーグ外測度の不具合
ヴィタリ集合$V$の存在により,次のことが言えますね.
$A\cap B=\emptyset$かつ$m^{*}(A\cup B)\neq m^{*}(A)+m^{*}(B)$を満たす$A,B\subset\R$が存在する.ただし,$m^{*}$はルベーグ外測度である.
ヴィタリ集合$V$はルベーグ可測集合でないから,ある集合$X\subset\R$が存在して
\begin{align*}m^{*}(X)\neq m^{*}(X\cap V)+m^{*}(X\cap V^c)\end{align*}
が成り立つ.よって,$A=X\cap V$, $B=X\cap V^c$とすれば,
\begin{align*}X=X\cap(V\cup V^c)=(X\cap V)\cup(X\cap V^c)=A\cup B\end{align*}
なので,$m^{*}(A\cup B)\neq m^{*}(A)+m^{*}(B)$が成り立つ.
これによりルベーグ外測度$m^{*}$は完全加法性を満たさないため,測度論的にはルベーグ外測度$m^{*}$は測度といえないわけですね.

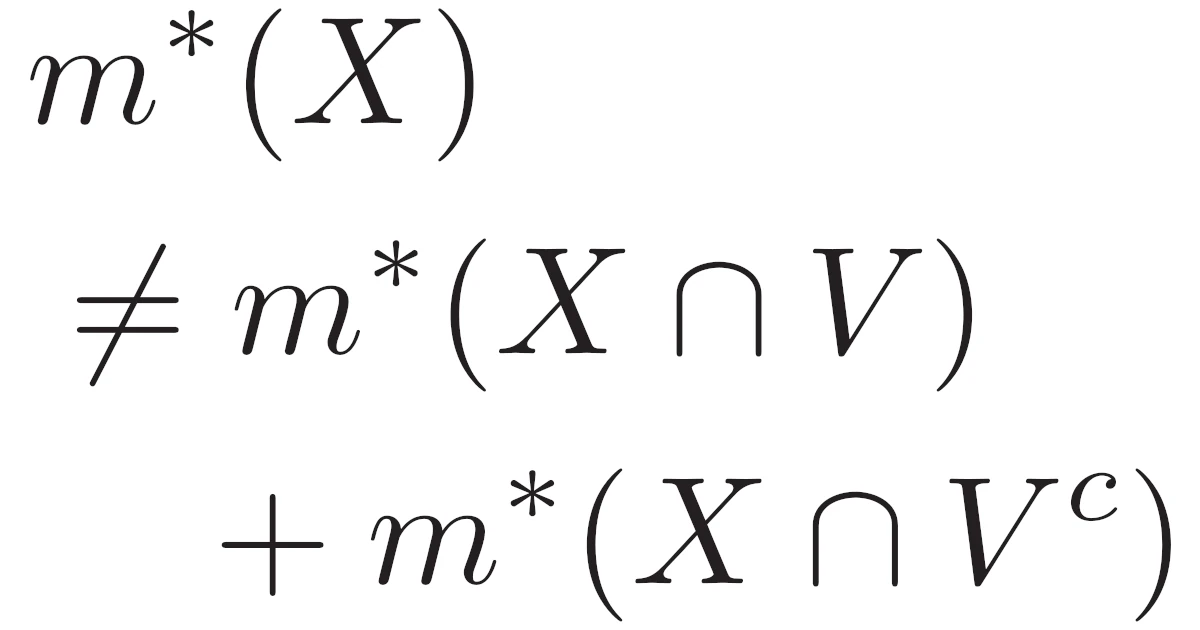


コメント