 位相空間論
位相空間論 商集合の考え方と具体例|同値関係はただのグループ分け
集合論には二項関係という概念がありますが,二項関係の中でもある性質を満たすものを同値関係といいます.最初に「同値関係」と聞くと語感からキツい印象を受けてしまいますが,実際にはただの「グループ分け」の考え方を数学的に定式化したものにほかなりま...
 位相空間論
位相空間論 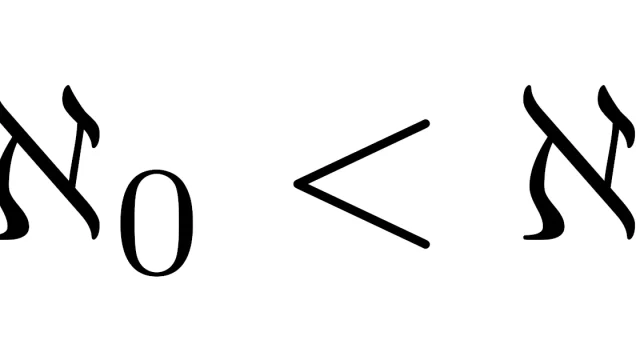 集合論
集合論 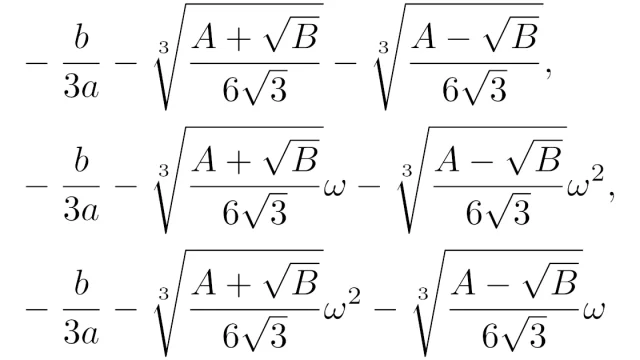 代数学
代数学  微分積分学
微分積分学  関数空間
関数空間  位相空間論
位相空間論 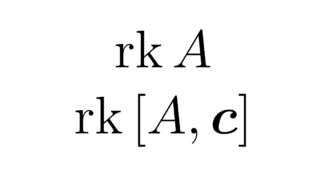 線形代数学の基本
線形代数学の基本 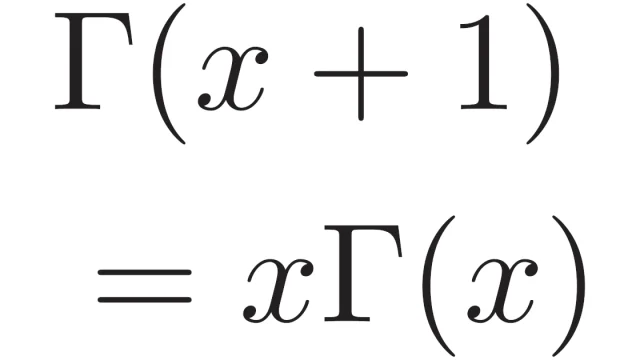 微分積分学
微分積分学 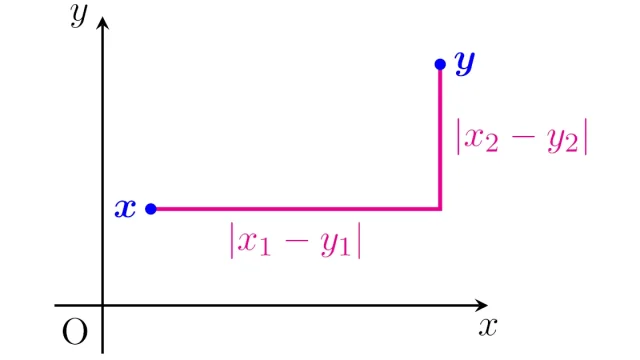 位相空間論
位相空間論 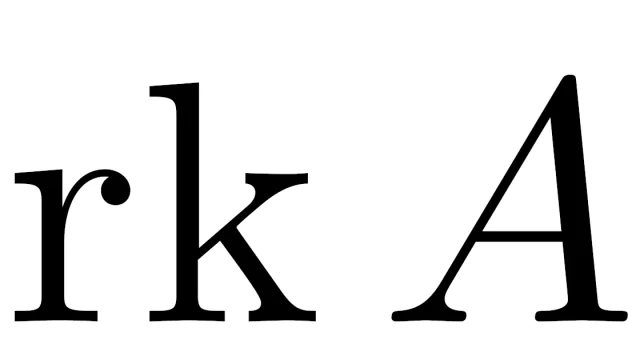 線形代数学の基本
線形代数学の基本