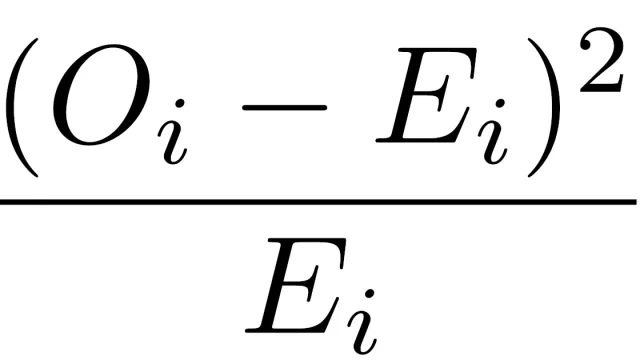 仮説検定
仮説検定 カイ二乗適合度検定を具体例から理解する|理論の証明も解説
3つの事象A, B, Cのいずれかが起こる試行について,それぞれが起こる確率が想定されているとします.この想定が正しいかどうかを確認する仮説検定としてカイ二乗適合度検定がよく用いられます.
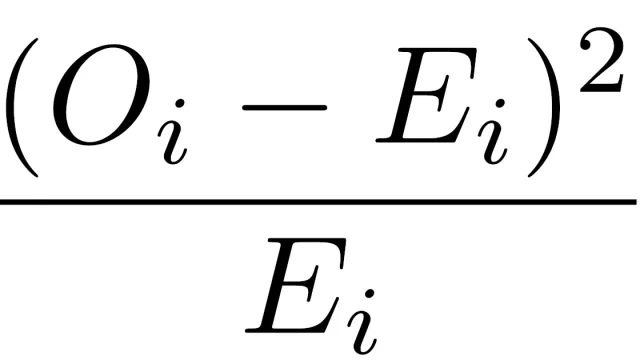 仮説検定
仮説検定 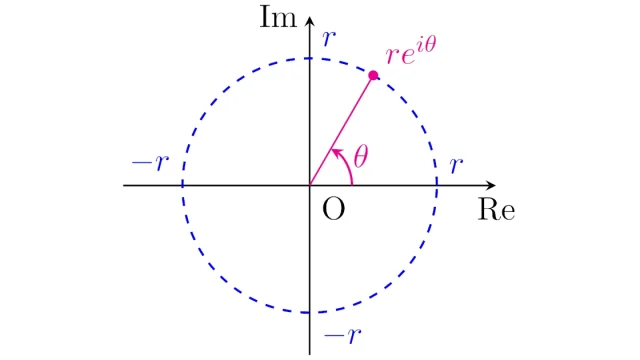 複素解析の基本
複素解析の基本 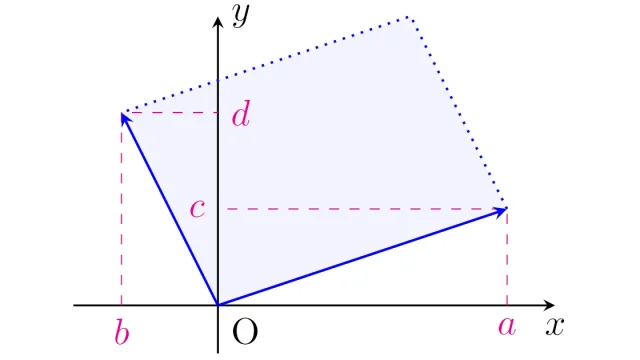 線形代数学
線形代数学 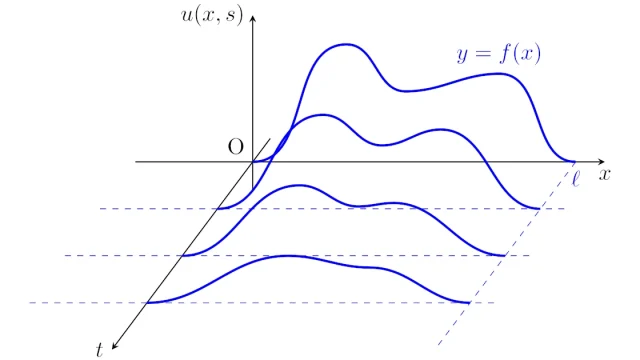 偏微分方程式
偏微分方程式 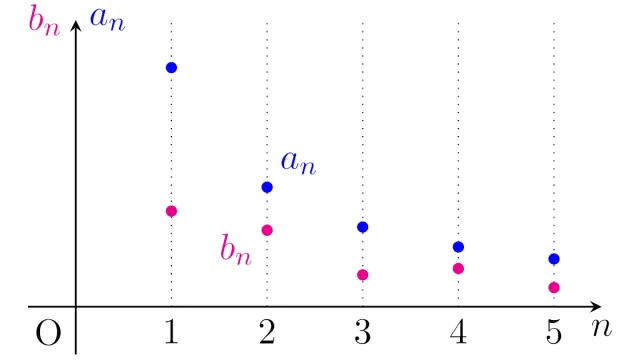 微分積分学の基本
微分積分学の基本 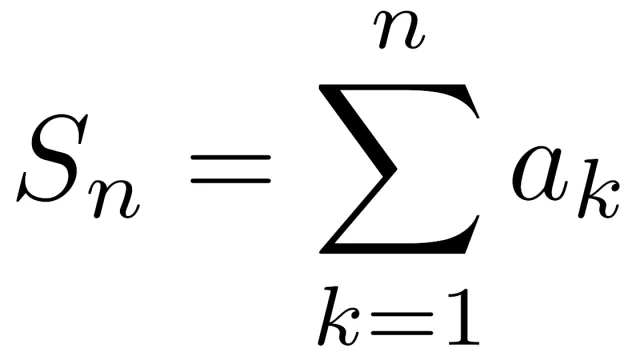 微分積分学の基本
微分積分学の基本 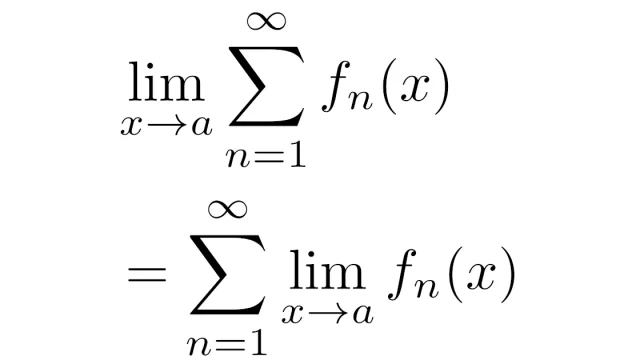 測度論
測度論 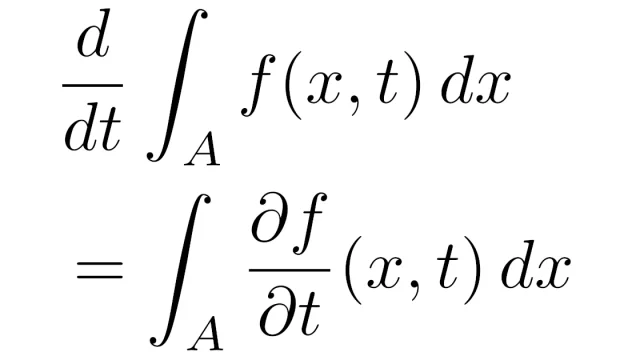 ルベーグ積分の基本
ルベーグ積分の基本 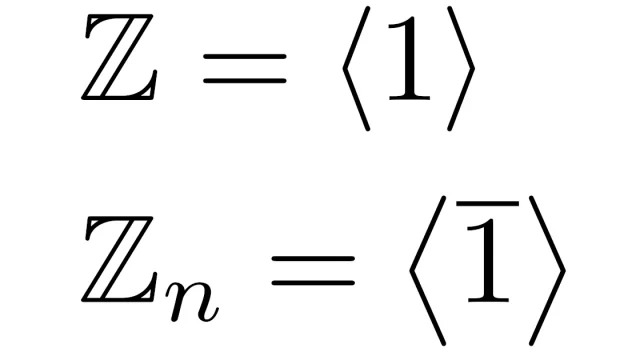 群論の基本
群論の基本  複素解析
複素解析