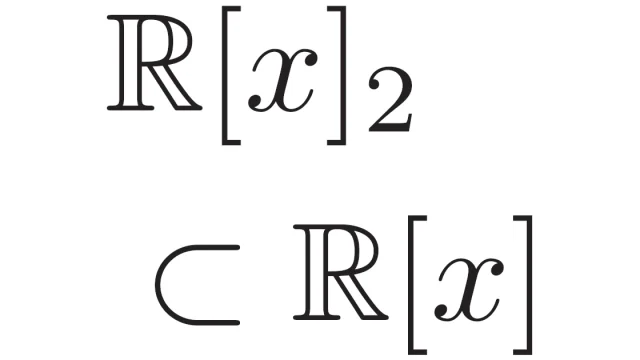 線形空間の基本
線形空間の基本 線形部分空間の定義|証明のテンプレートも例題に沿って紹介
線形空間Vの部分集合UがVの和とスカラー倍について閉じているとき,UをVの線形部分空間といいます.この記事では線形部分空間の定義と証明のテンプレートを紹介し,基本性質を証明します
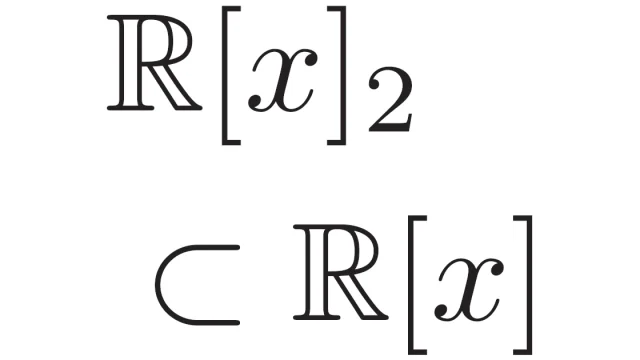 線形空間の基本
線形空間の基本 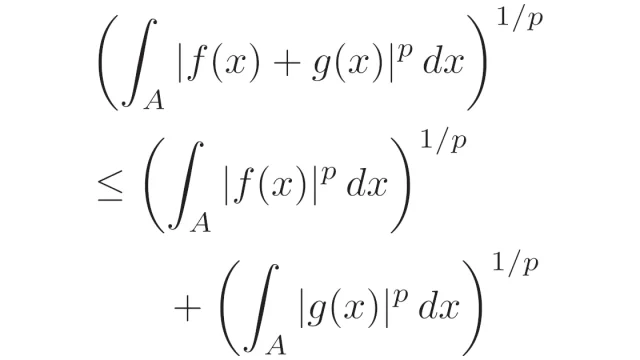 ルベーグ空間
ルベーグ空間 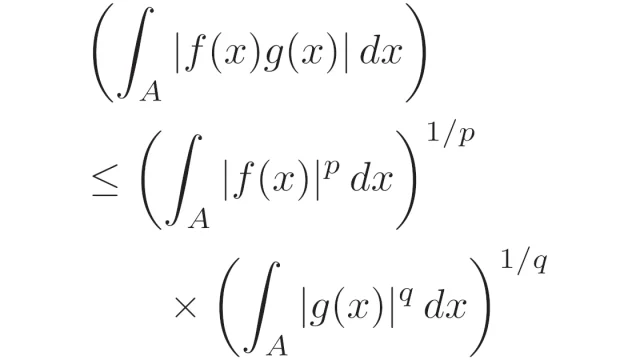 ルベーグ空間
ルベーグ空間 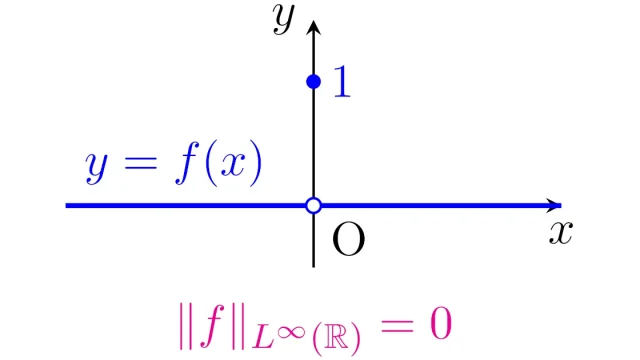 ルベーグ空間
ルベーグ空間 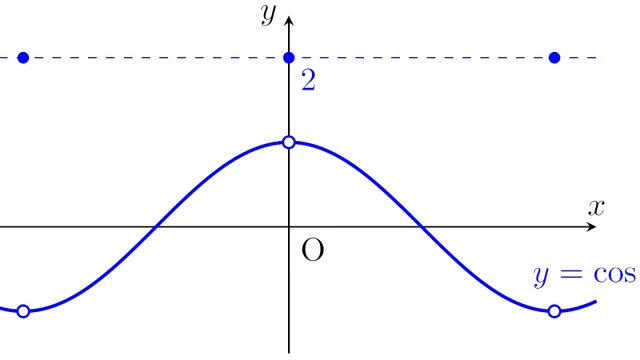 ルベーグ空間
ルベーグ空間 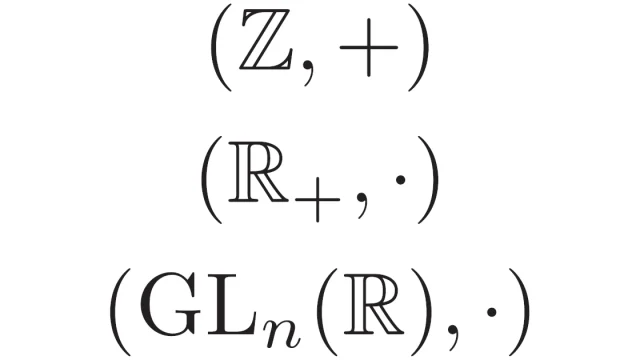 群論の基本
群論の基本 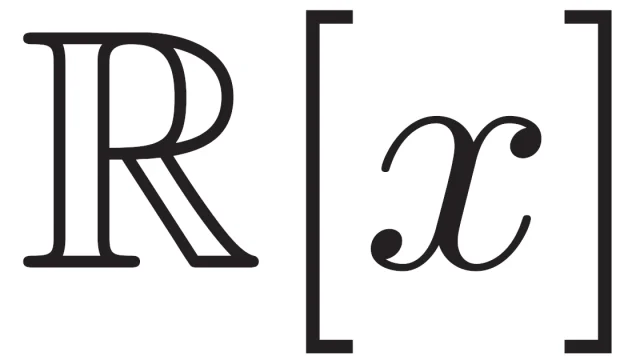 線形空間の基本
線形空間の基本 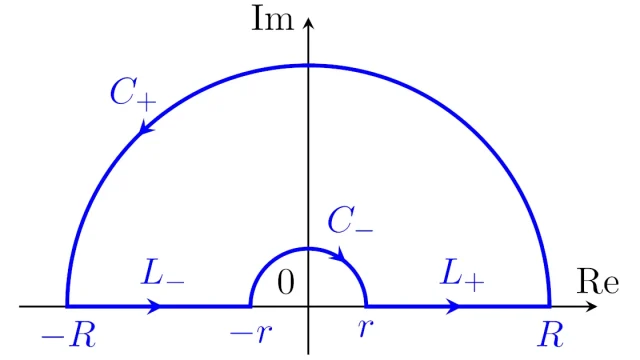 複素解析
複素解析 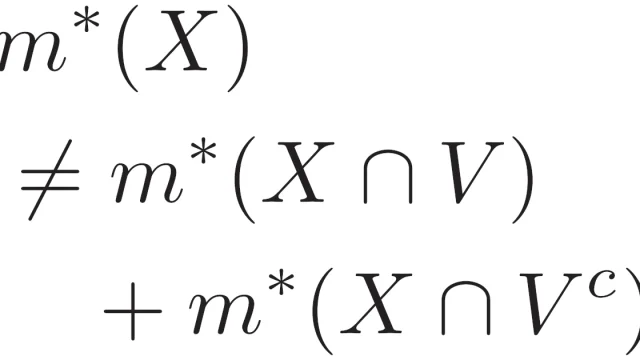 ルベーグ積分
ルベーグ積分 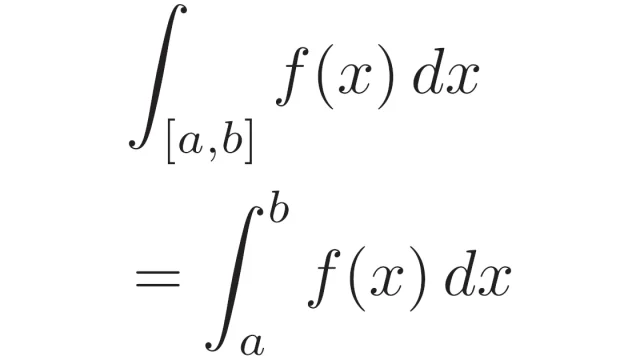 ルベーグ積分の基本
ルベーグ積分の基本