 ルベーグ積分の基本
ルベーグ積分の基本 ルベーグの優収束定理の3つのポイント|定理の証明と具体例
ルベーグ積分は極限と相性が良く,その中でも積分と極限が順序交換であることを保証する「ルベーグの優収束定理」は非常に便利で広く用いられます.この記事ではルベーグの優収束定理の使い方を例題をもとに解説し,定理の証明をします.
 ルベーグ積分の基本
ルベーグ積分の基本  ルベーグ積分の基本
ルベーグ積分の基本  ルベーグ積分の基本
ルベーグ積分の基本  ルベーグ積分の基本
ルベーグ積分の基本 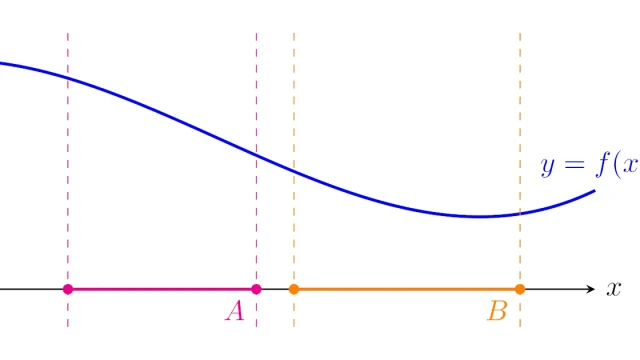 ルベーグ積分の基本
ルベーグ積分の基本 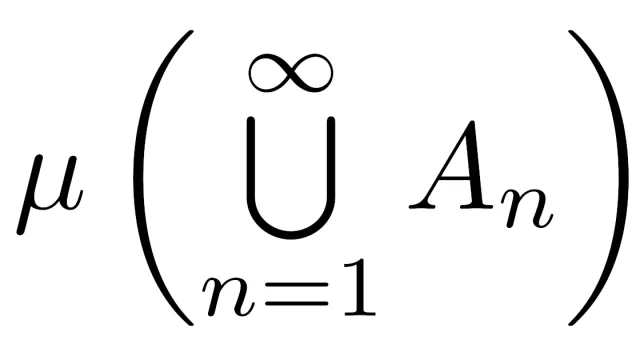 測度論
測度論 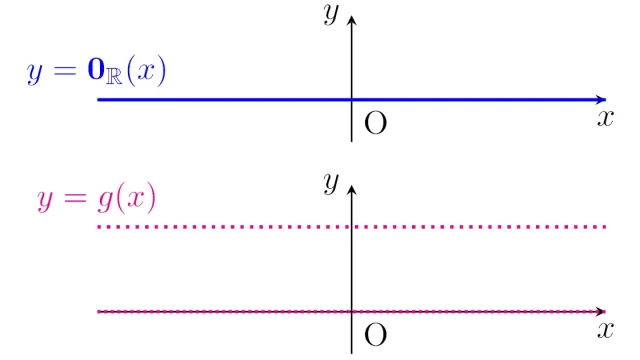 測度論
測度論 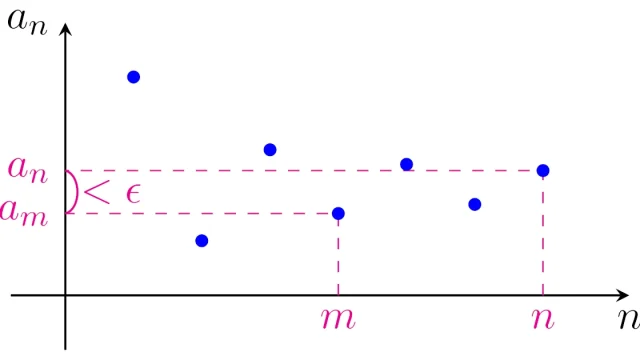 微分積分学の基本
微分積分学の基本  微分積分学の基本
微分積分学の基本  測度論
測度論