フーリエ変換は「関数を波の和で表す」という発想に基づいた変換であり,理工系の様々な分野で重宝されています.また,
\begin{align*}G(x)=Ae^{-\frac{(x-\mu)^2}{2\sigma^2}}\end{align*}
で定まる関数$G:\R\to\R$を1次元のガウス(Gauss)関数といいます.
このガウス関数$G$は確率・統計の分野では,$A=\frac{1}{\sqrt{2\pi\sigma^2}}$のとき平均$\mu$,分散$\sigma^2$の正規分布の確率密度関数としても有名ですね.
$\mu=0$の場合のガウス関数には,フーリエ変換を施しても再び$\mu=0$のガウス関数になるという性質があります.
詳しくは,$G(x)=e^{-\eta x^2}$で定まるガウス関数$G:\R\to\R$のフーリエ変換は
\begin{align*}\mathcal{F}[G](\xi)=\frac{1}{\sqrt{2\eta}}\exp\bra{-\frac{\xi^2}{4\eta}}\end{align*}
となります.
この記事では
- フーリエ変換とガウス関数
- ガウス関数のフーリエ変換がガウス関数であることの証明
- 微分方程式による求め方
を順に解説します.
なお,微分方程式を解くことでガウス関数のフーリエ変換を計算する方法もあり,この方法については以下の記事を参照してください.

フーリエ変換とガウス関数
まずはこの記事の主役であるフーリエ変換とガウス関数の基本を確認しておきましょう.
フーリエ変換の定義
形式的に,関数$f$のフーリエ変換は
\begin{align*}\frac{1}{\sqrt{2\pi}}\int_{\R}f(x)e^{-ix\xi}\,dx\end{align*}
で定義されます.
性質の良くない関数$f$に対してはフーリエ変換が定義できないこともありますが,簡単な目安としてルベーグ積分可能な関数$f$に対してはフーリエ変換が定義できます.
ルベーグ積分を知らない方はリーマン積分と思っていても,この記事の本題に大きな影響はありません.
実際,ルベーグ可積分なルベーグ可測関数$f$, $\xi\in\R$に対して
\begin{align*}\int_{\R}|f(x)e^{-ix\xi}|\,dx=\int_{\R}|f(x)|\,dx<\infty\end{align*}
なので,$\dint_{\R}|f(x)e^{-ix\xi}|\,dx$が有限の値として存在し,$\dint_{\R}f(x)e^{-ix\xi}\,dx$も有限の値として存在することが分かりますね.
[フーリエ変換(1変数)]$\R$上の可積分関数$f$に対して,フーリエ変換$\mathcal{F}$を
\begin{align*}\mathcal{F}_{x}[f](\xi)=\frac{1}{\sqrt{2\pi}}\int_{\R}e^{-ix\xi}f(x)\,dx\end{align*}
で定義する.
フーリエ変換$\mathcal{F}_{x}[f]$は$\hat{f}$と表記することもよくあります.
ガウス関数とガウス積分
冒頭でも説明したように,一般のガウス関数$G:\R\to\R$は
\begin{align*}G(x)=Ae^{-\frac{(x-\mu)^2}{2\sigma^2}}\end{align*}
ですが,この記事では$\eta>0$として
\begin{align*}G(x):=e^{-\eta x^2}\end{align*}
の形のガウス関数をフーリエ変換します.
さらに$\eta=1$の場合は$G(x):=e^{-x^2}$となりますが,このときの$G$の$\R$上の積分をガウス積分といい,
\begin{align*}\int_{\R}e^{-x^2}\,dx=\sqrt{\pi}\end{align*}
と計算されることがよく知られていますね.
ガウス関数とフーリエ変換
いま説明したガウス積分と,変数変換$y=\sqrt{\eta}x$より
\begin{align*}\int_{\R}G(x)\,dx&=\int_{\R}e^{-\eta x^2}\,dx
\\&=\frac{1}{\sqrt{\eta}}\int_{\R}e^{-y^2}\,dy=\sqrt{\frac{\pi}{\eta}}\end{align*}
となって$G$は可積分と分かるので,ガウス関数$G$のフーリエ変換は問題なく定義できますね.
ただ,ガウス積分の値が$\sqrt{\pi}$であることを知らなくても,$G$が可積分であることを示すだけであれば難しくありません.
定数$\eta>0$に対して,$G(x)=e^{-\eta x^2}$で定まる関数$G:\R\to\R$は可積分関数である.
$x\to\pm\infty$で負冪の指数関数は多項式の逆数よりも早く減衰するから,ある$R>0$が存在して,$|x|\ge R$なら
\begin{align*}x^2G(x)<1
\iff G(x)<\frac{1}{x^2}\end{align*}
が成り立つ.
また,任意の$x\in\R$に対して(したがって$x\in[0,R]$に対して),$e^{-\eta x^2}\le1$だから
\begin{align*}\int_{\R}|G(x)|\,dx
&=2\int_{0}^{\infty}|G(x)|\,dx
\\&=2\int_{0}^{R}|G(x)|\,dx+2\int_{R}^{\infty}|G(x)|\,dx
\\&=2\int_{0}^{R}\,dx+\int_{R}^{\infty}\frac{1}{x^2}\,dx
\\&=\frac{2}{R}+2R
<\infty\end{align*}
となるから,$G$は可積分関数である.
ガウス関数のフーリエ変換がガウス関数であることの証明
まず1変数のガウス関数のフーリエ変換を計算し,その結果を用いて多変数のガウス関数のフーリエ変換を計算しましょう.
1変数の場合のガウス関数のフーリエ変換
定数$\eta>0$に対して,$G(x):=e^{-\eta x^2}$で定まるガウス関数$G:\R\to\R$のフーリエ変換は
\begin{align*}\mathcal{F}[G](\xi)=\frac{1}{\sqrt{2\eta}}\exp\bra{-\frac{\xi^2}{4\eta}}\end{align*}
と再びガウス関数になる.
$\eta=\dfrac{1}{2}$のときは$\mathcal{F}[G]=G$とガウス関数の形までも不変ですね.
フーリエ変換の定義より
\begin{align*}\mathcal{F}[G](\xi)
=\frac{1}{\sqrt{2\pi}}\int_{\R}e^{-ix\xi}G(x)\,dx
=\frac{1}{\sqrt{2\pi}}\int_{\R}e^{-\eta x^2-ix\xi}\,dx\end{align*}
である.被積分関数の冪の部分は$x$に関して
\begin{align*}-\eta x^2-ix\xi=-\eta\bra{x+\frac{\xi}{2\eta}i}^2-\frac{\xi^2}{4\eta}\end{align*}
と平方完成できるから,$\lambda:=\frac{\xi}{2\eta}\in\R$とおくと
\begin{align*}\mathcal{F}[G](\xi)=\frac{1}{\sqrt{2\pi}}\exp\bra{-\frac{\xi^2}{4\eta}}\int_{\R}e^{-\eta(x+i\lambda)^2}\,dx\end{align*}
となる.あとは$\dint_{\R}e^{-\eta(x+i\lambda)^2}\,dx=\sqrt{\frac{\pi}{\eta}}$を示せばよい.
複素関数と積分経路
複素関数$f$を$f(z)=e^{-\eta z^2}$で定め,$R>0$を任意にとる.$\lambda>0(\iff\xi>0)$のとき4つの経路$L$, $L’$, $L_{R}$, $L_{-R}$を
\begin{align*}&L:=\set{z\in\C}{z=x,x\in[-R,R]},
\\&L’:=\set{z\in\C}{z=x+i\lambda,x\in[-R,R]},
\\&L_{R}:=\set{z\in\C}{z=R+iy,y\in[0,\lambda]},
\\&L_{-R}:=\set{z\in\C}{z=-R+i(\lambda-y),y\in[0,\lambda]}\end{align*}
で定める.
$\lambda<0(\iff\xi<0)$のときも同様に下図のように4つの経路$L$, $L’$, $L_{R}$, $L_{-R}$を定める.
いずれの場合も$\dint_{\R}e^{-\eta(x+i\lambda)^2}\,dx=\lim_{R\to\infty}\int_{L}f(z)\,dz$である.
全体の積分と$L_{\pm R}$上の積分
$f$は$\C$上の正則関数で$L’\cup L_{-R}\cup L\cup L_{R}$は閉曲線だから,コーシーの積分定理より
\begin{align*}\dint_{L’\cup L_{-R}\cup L\cup L_{R}}f(z)\,dz=0\end{align*}
が成り立つ.よって,
\begin{align*}\int_{\R}e^{-\eta(x+i\lambda)^2}\,dx&=\lim_{R\to\infty}\bra{-\int_{L’}f(z)\,dz}
\\&=\lim_{R\to\infty}\int_{L_{R}\cup L\cup L_{R}}f(z)\,dz\end{align*}
が成り立つ.また
\begin{align*}\abs{\int_{L_{R}}f(z)\,dz}&=\abs{\int_{0}^{\lambda}e^{-\eta (R+yi)^2}\,idy}\le\int_0^{\lambda}\abs{e^{-\eta(R+iy)^2}}\,|dy|
\\&=\int_0^{\lambda}\abs{e^{-\eta(R^2+2iRy-y^2)}}\,|dy|
\\&=\int_0^{\lambda}e^{-\eta(R^2-y^2)}\,|dy|\le\int_0^{\lambda}e^{-\eta R^2}\,|dy|
\\&=|\lambda|e^{-\eta R^2}\to0\quad (R\to\infty)\end{align*}
だから$\lim\limits_{R\to\infty}\dint_{L_{R}}f(z)\,dz=0$が成り立ち,同様に
\begin{align*}\abs{\int_{L_{-R}}f(z)\,dz}&=\abs{\int_0^{\lambda}e^{-\eta(-R+i(\lambda-y))^2}\,(-i)dy}\le\int_0^{\lambda}\abs{e^{-\eta(-R+i(\lambda-y))^2}}\,|dy|
\\&=\int_0^{\lambda}\abs{e^{-\eta(R^2+2i(\lambda-y)-(\lambda-y)^2)}}\,|dy|
\\&=\int_0^{\lambda}e^{-\eta(R^2-(\lambda-y)^2)}\,|dy|\le\int_0^{\lambda}e^{-\eta R^2}\,|dy|
\\&=|\lambda| e^{-\eta R^2}\to0\quad (R\to\infty)\end{align*}
だから$\lim\limits_{R\to\infty}\dint_{L_{-R}}f(z)\,dz=0$が成り立つ.
ガウス関数のフーリエ変換$\mathcal{F}[G]$
よって,(変数変換$x=\dfrac{y}{\sqrt{\eta}}$を用いて)ガウス積分と併せて
\begin{align*}\int_{\R}e^{-\eta(x+i\lambda)^2}\,dx&=\lim_{R\to\infty}\int_{L}f(z)\,dz
\\&=\int_{\R}e^{-\eta x^2}\,dx=\sqrt{\frac{\pi}{\eta}}\end{align*}
が従う.以上より,
\begin{align*}\mathcal{F}[G](\xi)&=\frac{1}{\sqrt{2\pi}}\dint_{\R}e^{-ix\xi}G(x)\,dx
\\&=\frac{1}{\sqrt{2\pi}}\cdot\exp\bra{-\frac{\xi^2}{4\eta}}\sqrt{\frac{\pi}{\eta}}
\\&=\frac{1}{\sqrt{2\eta}}\exp\bra{-\frac{\xi^2}{4\eta}}\end{align*}
となって,確かにガウス関数のフーリエ変換はガウス関数である.
多変数の場合のガウス関数のフーリエ変換
多変数の場合のフーリエ変換は以下の通りです.
[フーリエ変換(多変数)]$\R^N$上の可積分関数$f$に対して,フーリエ変換$\mathcal{F}$を
\begin{align*}\mathcal{F}_{x}[f](\xi)=\frac{1}{(2\pi)^{N/2}}\int_{\R^N}e^{-ix\cdot\xi}f(x)\,dx\end{align*}
で定義する.ただし,$x\cdot\xi$は$x\in\R^N$と$\xi\in\R^N$の標準内積である.
多変数のガウス関数$G$を
\begin{align*}G(x)=e^{-\eta|x|^2} (\eta>0)\end{align*}
としましょう($\eta>0$は定数).ただし,$x=[x_1,\dots,x_N]^T\in\R^N$であり,$|x|^2={x_1}^2+\dots+{x_N}^2$です.
このとき,ガウス関数$G$のフーリエ変換$\mathcal{F}[G]$は,1変数の場合の結果を用いて
\begin{align*}\mathcal{F}[G](\xi)
=&\frac{1}{(2\pi)^{N/2}}\int_{\R^N}e^{-ix\cdot\xi}G(x)\,dx
\\=&\frac{1}{(2\pi)^{N/2}}\int_{\R^N}\prod_{n=1}^Ne^{-ix_n\xi_n}\exp\bra{-\eta{x_n}^2}\,dx
\\=&\frac{1}{(2\pi)^{N/2}}\prod_{n=1}^N\dint_{\R}e^{-ix_n\xi_n}\exp\bra{-\eta{x_n}^2}\,dx_n
\\=&\frac{1}{(2\pi)^{N/2}}\prod_{n=1}^N\bra{\exp\bra{-\frac{{\xi_n}^2}{4\eta}}\sqrt{\frac{\pi}{\eta}}}
\\=&\frac{1}{(2\eta)^{N/2}}\exp\bra{-\frac{|\xi|^2}{4\eta}}\end{align*}
となって,確かにガウス関数のフーリエ変換がガウス関数であることが分かりました.
多変数の場合も$\eta=\dfrac{1}{2}$であれば$\mathcal{F}[G]=G$となりますね.
微分方程式による求め方
冒頭でも紹介しましたが,微分方程式を解くことで求める方法もあります.
これはガウス関数$G(x)=A\exp{\bigl(-\frac{x^2}{2\sigma^2}\bigl)}$のフーリエ変換$\mathcal{F}[G]$が,未知関数$u$, 変数$t$の微分方程式の初期値問題
\begin{align*}\begin{cases}\od{u}{t}(t)+\sigma^2tu(t)=0\\
u(0)=A\sigma\end{cases}\end{align*}
の解となることを示し,実際にこの微分方程式を解くことで求める方法です.
この方法については以下の記事を参照してください.


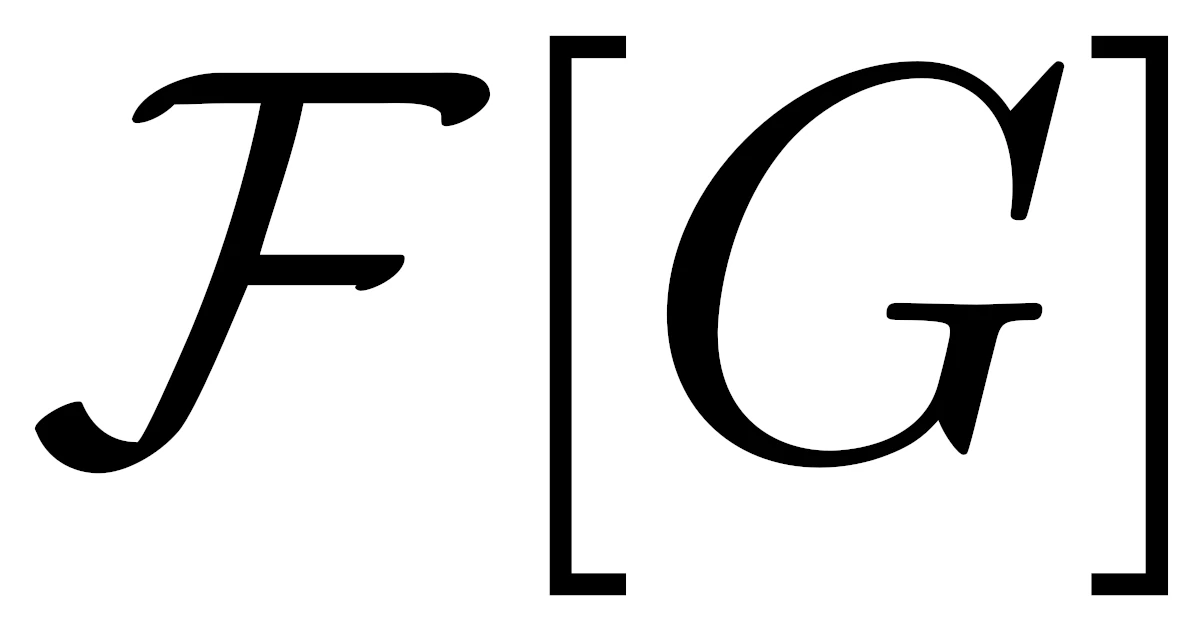
コメント