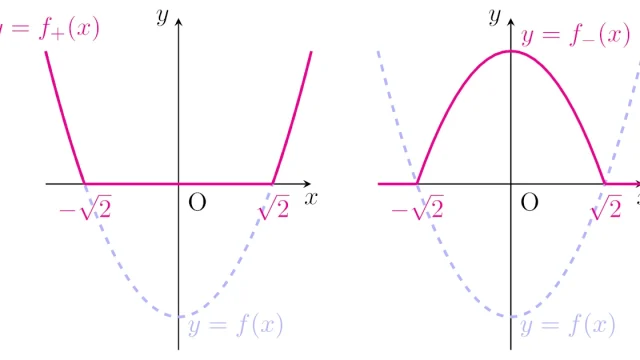
 ルベーグ積分の基本
ルベーグ積分の基本 線形結合・絶対値・連続関数などのルベーグ可測性を証明
ルベーグ積分はルベーグ可測関数に対して定義されるため,ルベーグ可測関数の性質を整理しておくことは大切です.この記事では,可測関数の線形結合・積・商・正成分・負成分・絶対値の可測性を証明します.
 ルベーグ積分の基本
ルベーグ積分の基本 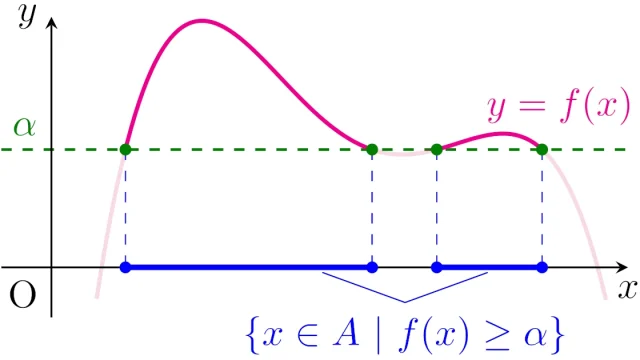 ルベーグ積分の基本
ルベーグ積分の基本 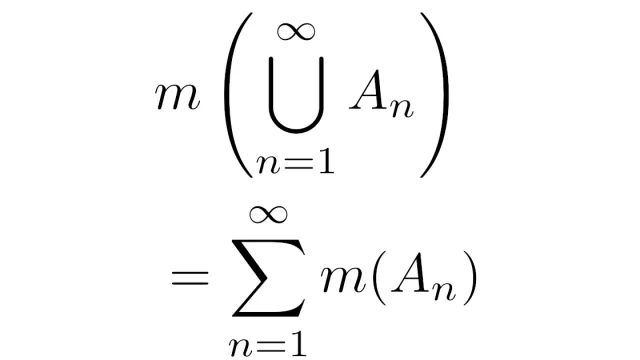 ルベーグ積分の基本
ルベーグ積分の基本 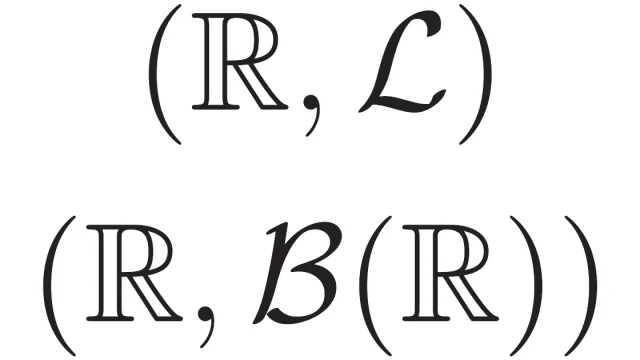 ルベーグ積分の基本
ルベーグ積分の基本 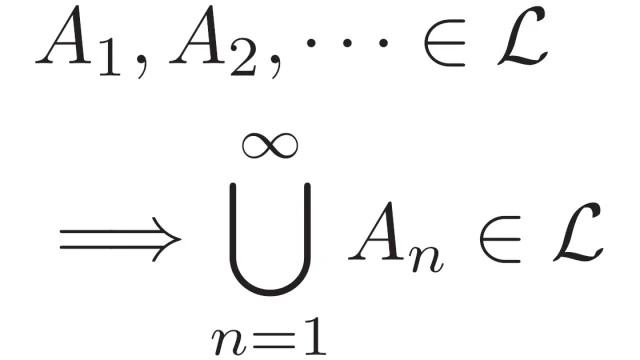 ルベーグ積分の基本
ルベーグ積分の基本 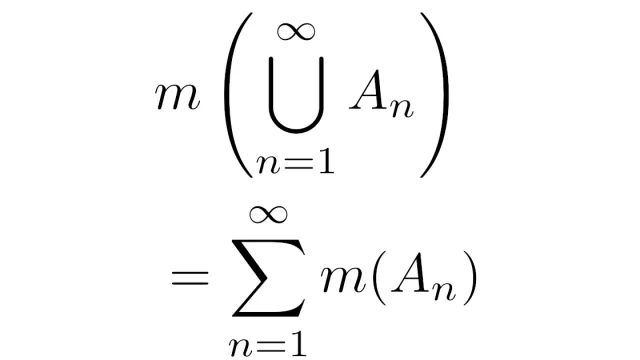 ルベーグ積分の基本
ルベーグ積分の基本 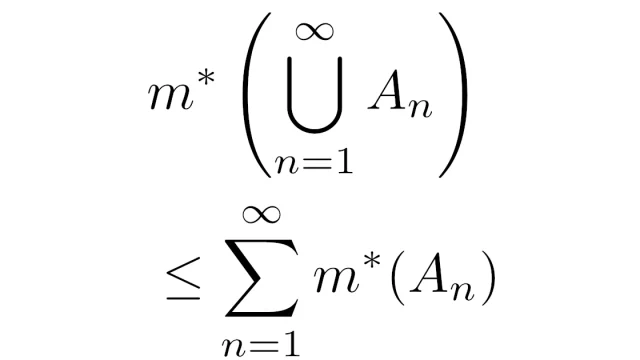 ルベーグ積分の基本
ルベーグ積分の基本  ルベーグ積分の基本
ルベーグ積分の基本 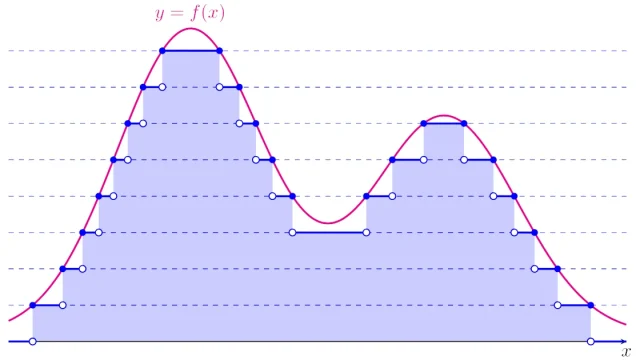 ルベーグ積分の基本
ルベーグ積分の基本