 微分積分学の基本
微分積分学の基本 収束しない実数列|実数列の3種類の発散と証明の例題
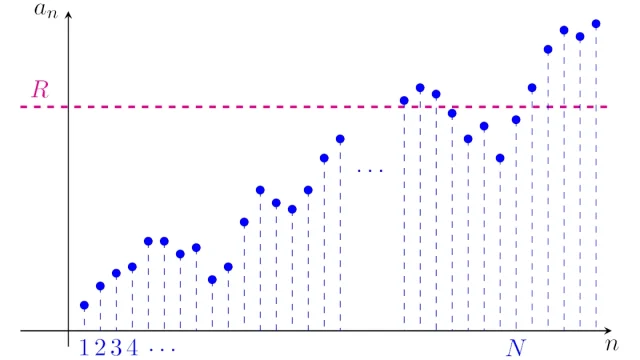
実数列{aₙ}が収束しないとき{aₙ}は発散するといいますが,発散には「∞に発散」「-∞に発散」「振動」の3種類があります.この記事では,これらの定義を厳密に扱い,具体例から証明の考え方も説明します.
 微分積分学の基本
微分積分学の基本  微分積分学
微分積分学  微分積分学
微分積分学  微分積分学の基本
微分積分学の基本  微分積分学
微分積分学  微分積分学
微分積分学  微分積分学の基本
微分積分学の基本  微分積分学
微分積分学  微分積分学
微分積分学 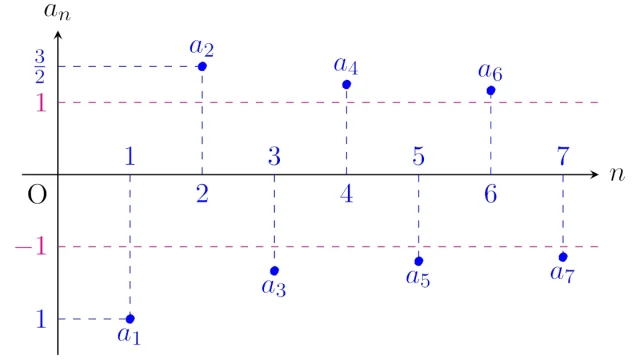 微分積分学
微分積分学