 線形代数学の基本
線形代数学の基本 固有値・固有ベクトルの求め方|固有方程式から2ステップで!
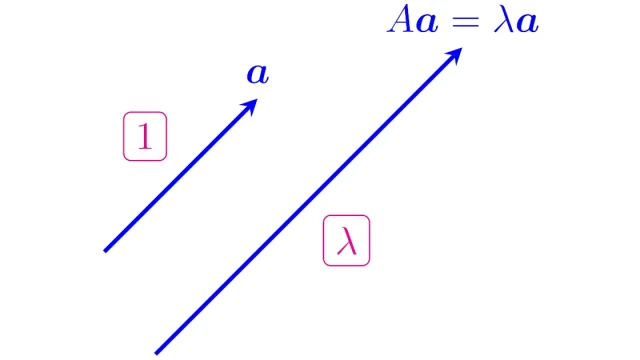
正方行列Aの固有値は固有方程式|tI-A|=0を解くことで求めることができ,Aの固有値λに属する固有ベクトルは固有値・固有ベクトルの定義から得られる連立1方程式を解くことで得られます.
 線形代数学の基本
線形代数学の基本 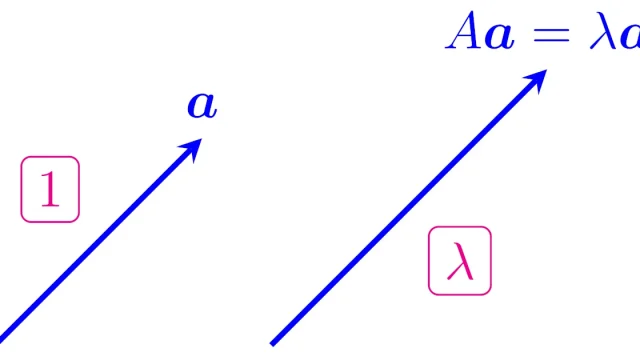 線形代数学の基本
線形代数学の基本  線形代数学の基本
線形代数学の基本  線形代数学の基本
線形代数学の基本  線形代数学の基本
線形代数学の基本  線形代数学の基本
線形代数学の基本  線形代数学の基本
線形代数学の基本  線形代数学の基本
線形代数学の基本  線形代数学の基本
線形代数学の基本  線形代数学の基本
線形代数学の基本