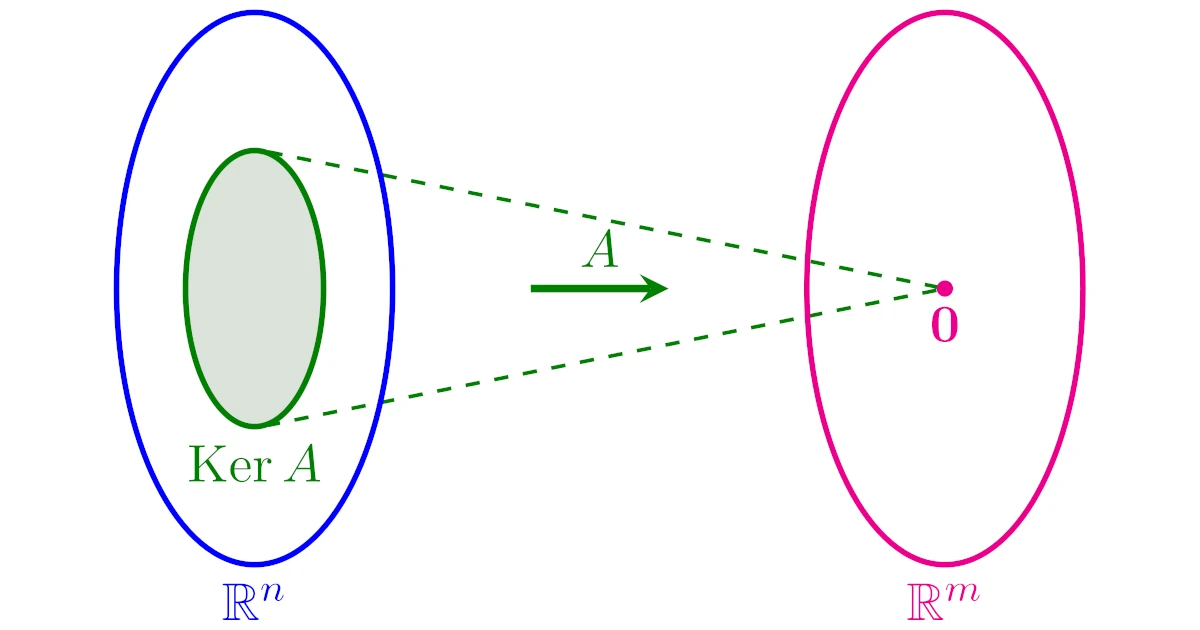
$\R^n$の部分空間である行列の像に並んで大切な部分空間に行列の核と呼ばれるものがあります.
例えば,行列$A$を$A=\bmat{1&2&2\\1&1&0}$とするとき,
\begin{align*}A\bmat{1\\1\\0}=\bmat{3\\2},\quad
A\bmat{2\\-2\\1}=\bmat{0\\0}\end{align*}
のように,3次列ベクトルに$A$を左からかけると2次列ベクトルができあがりますね.
いま列ベクトル$\bmat{2\\-2\\1}$に左から行列$A$をかけると零ベクトル$\bmat{0\\0}$になりましたが,このように左から行列$A$をかけて零ベクトルになる列ベクトルたちを全て集めてできる集合を$A$の核といいます.
この記事では
- 行列の核の定義
- 行列の核の具体例
- 行列の核が部分空間であることの証明
を順に説明します.
なお,特に断らない限り以下では実行列・実ベクトルを扱うことにしますが,複素行列など一般の体を成分とする行列・ベクトルに対しても同様です.
この記事の内容は一般の線形写像でも同様に成り立ちますが,簡単のためここでは$\R^n$の部分空間に限って話を進めます.
「線形代数学の基本」の一連の記事
- 行列と列ベクトル
- 行列式
- $\R^n$の部分空間と基底
行列の核の定義
$m\times n$行列$A$を考える.$A$を左からかけて零ベクトル$\m{0}_m$となる$\R^n$の列ベクトル全部からなる集合を$A$の核(kernel)といい,$\Ker{A}$と表す:
\begin{align*}\Ker{A}=\set{\m{x}\in\R^n}{A\m{x}=\m{0}_m}.\end{align*}
核の定義の$A\m{x}=\m{0}_m$は連立1次方程式なので,行列$A$の核$\Ker{A}$は$A\m{x}=\m{0}_m$の解全部の集合と言っても同じことですね.
このため,核$\Ker{A}$は$A\m{x}=\m{0}_m$の解空間と呼ばれることもよくあります.
冒頭の行列$A=\bmat{1&2&2\\1&1&0}$に対しては,例えば
\begin{align*}A\bmat{2\\-2\\1}=\bmat{0\\0}\end{align*}
が成り立ちましたから,$\bmat{2\\-2\\1}\in\Ker{A}$というわけですね.
核$\Ker{A}$は「行列$A$をかける前の空間」の話であるという点をしっかり意識しましょう.
行列の像$\Ima{A}$は「行列$A$をかけた後の空間」の話でした.今回の行列の核とは考えている空間が異なる点に注意してください.
行列の核の具体例
具体的に行列の核を求めてみましょう.
例1
冒頭で考えた行列$A$の像を考えましょう.
$A=\bmat{2&3&-1\\1&1&1}$とする.$\Ker{A}$を求めよ.
繰り返しになりますが,行列$A$は3次列ベクトルに左からかけることができ,このとき2次列ベクトルができあがりますね.
核$\Ker{A}$は連立1次方程式$A\m{x}=\m{0}$の解を全部集めたものなので,$A\m{x}=\m{0}$を解けばいいですね.
行基本変形により
\begin{align*}A\to\bmat{0&1&-3\\1&1&1}\to\bmat{0&1&-3\\1&0&4}\end{align*}
と簡約化される.この簡約化の第3列に主成分が存在しないから,掃き出し法の考え方より第3成分に任意定数を与えて,連立1次方程式$A\m{x}=\m{0}$の解
\begin{align*}\m{x}=\bmat{-4t\\3t\\t}=t\bmat{-4\\3\\1}\quad (t\in\R)\end{align*}
を得る.よって,定義より
\begin{align*}\Ker{A}=&\set{\m{x}\in\R^3}{A\m{x}=\m{0}}
\\=&\set{t\bmat{-4\\3\\1}}{t\in\R}
\\=&\spn{\bra{\bmat{-4\\3\\1}}}\end{align*}
である.
いま求まった生成される空間$\spn{\bra{\bmat{-4\\3\\1}}}$は$\R^3$の部分空間ですね.
例2
$A=\bmat{1&2&-1&1\\2&4&-1&3\\-1&-2&3&1}$とする.$\Ker{A}$を求めよ.
今回の行列$A$は4次列ベクトルに左からかけることができ,このとき3次列ベクトルができあがりますね.
やはり核$\Ker{A}$は連立1次方程式$A\m{x}=\m{0}$の解を全部集めたものなので,$A\m{x}=\m{0}$を解けばいいですね.
行基本変形により
\begin{align*}A\to\bmat{1&2&-1&1\\0&0&1&1\\0&0&2&2}\to\bmat{1&2&0&2\\0&0&1&1\\0&0&0&0}\end{align*}
と簡約化される.この簡約化の第2列・第4列に主成分が存在しないから,掃き出し法の考え方より第2成分・第4成分に任意定数を与えて,連立1次方程式$A\m{x}=\m{0}$の解
\begin{align*}\m{x}=\bmat{-2s-2t\\s\\-t\\t}=s\bmat{-2\\1\\0\\0}+t\bmat{-2\\0\\-1\\1} (s,t\in\R)\end{align*}
を得る.よって,定義より
\begin{align*}\Ker{A}=&\set{\m{x}\in\R^4}{A\m{x}=\m{0}}
\\=&\set{s\bmat{-2\\1\\0\\0}+t\bmat{-2\\0\\-1\\1}}{s,t\in\R}
\\=&\spn{\bra{\bmat{-2\\1\\0\\0},\bmat{-2\\0\\-1\\1}}}\end{align*}
である.
いま求まった生成される空間$\spn{\bra{\bmat{-2\\1\\0\\0},\bmat{-2\\0\\-1\\1}}}$は$\R^4$の部分空間ですね.
部分空間としての行列の核
いまの例からみてとれるように,行列の核は部分空間となります.
行列の核が部分空間になることの証明
$m\times n$行列$A$に対して,$\Ker{A}$は$\R^n$の部分空間である.
$A\m{0}_n=\m{0}_m$だから,$\Ker{A}\neq\emptyset$である.
[1] 和について閉じていることを示す.任意に$\m{a},\m{b}\in\Ker{A}$をとる.
このとき,$A\m{a}=\m{0}$, $A\m{b}=\m{0}$だから
\begin{align*}A(\m{a}+\m{b})=A\m{a}+A\m{b}=\m{0}+\m{0}=\m{0}\end{align*}
が成り立つ.
[2] スカラー倍について閉じていることを示す.任意に$\m{a}\in\Ker{A}$, $k\in\R$をとる.
このとき,$A\m{a}=\m{0}$だから
\begin{align*}A(k\m{a})=k(A\m{a})=k\m{0}=\m{0}\end{align*}
が成り立つ.よって,$k\m{a}\in\Ker{A}$が成り立つ.
[1], [2]より$\Ker{A}$は和・スカラー倍について閉じているから,$\R^n$の部分空間である.
行列の核の次元
$m\times n$行列$A$に対して,連立1次方程式$A\m{x}=\m{0}$の解の自由度(解が持つ任意定数の個数)が$n-\rank{A}$であることを思い出すと,上の例の考え方と併せて次が成り立ちます.
$m\times n$行列$A$に対して,$\dim{\Ker{A}}=n-\rank{A}$が成り立つ.
$A$のランクを$r=\rank{A}$とすると,$\m{x}\in\R^n$の方程式$A\m{x}=\m{0}_m$の解の自由度は$n-r$である.
これより,ある線形独立な$\m{b}_1,\m{b}_2,\dots,\m{b}_{n-r}\in\R^n$が存在して,解は
\begin{align*}\m{x}=t_1\m{b}_1+t_2\m{b}_2+\dots+t_{n-r}\m{b}_{n-r}\end{align*}
と任意定数$t_1,t_2,\dots,t_{n-r}$を用いて表すことができる.よって,
\begin{align*}\Ker{A}=\spn{(\m{b}_1,\m{b}_2,\dots,\m{b}_{n-r})}\end{align*}
が成り立つ.$\m{b}_1,\m{b}_2,\dots,\m{b}_{n-r}$の線形独立性と併せて$\dim{\Ker{A}}=n-\rank{A}$が成り立つ.
次元定理
行列$A$の像$\Ima{A}$の次元が$\dim{\Ima{A}}=\rank{A}$であることを思い出すと,上で示した定理と併せて次の系が成り立ちますね.
$m\times n$行列$A$に対して,$\dim{\Ima{A}}+\dim{\Ker{A}}=n$が成り立つ.
$m\times n$行列$A$について$\dim{\Ker{A}}=n-\rank{A}$と$\dim{\Ima{A}}=\rank{A}$が成り立つから,辺々足し合わせて$\dim{\Ima{A}}+\dim{\Ker{A}}=n$を得る.
この系は一般に次元定理と呼ばれています.



コメント