これまでの記事で$\R^n$の部分空間について扱ってきました.
$\R^n$の部分空間は和とスカラー倍について閉じている「集合」でしたから,部分空間が複数あるときにはそれらの共通部分を考えることもあります.
実は$\R^n$の部分空間の共通部分も$\R^n$の部分空間になり,基底や次元を考えることはよくあります.
この記事では,$\R^n$の部分空間として
- 部分空間の共通部分の定義
- 共通部分の基底と次元の具体例
を順に説明します.
なお,特に断らない限り以下では実行列・実ベクトルを扱うことにしますが,複素行列など一般の体を成分とする行列・ベクトルに対しても同様です.
この記事の内容は一般の線形空間でも同様に成り立ちますが,簡単のためここでは$\R^n$の部分空間に限って話を進めます.
「線形代数学の基本」の一連の記事
- 行列と列ベクトル
- 行列式
- $\R^n$の部分空間と基底
部分空間の共通部分
一般に(部分空間とは限らない)2つの集合$A,B$の共通部分とは,平たくいえば$A$にも$B$にも属する元を全て集めてできる集合のことをいうのでした.
集合$X$の部分集合$A,B$に対して,集合
$A\cap B=\set{x\in X}{x\in A\ \text{かつ}\ x\in B}$
を$A,B$の共通部分(intersection)といい$A\cap B$と表す.
$\R^n$の部分空間の集合としての共通部分は,次のように$\R^n$の部分空間となります.
$\R^n$の部分空間$U,V$に対して,共通部分
$U\cap V=\set{\m{a}\in\R^n}{\m{a}\in U\ \text{かつ}\ \m{a}\in V}$
は$\R^n$の部分空間となる.
$U,V$は$\R^n$の部分空間で,$\R^n$の任意の部分空間は零ベクトル$\m{0}_n$を元にもつから,$\m{0}_n\in U$かつ$\m{0}_n\in V$が成り立つ.よって,$\m{0}_n\in U\cap V$だから,$U\cap V$は空でない.
[1] 和について閉じていることを示す.任意に$\m{a},\m{b}\in U\cap V$をとる.
このとき,$\m{a},\m{b}\in U$であり,$U$は$\R^n$の部分空間だから$\m{a}+\m{b}\in U$が成り立つ.
同様に$\m{a}+\m{b}\in V$も成り立つから,$\m{a}+\m{b}\in U\cap V$が成り立つ.
[2] スカラー倍について閉じていることを示す.任意に$\m{b}\in U\cap V$, $k\in\R$をとる.
このとき,$\m{a}\in U$であり,$U$は$\R^n$の部分空間だから$k\m{a}\in U$が成り立つ.
同様に$k\m{a}\in V$も成り立つから,$k\m{a}\in U\cap V$が成り立つ.
[1], [2]より$U\cap V$は和とスカラー倍について閉じているから,$\R^n$の部分空間である.
この記事では2つの部分空間の共通部分のみ扱いますが,3つ以上の部分空間の共通部分についても帰納的に部分空間となります.
具体例
いくつか具体例を考えましょう.
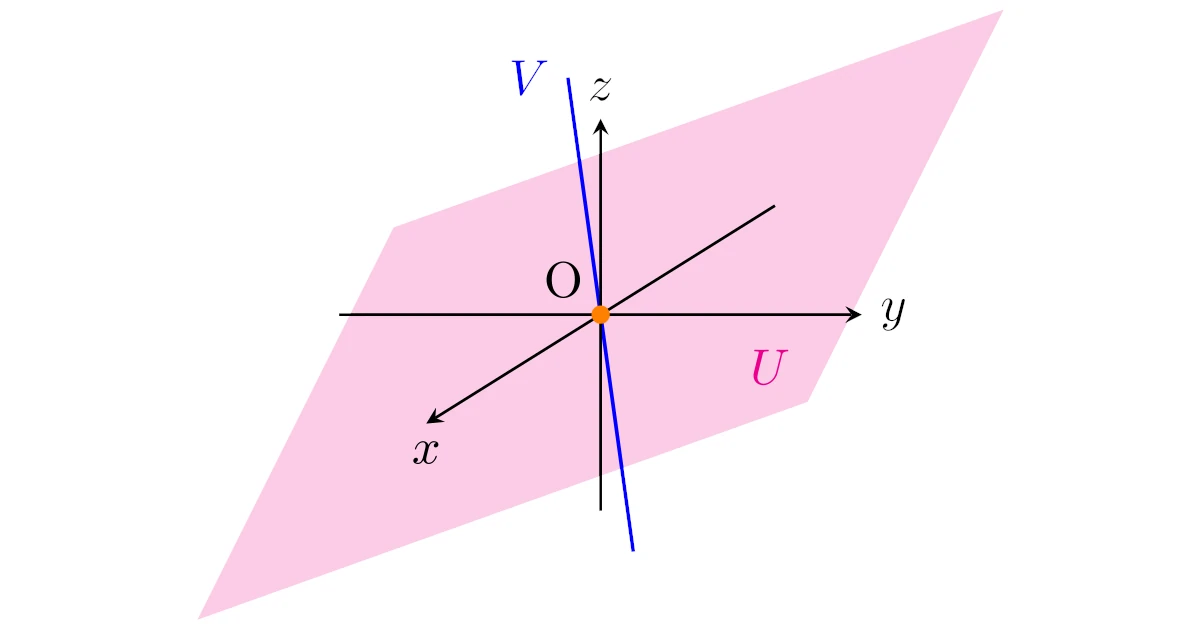
例1(平面と平面の共通部分1)
$\R^3$の部分空間$U,V$を
\begin{align*}U=\set{\bmat{x\\y\\z}\in\R^3}{z=0},\quad
V=\set{\bmat{x\\y\\z}\in\R^3}{x=0}\end{align*}
とするとき,共通部分$U\cap V$の基底が存在すれば1組求め,次元$\dim{(U\cap V)}$を求めよ.
$U$は$xy$平面,$V$は$yz$平面ですから,これらの共通部分$U\cap V$は$y$軸となりますね.
共通部分$U\cap V$は
\begin{align*}U\cap V=&\set{\bmat{x\\y\\z}\in\R^3}{x=0,z=0}
\\=&\set{y\bmat{0\\1\\0}}{y\in\R}=\spn{\bra{\bmat{0\\1\\0}}}\end{align*}
である.
また,一般にひとつだけのベクトルは線形独立なので$\bmat{0\\1\\0}$は線形独立だから,$\anb{\bmat{0\\1\\0}}$は共通部分$U\cap V$の基底であり,$\dim{(U\cap V)}=1$である.
例2(平面と平面の共通部分2)
$\R^3$の部分空間$U,V$を
\begin{align*}U=&\set{\bmat{x\\y\\z}\in\R^3}{x+2y-z=0},
\\V=&\set{\bmat{x\\y\\z}\in\R^3}{2x+y+z=0}\end{align*}
とするとき,共通部分$U\cap V$の基底が存在すれば1組求め,次元$\dim{(U\cap V)}$を求めよ.
今回の$U,V$も$\R^3$上の平面で平行でないので,これらの共通部分はこれらの交線となり共通部分$U\cap V$は1次元の部分空間となります.
共通部分$U\cap V$は
\begin{align*}U\cap V=&\set{\bmat{x\\y\\z}\in\R^3}{\begin{gathered}x+2y-z=0,\\2x+y+z=0\end{gathered}}\end{align*}
である.ここで,条件の斉次連立1次方程式
\begin{align*}\begin{cases}x+2y-z=0,\\2x+y+z=0\end{cases}\end{align*}
\begin{align*}\bmat{1&2&-1\\2&1&1}\to\bmat{1&2&-1\\0&-3&3}\to\bmat{1&0&1\\0&-1&1}\end{align*}
と簡約化できるから,主成分が存在しない第3列に対応する未知数$z$に任意定数$k$を与えて$(x,y,z)=(-k,k,k)$と解ける.よって,
\begin{align*}U\cap V=&\set{\bmat{-k\\k\\k}}{k\in\R}
\\=&\set{k\bmat{-1\\1\\1}}{k\in\R}=\spn{\bra{\bmat{-1\\1\\1}}}\end{align*}
である.
また,一般にひとつだけのベクトルは線形独立なので$\bmat{-1\\1\\1}$は線形独立だから,$\anb{\bmat{-1\\1\\1}}$は共通部分$U\cap V$の基底であり,$\dim{(U\cap V)}=1$である.
例3(平面と直線の共通部分1)
$\R^3$の部分空間$U,V$を
\begin{align*}U=&\set{\bmat{x\\y\\z}\in\R^3}{x+2y-z=0},
\\V=&\set{\bmat{x\\y\\z}\in\R^3}{\begin{aligned}&x+y+z=0,\\&x-y=0\end{aligned}}\end{align*}
とするとき,共通部分$U\cap V$の基底が存在すれば1組求め,次元$\dim{(U\cap V)}$を求めよ.
今回は$U$が平面で$V$は直線ですね.直線$V$は平面$U$にブスッと突き刺さっているので,$U\cap V$は零ベクトル$\m{0}_3$のみの集合となります.
共通部分$U\cap V$は
\begin{align*}U\cap V=&\set{\bmat{x\\y\\z}\in\R^3}{\begin{gathered}x+2y-z=0,\\x+y+z=0\\x-y=0\end{gathered}}\end{align*}
である.ここで,条件の斉次連立1次方程式
\begin{align*}\begin{cases}x+2y-z=0,\\x+y+z=0,\\x-y=0\end{cases}\end{align*}
\begin{align*}\bmat{1&2&-1\\1&1&1\\1&-1&0}\to\bmat{1&2&-1\\0&-1&2\\0&-3&1}\to\bmat{1&0&0\\0&1&0\\0&0&1}\end{align*}
と簡約化できるから,解は自明解$(x,y,z)=(0,0,0)$に限る.よって,$U\cap V=\{\m{0}_3\}$なので,$U\cap V$は基底を持たず$\dim{(U\cap V)}=0$である.
零ベクトルのみからなる部分空間はいつでも部分空間となるので,自明な部分空間というのでした.
例4(平面と直線の共通部分2)
$\R^3$の部分空間$U,V$を
\begin{align*}U=&\set{\bmat{x\\y\\z}\in\R^3}{3x+z=0},
\\V=&\set{\bmat{x\\y\\z}\in\R^3}{\begin{aligned}&2x+y+z=0,\\&x-y=0\end{aligned}}\end{align*}
例3と同じく$U$が平面で$V$は直線ですが,今回は平面$U$上に直線$V$が「乗って」いるので,$U\cap V$は1次元の部分空間となります.
共通部分$U\cap V$は
\begin{align*}U\cap V=&\set{\bmat{x\\y\\z}\in\R^3}{\begin{gathered}3x+z=0,\\2x+y+z=0\\x-y=0\end{gathered}}\end{align*}
である.ここで,条件の斉次連立1次方程式
\begin{align*}\begin{cases}3x+z=0,\\2x+y+z=0\\x-y=0\end{cases}\end{align*}
\begin{align*}\bmat{3&0&1\\2&1&1\\1&-1&0}\to\bmat{0&3&1\\0&3&1\\1&-1&0}\to\bmat{1&-1&0\\0&3&1\\0&0&0}\end{align*}
と簡約化できるから,任意定数$k$を用いて$(x,y,z)=(k,k,-3k)$と解ける.よって,
\begin{align*}U\cap V=&\set{\bmat{k\\k\\-3k}}{k\in\R}
\\=&\set{k\bmat{1\\1\\-3}}{k\in\R}=\spn{\bra{\bmat{1\\1\\-3}}}\end{align*}
である.また,一般にひとつだけのベクトルは線形独立なので$\bmat{1\\1\\-3}$は線形独立だから,$\anb{\bmat{1\\1\\-3}}$は共通部分$U\cap V$の基底であり,$\dim{(U\cap V)}=1$である.
例5(空間と空間の共通部分)
$\R^4$の部分空間$U,V$を
\begin{align*}U=&\set{\bmat{x\\y\\z\\w}\in\R^4}{x+2y-z+w=0},
\\V=&\set{\bmat{x\\y\\z\\w}\in\R^4}{x+2y-w=0}\end{align*}
もとが4次元で$U$も$V$も3次元空間なので図を描くのは難しいですが,考え方はこれまでの例と同じです.
共通部分$U\cap V$は
\begin{align*}U\cap V=&\set{\bmat{x\\y\\z}\in\R^3}{\begin{gathered}x+2y-z+w=0,\\x+2y-w=0\end{gathered}}\end{align*}
である.ここで,条件の斉次連立1次方程式
\begin{align*}\begin{cases}x+2y-z+w=0,\\x+2y-w=0\end{cases}\end{align*}
\begin{align*}\bmat{1&2&-1&1\\1&2&0&-1}\to\bmat{1&2&-1&1\\0&0&1&-2}\to\bmat{1&2&0&-1\\0&0&1&-2}\end{align*}
と簡約化できるから,任意定数$k,\ell$を用いて$(x,y,z,w)=(-2k+\ell,k,2\ell,\ell)$と解ける.よって,
\begin{align*}U\cap V=&\set{\bmat{-2k+\ell\\k\\2\ell\\\ell}}{k,\ell\in\R}
\\=&\set{k\bmat{-2\\1\\0\\0}+\ell\bmat{1\\0\\2\\1}}{k,\ell\in\R}=\spn{\bra{\bmat{-2\\1\\0\\0},\bmat{1\\0\\2\\1}}}\end{align*}
である.また,一般に2つのベクトルが平行でなければ線形独立なので$\bmat{-2\\1\\0\\0},\bmat{1\\0\\2\\1}$は線形独立だから,$\anb{\bmat{-2\\1\\0\\0},\bmat{1\\0\\2\\1}}$は共通部分$U\cap V$の基底であり,$\dim{(U\cap V)}=2$である.



コメント