連結の定義と具体例｜位相空間上の「ひとまとまりな集合」

位相空間$X$において「集合$A\subset X$がひとまとまりになっていること」を表す概念として連結性があります．

大雑把に言えば「集合$A$が２つの開集合によって分けられない」とき，集合$A$は連結であるといいます．

似た概念に弧状連結性がありますが，実は「弧状連結なら連結」は成り立ちますが逆は成り立ちません．つまり，連結性の方が少し広い性質となっています．

この記事では

連結性の定義と具体例
連結性と弧状連結性の関係
参考文献

を順に解説します．

なお，この記事では$X$を位相空間とします．

位相空間をよく知らない方は$X$をユークリッド空間$\R$, $\R^2$（数直線，$xy$平面）と思って読み進めても内容は理解できます．

「連結性」の一連の記事

連結性の定義と具体例
連結性と弧状連結性の関係
1. 連結な集合の連続写像による像も連結
2. 連結性は弧状連結より広い概念
参考文献
1. 集合・位相入門
2. 集合と位相

連結性の定義と具体例

連結性を定義して具体例を考えましょう．

２つの開集合で分けられない集合を連結という

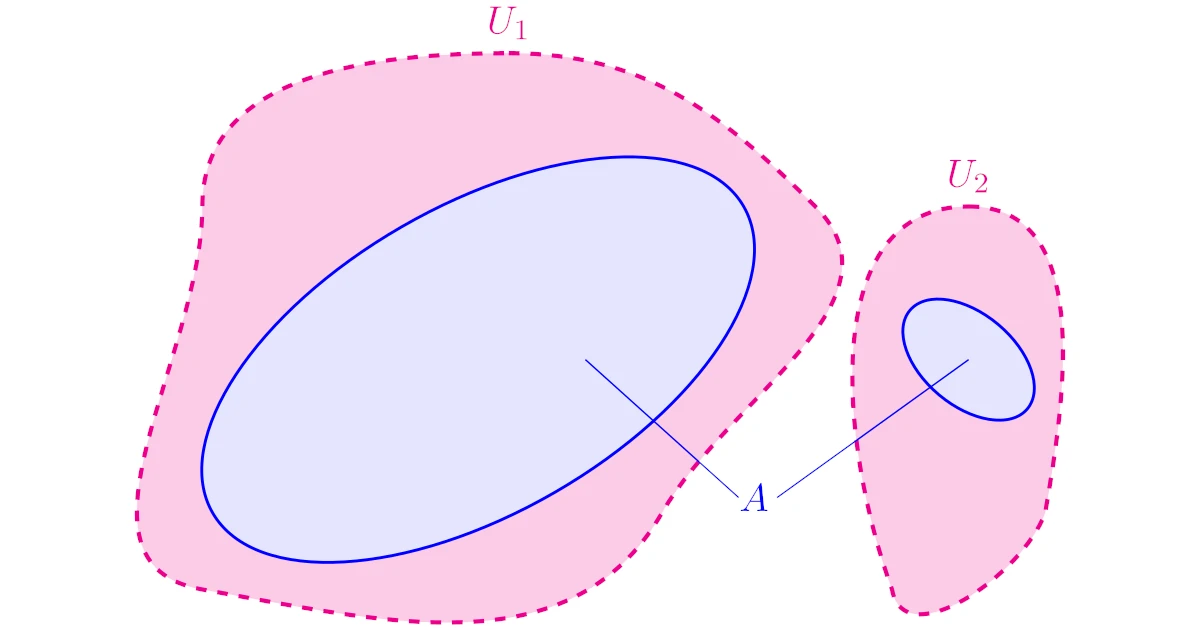
集合$A\subset X$が連結であるとは，３つの条件

$A\subset U_1\cup U_2$
$U_1\cap U_2=\emptyset$
$A\cap U_{i}\neq\emptyset$（$i=1,2$）

を満たす$X$上の開集合$U_1$, $U_2$が存在しないことをいう．

３つの条件を満たす$X$上の開集合$U_1$, $U_2$が存在するときは非連結であるという．

もし「離れ小島」があれば，異なる「島」は２つの開集合で分けられますから，集合$A$は「ひとまとまり」とは言えないというイメージですね．

$定義の条件を満たす集合A,U₁,U₂$

集合$A$は２つの空でない開集合$U_1$と$U_2$で分けられているので連結でない

このような２つの開集合$U_1$, $U_2$が存在しないとき，集合$A$は連結であるというわけですね．

連結開集合を領域という

数学ではよく領域という言葉が使われますが，これは次のように定義されます．

集合$A\subset X$が領域であるとは，$A$が連結な開集合であることをいう．

高校数学では「軌跡と領域」の分野で「ベタッと塗りつぶせるような集合」をざっくり領域と呼ぶことが多かったと思いますが，大学以降の数学で領域というとこの定義の通り連結な開集合のことを指すことが多いです．

大学以降の数学でも誤解が生じないときは深く考えず「ベタッと塗りつぶせるような集合」を領域と呼ぶこともなくはありませんが，話し手も聞き手も注意が必要です．

具体例１（連結な集合）

集合$[0,1]\subset\R$は連結であることを示せ．ただし，$\R$は１次元ユークリッド空間（通常の数直線）とする．

$０以上１以下の区間I$

区間$[0,1]$に対して，定義の条件を満たす$U_1$, $U_2$が取れないことを示せばよい

背理法により示す．すなわち，$I:=[0,1]$が連結でないと仮定して矛盾を導く．$I:=[0,1]$が連結でないなら，

\begin{align*}&I\subset U_1\cup U_2,\quad
U_1\cap U_2=\emptyset,
\\&I\cap U_i\neq\emptyset\quad (i=1,2)\end{align*}

を満たす$\R$上の開集合$U_1$, $U_2$が存在する．

$U_1$, $U_2$は対称なので$1\in U_2$としてよく，このときある$\epsilon>0$が存在して$(1-\epsilon,1]\subset U_2$が成り立つ．$a:=\sup{(I\cap U_1)}$とおくと，$U_1\cap U_2=\emptyset$と併せて$a\le1-\epsilon<1$である．

$区間Iと開集合V₁$

$1\in U_2$だから，1のある近傍と$U_1$は共通部分をもたない

$U_1$は開集合だから$a\not\in U_1$であり，$I\subset U_1\cup U_2$と併せると$a\in U_2$である．

$U_2$は開集合だから$a$のある近傍$U$が存在して$U\subset U_2$となるが，$a=\sup{(I\cap U_1)}$より$U\cap U_1\neq\emptyset$となって$U_1\cap U_2=\emptyset$に矛盾する．

一般に$\R$上の任意の区間は連結となります．

このことから，$\R$上の区間を$\R$の連結部分集合と定義することもあります．

具体例２（連結でない集合）

$\R^2$を２次元ユークリッド空間（通常の$xy$平面）とする．$A\subset\R^2$を

\begin{align*}A=\set{\bmat{x\\0}\in\R^2}{x\neq0}\end{align*}

とすると，$A$が連結でないことを示せ．

$x軸上の第1成分が正の部分と負の部分の和集合A$

集合$A$は原点で分かれているので，これを利用して2つの空でない開集合で分ければよい

$A$は$x$軸から原点を除いた集合ですね．

$U_i\subset\R^2$（$i=1,2$）を

\begin{align*}U_1=\set{\bmat{x\\y}\in\R^2}{x>0},\quad
U_2=\set{\bmat{x\\y}\in\R^2}{x<0}\end{align*}

で定める．

$集合Aと開集合U₁,U₂$

2つの開集合$U_1$, $U_2$により$A$が分けられる

このとき，

\begin{align*}&A\subset U_1\cup U_2,\quad
U_1\cap U_2=\emptyset,
\\&A\cap U_i\neq\emptyset\quad (i=1,2)\end{align*}

を満たすので，$A$は連結でない．

連結性と弧状連結性の関係

連結性の基本的な性質をいくつか解説します．

連結な集合の連続写像による像も連結

直観的には，連続写像は集合の「つながり方」を保存するので，連結性も保存しそうですね．

$X$, $Y$を位相空間とし，$f:X\to Y$を連続写像とし，$A\subset X$とする．$A$が$X$上で連結なら，$f(A)$は$Y$上で連結である．

対偶を示す．$f(A)$は$Y$上で連結でないと仮定する．このとき，

\begin{align*}&f(A)\subset U_1\cup U_2,\quad
U_1\cap U_2=\emptyset,
\\&f(A)\cap U_i\neq\emptyset\quad (i=1,2)\end{align*}

なる$Y$上の開集合$U_1,U_2$が存在する．このとき，$V_i:=f^{-1}(U_i)$を定めると，$f$の連続性より$V_i$は開集合であり（$i=1,2$），

$A\subset f^{-1}(f(A))\subset f^{-1}(U_1\cup U_2)=V_1\cup V_2$
$V_1\cap V_2=f^{-1}(U_1\cap U_2)=f^{-1}(\emptyset)=\emptyset$
$b\in f(A)\cap U_i$をとると，ある$a\in A$が存在して$f(a)=b\in U_i$だから$a\in V_i$が得られ，$A\cap V_i\neq\emptyset$

が成り立つ．よって，$A$は連結でないことが分かり，これで対偶が示された．

$A\subset f^{-1}(f(A))$であり，等号が成り立つとは限らないことに注意してください．