ユークリッド空間$\R^n$などの距離空間上の写像の連続性は$\epsilon\text{-}\delta$論法を用いて定義するのが普通です．
この$\epsilon\text{-}\delta$論法による写像の連続性の定義は距離を用いた定義なので，一般に距離が定まっているとは限らない位相空間上では同じように写像の連続性を定義することはできません．
そこで距離空間での連続性の定義を距離を用いない条件に言い換えることができれば，その条件を位相空間上の写像の連続性を定義とすることができそうですね．
そこで，この記事では
- 距離空間上の写像の連続性の定義
- 位相空間の定義
- 距離空間の位相
- 位相空間上の写像の連続性の定義
を順に説明します．
距離空間上の連続写像
まずは距離空間上の連続写像の定義を確認しておきましょう．
ユークリッド空間の連続性
一般の距離空間上の連続写像の話に移る前に，ユークリッド空間$\R^n$上の関数の連続性の定義を確認しておきます．
[写像$\R^n\to\R^m$の連続性] $\Omega\subset\R^n$とする．関数$f:\Omega\to\R^m$が点$a\in\Omega$で連続 (continuity)であるとは，任意の$\epsilon>0$に対して，ある$\delta>0$が存在して，
また，$f$が集合$\Omega’\subset\Omega$上で連続であるとは，集合$\Omega’$上の任意の点で$f$が連続であることをいう．
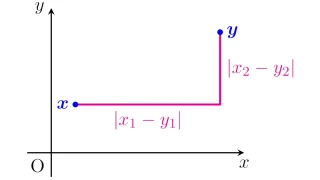
ただし，$x=(x_1,\dots,x_n)\in\R^{n}$に対して，$|x|=\sqrt{{x_1}^2+\dots+{x_n}^2}$である．
この定義[写像$\R^n\to\R^m$の連続性]の点$a\in\Omega$での連続性の定義の方法を[$\epsilon\text{-}\delta$論法]と言いますね．
この定義は距離空間の連続写像の特別な場合に過ぎませんが，連続写像$\R^n\to\R^m$のイメージをもっていると距離空間上の写像の連続性の定義を理解する助けになります．
距離空間の定義
次に距離空間の定義を確認します．
[距離空間] 集合$X$と写像$d:X\times X\to \R$の組$(X,d)$が距離空間 (metric space)であるとは，写像$d$が次の３条件を同時に満たすことをいう．
- $d(x,y)=0$であることと，$x=y$であることは同値である(非退化性)．
- 任意の$x,y\in X$に対して$d(x,y)=d(y,x)$を満たす(対称性)．
- 任意の$x,y,z\in X$に対して$d(x,z)\le d(x,y)+d(y,z)$を満たす(劣加法性)．
が成り立つことをいう．
このとき，写像$d$を距離空間$(X,d)$の距離 (distance)という．距離空間$(X,d)$を単に$X$と書くこともある．
距離の定義に次の非負値性を含めることもありますが，非負値性は上の定義の３性質から導くことができます．
[距離の非負値性] 距離空間$(X,d)$に対して，任意の$x,y\in X$は$d(x,y)\ge0$を満たす．
この[距離の非負値性]の証明や距離空間の定義のイメージについては，以下の記事を参照してください．
距離空間の連続写像
通常，距離空間上の連続写像は次のように定義されます．
[距離空間上の連続写像] $(X,d_1)$, $(Y,d_2)$を距離空間とする．写像$f:X\to Y$が点$a\in X$で連続であるとは，任意の$\epsilon>0$に対して，ある$\delta>0$が存在して，$d_1(x,a)<\delta$なら
が成り立つことをいう．
また，$f$が$X$上で連続であるとは$X$上の任意の点で$f$が連続であることをいう．
具体的に距離空間$(X,d_1)$, $(Y,d_2)$を
- $X=\R^n$, $d_1:\R^n\times\R^n\to\R;(x,y)\mapsto|x-y|$
- $Y=\R^m$, $d_2:\R^m\times\R^m\to\R;(x,y)\mapsto|x-y|$
で定めると，最初に確認した定義[写像$\R^n\to\R^m$の連続性]になりますね．
位相空間と距離空間
次に距離空間を自然に位相空間とみなすことができることを説明します
位相空間の定義
まずは位相空間の定義を確認しておきましょう．
[位相空間] 集合$X$と，$X$の部分集合族(部分集合の集合)$\mathcal{O}$の組$(X,\mathcal{O})$が位相空間 (topological space)であるとは，次の1-3を満たすことをいう．
- 空集合$\emptyset$と全体集合$X$はともに$\mathcal{O}$に属する：$\emptyset,X\in\mathcal{O}$
- $\mathcal{O}$の有限個の元$O_1,\dots,O_n$の共通部分$\bigcap\limits_{i=1}^{n}O_i$も$\mathcal{O}$に属する：$\bigcap\limits_{i=1}^{n}O_i\in\mathcal{O}$
- $\mathcal{O}$の任意個(無限個も可)の元$O_{\lambda}$ $(\lambda\in\Lambda)$の和集合$\bigcup\limits_{\lambda\in\Lambda}O_{\lambda}$も$\mathcal{O}$に属する：$\bigcup\limits_{\lambda\in\Lambda}O_{\lambda}\in\mathcal{O}$
このとき，部分集合族$\mathcal{O}$は集合$X$の開集合系 (open sets)であるという．また，位相空間$(X,\mathcal{O})$を単に$X$と書くこともある．
なお，$\mathcal{O}$の任意個(無限個も可)の元を$O_n$ $(n=1,2,\dots)$ではなく$O_{\lambda}$ $(\lambda\in\Lambda)$とするのは，この「任意個」が「可算個」ではないかもしれないからです．可算でなければ並べられないので$O_n$ $(n=1,2,\dots)$と表すことができません．
本来，位相とは開集合系を定めることによって定まる数学的構造のことを指しますが，簡単に開集合系$\mathcal{O}$を指して位相ということも多いです．
距離空間の位相
ここで距離空間の開近傍の定義を確認しておきましょう．
距離空間$(X,d)$を考える．$a\in X$, $r>0$に対し，集合
を点$a$の$r$開近傍 (open neighborhood)という．
開近傍は単に近傍と呼ばれることも多いですね．
次の命題は距離空間と位相空間を繋ぐ重要な役割を果たします．
[距離空間の位相] 距離空間$X$は次の性質$(*)$をみたす$X$の部分集合$O$全部の族$\mathcal{O}$を開集合系として位相空間になる．
$(*)$：$a\in O$なら，ある$r>0$が存在して$U_{r}(a)\subset O$をみたす．
位相空間の定義の(1)～(3)を確認すれば良い．
[(1)の証明] $U=\emptyset,X$は明らかに$(*)$をみたすから，$\emptyset$, $X\in\mathcal{O}$が従う($U=\emptyset$に対しては，$a\in U$が偽なので，$(*)$が真となることに注意)．
[(2)の証明] $\mathcal{O}$の有限個の元$O_1,\dots,O_n$をとり，$a\in\bigcap\limits_{i=1}^{n}O_i$であるとすると，各$i\in{1,\dots,n}$に対して，$U_{r_i}(a) \subset O_i$をみたす$r_i>0$が存在する．
よって，$r:=\min{\{r_1,\dots,r_n\}}$とすれば，$U_{r}(a)\in\bigcap\limits_{i=1}^{n}O_i$をみたすから，$\bigcap\limits_{i=1}^{n}O_i\in\mathcal{O}$が従う．
[(3)の証明] $\mathcal{O}$の任意個(無限個も可)の元$O_{\lambda}$ $(\lambda\in\Lambda)$をとり，$a\in\bigcup\limits_{\lambda\in\Lambda}O_{\lambda}$であるとすると，$a\in O_{\lambda}$をみたす$\lambda\in\Lambda$が存在する．
このとき，$U_{r}(a)\subset O_\lambda$をみたす$r>0$が存在する．
もとより，$O_\lambda\subset\bigcup\limits_{\lambda\in\Lambda}O_{\lambda}$だから，$\bigcup\limits_{\lambda\in\Lambda}O_{\lambda}\in\mathcal{O}$が従う．
学部１年生ではユークリッド空間$\R^{n}$上の開集合の定義を$(*)$の形で学び，学部２年生の位相空間の授業で位相空間の開集合の定義を学ぶ際に
「１年生で学んだユークリッド$\R^{n}$上の開集合は性質$(*)$をみたす．よって，ユークリッド空間$\R^{n}$は位相空間となる．」
と学ぶことが学ぶことが多いですね．
以降，この命題[距離空間の位相]により定まる位相を距離空間の位相とします．
位相空間上の連続写像
それでは一般の位相空間上の連続写像を定義しましょう．
距離空間の開集合と連続写像
一般の位相空間には距離が定義されていないため，$\epsilon\text{-}\delta$論法で位相空間の連続性を定義することはできません．
また，距離空間は位相空間の一種なので距離空間上の写像の連続性に矛盾しないように定めなければなりません．そこで，次の定理がポイントとなります．
[連続写像の同値条件] ２つの距離空間$(X,d_1)$, $(Y,d_2)$と写像$f:X\to Y$に対し，次は同値である．
- $f$は$X$上で連続．
- 任意の開集合$O\subset Y$に対し，$f^{-1}(O)$は$X$の開集合．
[$(1)\Ra(2)$の証明] 任意の開集合$O\subset Y$をとり，任意に$a \in f^{-1}(O)$をとる．
$a \in f^{-1}(O)$より$f(a)\in O$であり，$O$は開だから，ある$\epsilon>0$が存在して
をみたす．条件１が成り立っていれば$f$は点$a$で連続なので，上の$\epsilon$に対して，ある$\delta>0$が存在して
が成り立つ．すなわち，任意の$x\in U_{\delta}(a)$は$f(x)\in U_{\epsilon}(f(a))$をみたす．よって，
となって，$U_{\delta}(a)\subset f^{-1}(O)$を得る．よって，定義から$f^{-1}(O)$は$X$の開集合である．
[$(2)\Ra(1)$の証明] 任意の$a\in X$をとり，任意に$\epsilon>0$をとる．
$U_{\epsilon}(f(a)) \subset Y$は開集合なので，条件２が成り立っていれば$f^{-1}\left(U_{\epsilon}(f(a))\right)$も$X$の開集合である．
さらに，もとより$a \in f^{-1}\left(U_{\epsilon}(f(a))\right)$であるから，ある$\delta>0$が存在して
が成り立つ．よって，$f(U_{\delta}(a)) \subset U_{\epsilon}(f(a))$が成り立つ．
これは任意の$x\in U_{\delta}(a)$が$f(x)\in U_{\epsilon}(f(a))$を満たすことに他ならない．言い換えれば，$d_1(x,a)<\delta$を満たす任意の$x\in X$が
を満たすことに他ならないから，定義から$f$は$a$で連続である．$a$は$X$上の任意の点だったから$f$は$X$上で連続である．
位相空間の連続写像
ここで重要なことは，上の定理[連続写像の同値条件]の２つ目の条件は距離空間でない一般の位相空間にも通用するという点です．
つまり，一般の位相空間上の写像の連続性を定理[連続写像の同値条件]の２つ目の条件により定めれば，既に距離空間で定めていた写像の連続性の定義と矛盾しませんね．
[位相空間上の連続写像] 位相空間$X$, $Y$に対し，写像$f:X\rightarrow Y$が連続であるとは次が成り立つことをいう：任意の開集合$U \subset Y$に対し，$f^{-1}(U)$は$X$の開集合．
このことは，標語的に「開集合の連続写像による引き戻しは開集合」ということが多いですね．
証明は省略しますが，この「開集合」を「閉集合」に変えた次の「閉集合の連続写像による引き戻しは閉集合」も成り立ちます．
[連続写像の同値条件’] 距離空間$(X,d_1),(Y,d_2)$と写像$f:X\to Y$に対し，次は同値である．
- $f$は$X$上で連続．
- 任意の閉集合$U \subset Y$に対し，$f^{-1}(U) \subset X$は閉集合．
この定理[連続写像の同値条件’]の２つ目の条件を連続写像の定義とすることもできますが，慣習的に開集合の引き戻しによって連続写像を定義するのが普通です．
参考文献
集合・位相入門
[松坂和夫 著/岩波書店]
本書は「集合論」「位相空間論」をこれから学ぶ人のための入門書です．
説明が丁寧で行間が少ないのは初学者にありがたいところですね．
実際，本書は1968年に発刊されて以来売れ続けている超ロングセラーで，2018年に新装版が発売されたことからも現在でも教科書として広く使われていることが分かります．
具体例が多く扱われているのも特徴で，新しい概念のイメージも掴みやすいように書かれています．
また，各セクションの終わりに少なくない数の演習問題も載っており，演習書的な使い方もできます．
なお，本書については，以下の記事で書評としてまとめています．
【オススメの教科書｜集合・位相入門(松坂和夫著，岩波書店)】
本書の目次・必要な知識・良い点と気になる点・オススメの使い方などをレビューしています．
集合と位相
[鎌田正良 著/近代科学社(現代数学ゼミナール)]
本書はすっきりと書かれた「集合論」「位相空間論」の教科書です．
簡潔な説明が多いので，集合と位相の基本の全体像をさらうのに適しています．
裏返せば簡潔すぎてかえって分かりにくい可能性もありますが，数学をきちんと学びたい人には是非読みこなして欲しいテキストです．
また，演習問題の解説も丁寧に書かれているので，この点は独学で学ぶ場合には重宝します．
背景にある位相の圏論的な性質も踏まえて解説されており，数学系の学生は是非とも理解しておきたい考え方です．
コメント