集合論には二項関係という概念がありますが,二項関係の中でもある性質を満たすものを同値関係といいます.
最初に「同値関係」と聞くと語感からキツい印象を受けてしまいますが,実際にはただの「グループ分け」の考え方を数学的に定式化したものにほかなりません.
とはいえ,同値関係は数学の様々な分野に現れる概念であり,縁の下の力持ちともいえます.例えば
- 代数学では剰余群$G/N$
- 幾何学では射影空間$\K P_n$
- 解析学ではLebesgue(ルベーグ)空間$L^p(\R^n)$
などは商集合の一種で,定義には同値関係が必要です.
この記事では,同値関係の基本的な考え方と,同値関係の具体例を考えます.
同値関係
ここでは
- 二項関係
- 同値関係
を説明します.
二項関係
まずは二項関係の定義です.
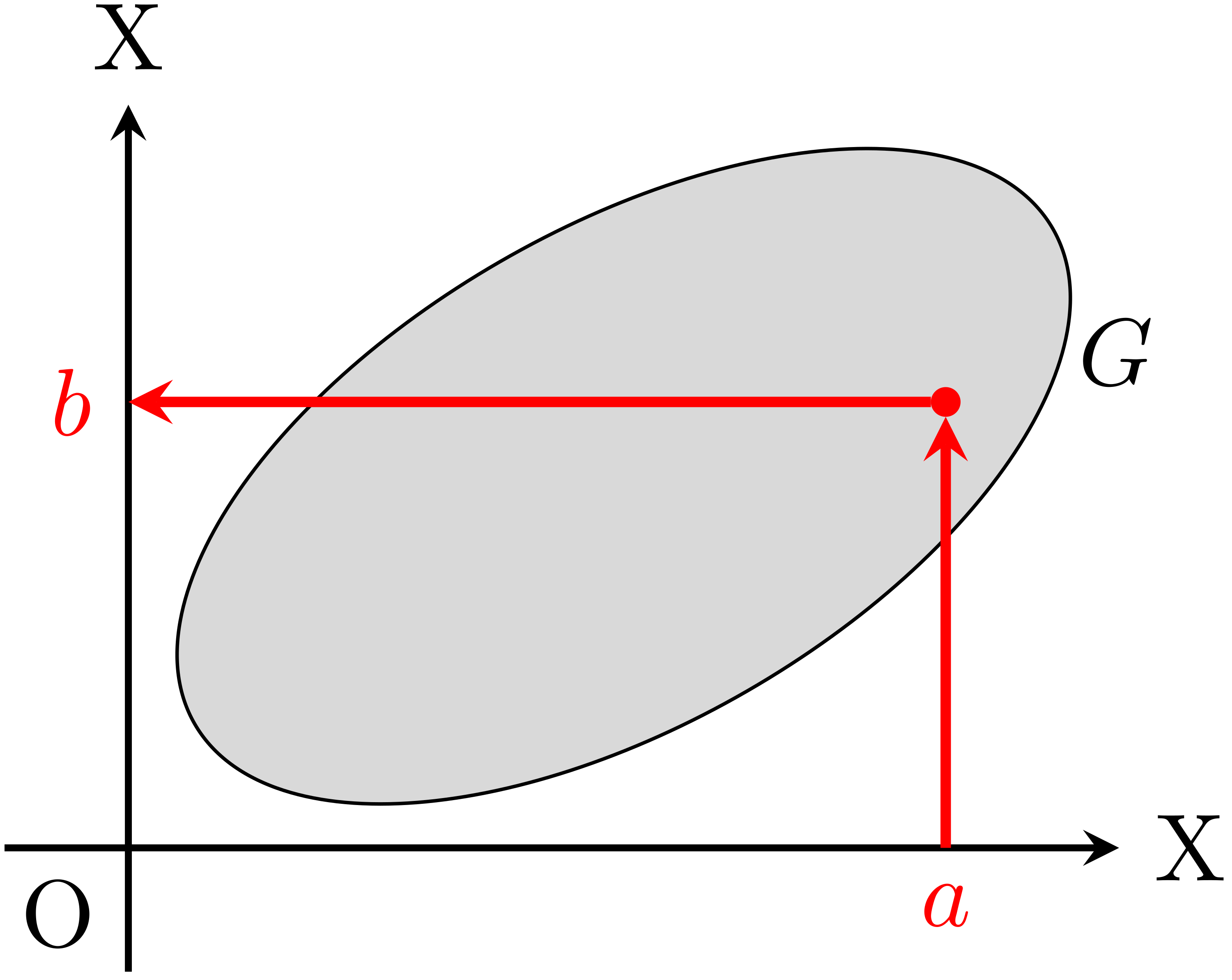
集合$X$に対して,$G\subset X\times X$とする.このとき,組$R:=(X,G)$を$X$上の二項関係 (binary relation)または単に関係 (relation)という.また,$(a,b)\in G$のとき$aRb$などと表し,$a$, $b$は関係$R$をもつという.
逆に,$(a,b)\in X$がある条件を満たすとき$a\hat{R}b$で表し,
\begin{align*}
G:=\set{(a,b)\in X\times X}{a\hat{R}b},\quad
R:=(X,G)
\end{align*}
とすれば$aRb=a\hat{R}b$となります.つまり,
- $G\subset X\times X$を定めること
- $(a,b)\in X\times X$がみたす条件$aRb$を定めること
はどちらも二項関係を定めていることになるわけですね.
例1
$\R$上の二項関係$R$を
\begin{align*}
aRb
\stackrel{\mrm{def.}}{\iff} a<b
\end{align*}
で定めると,$R:=(\R,G)$で定まる$G\subset\R\times\R$は
\begin{align*}
G:=\set{(a,b)\in\R\times\R}{a<b}
\end{align*}
となります.
例2
$\R$上の二項関係$R$を
\begin{align*}
aRb
\stackrel{\mrm{def.}}{\iff} a=b
\end{align*}
で定めると,$R:=(\R,G)$で定まる$G\subset\R\times\R$は
\begin{align*}
G:=\set{(a,b)\in\R\times\R}{a=b}
\end{align*}
となります.
例3
$[0,1]$上の二項関係$R$を
\begin{align*}
aRb
\stackrel{\mrm{def.}}{\iff} a=b\ \text{or}\ (a,b)=(0,1),(1,0)
\end{align*}
で定めると,$R:=([0,1],G)$で定まる$G\subset[0,1]\times[0,1]$は
\begin{align*}
G:=\set{(a,b)\in[0,1]\times[0,1]}{a=b\ \text{or}\ (a,b)=(0,1),(1,0)}
\end{align*}
となります.
同値関係
次に同値関係を説明します.
集合$X$上の二項関係$R$が次の3条件を満たすとき,$R$を同値関係 (equivalence relation)という.
- 反射性:任意の$a\in X$に対して,$aRa$が成り立つ.
- 対称性:任意の$a,b\in X$が$aRb$を満たせば,$bRa$が成り立つ.
- 推移性:任意の$a,b,c\in X$が$aRb$かつ$bRc$を満たせば,$aRc$が成り立つ.
同値関係は$R$よりも$\sim$などの記号で表すことが普通なので,ここから同値関係は$\sim$で表します.
さて,これらの3条件を平たくいえば,
- 全ての$a\in X$は自身と関係を持ち
- 関係$\sim$にある$X$の元は互いに行き来することができ
- 別の元を経由して辿り着けるものとも関係をもつ
というわけですね.
このことから,同値関係$\sim$で繋がっている元たちは1つの「グループ」を作っていることになります.
言い換えれば,同値関係$\sim$で繋がっていない元たちはどう頑張っても$\sim$では行き来できないわけですね.
先ほどの例では,例2と例3の関係$R$は同値関係です.
この「グループ」を数学では次のように定義します.
集合$X$上の同値関係$\sim$に対して,$X=\bigcup_{M\in\mathfrak{M}}M$を満たす$X$の部分集合族
\begin{align*}
\mathfrak{M}:=\set{M\subset X}{\begin{gathered}\all a,b\in M\ a\sim b,\\ \all a\in M\ \all b\notin M\ a\nsim b\end{gathered}}
\end{align*}
を$X$の$\sim$による商集合 (quotient set)といい$X/\sim$と表す.また,$M\in\mathfrak{M}$のそれぞれを同値類 (equivalence class)という.
なお,$x\in X$が属する同値類を$[x]$と表すことがよくあります.
商集合の2つの条件については,
- $\all a,b\in M\quad a\sim b$は「同値類に属する元たちは全て関係をもつ」
- $\all a\in M\ \all b\notin M\ a\nsim b$は「異なる同値類に属する元は関係を持たない」
ということですね.
このように,集合$X$上に同値関係$\sim$が定まっていると自然に$\sim$によりグループ分けされた部分集合族$\mathfrak{M}$が定まり,この$\mathfrak{M}$を商集合$X/\sim$というわけですね.
また,$\mathfrak{M}=X/\sim$は「同値関係$\sim$で繋がった$X$の元の全てを同一視したもの」とも言い換えることができますね.
具体例
ここでは具体的に冒頭に挙げた
- 代数学では剰余群$G/N$
- 幾何学では射影空間$\K P_n$
- 解析学ではLebesgue空間$L^p(\R^n)$
を紹介します.
剰余群
剰余群$G/N$は次のように定義されます.
群$G$とその正規部分群$N$を考える.このとき,$G$上の同値関係
\begin{align*}
g\sim h\stackrel{\mrm{def.}}{\iff}g^{-1}h\in N
\end{align*}
による商集合$G/\sim$を$G/N$と表す.さらに,$g\in G$が属する$G/N$の同値類を$gN$で表し,$g_1N,g_2N\in G/N$の積を
\begin{align*}
(g_1N)(g_2N)=(g_1g_2)N
\end{align*}
で定めると,$G/N$は群となる.この群$G/N$を剰余群 (quotient group)という.
この関係$\sim$が同値関係となっていること,すなわち同値関係の定義の
- 反射性
- 対称性
- 推移性
を証明しましょう.
[反射性] 任意の$g\in G$に対して
\begin{align*}
g^{-1}g=1_{G}=1_{N}\in N
\end{align*}
なので,$g\sim g$が成り立つ.ただし,$1_{G}$, $1_{N}$はそれぞれ$G$, $N$の単位元である.
[対称性] 任意の$g,h\in G$に対して,$g\sim h$が成り立つとする.このとき,$g^{-1}h\in N$なので
\begin{align*}
h^{-1}g=(g^{-1}h)^{-1}\in N
\end{align*}
が成り立つ.よって,$h\sim g$が成り立つ.
[推移性] 任意の$g,h,i\in G$に対して,$g\sim h$かつ$h\sim i$が成り立つとする.このとき,$g^{-1}h, h^{-1}i\in N$なので
\begin{align*}
g^{-1}i=g^{-1}(h^{-1}h)i=(g^{-1}h)(h^{-1}i)\in N
\end{align*}
が成り立つ.よって,$g\sim i$が成り立つ.
なお,剰余群の定義の詳しい考え方はwell-defined性の考え方とともに以下の記事で詳しく説明しています.
【剰余群の考え方を理解しよう|well-definedの確認】
群論を学ぶといずれ剰余群に出逢うことになりますが,剰余群の定義ではwell-defined性を確認することが大切です.この記事では,「可換群の剰余群」→「一般の群の剰余群」の順に,剰余群の考え方を説明しています.
射影空間
射影空間$\K P_n$は次のように定義されます.
正の整数$n$と位相体$\K$に対して,$\K^{n+1}\setminus{0}$上の同値関係
\begin{align*}
\m{a}\sim\m{b}
\stackrel{\mrm{def.}}{\iff} \exi t\in\K\ \mrm{s.t.}\ t\m{a}=\m{b}
\end{align*}
による商集合$\K^{n+1}\setminus\{0\}/\sim$を$\K P_n$と表す.さらに,$\bmat{a_1\\\vdots\\a_n}\in\K^{n+1}\setminus{0}$が属する$\K P_n$の同値類を$[a_1:\dots:a_n]$で表し,自然な写像
\begin{align*}
\K^{n+1}\setminus\{0\}\to\K P_n;\bmat{a_1\\\vdots\\a_n}\longmapsto[a_1:\dots:a_n]
\end{align*}
が連続になる最小の位相により$\K P_n$は自然に位相空間となる.この位相空間$\K P_n$を射影空間 (projective space)という.
位相体$K$は例えば$K=R,C$のことで,
- $\R P_n$を実射影空間
- $\C P_n$を複素射影空間
といいます.
$\m{a},\m{b}\in\K^{n+1}\setminus\{0\}$が$t\m{a}=\m{b}$となる$t\in\K$をもつためには,$\m{a}$, $\m{b}$が$\K^{n+1}$の原点を通る同一直線上に存在することが必要十分です.
よって,射影空間$\K P_n$は$\K^{n+1}\setminus{0}$の原点を通る直線上の零ベクトルでないベクトルを同一視したものと言えますね.
射影空間$\K P_n$の定義で考えたように,一般に以下のように定義します.
位相空間$X$上の同値関係$\sim$に対して,自然な写像
\begin{align*}
X\to X/\sim;x\longmapsto[x]
\end{align*}
が連続になる$X/\sim$の最小の位相を商位相 (quotient topology)といい,商位相が定まった$X/\sim$を商空間 (quotient topological space)という.
よって,位相空間$\K P_n$は「$\K^{n+1}$の同値関係$\sim$による商空間」と表現することができますね.
Lebesgue空間
Lebesgue(ルベーグ)空間$L^p(\R^n)$は次のように定義されます.
$\mu$をLebesgue測度,$p\ge1$とする.$\R^n$上の実数値関数で$p$乗Lebesgue可積分な関数の空間
\begin{align*}
\mathcal{L}^p(\R^n):=\set{f:\R^n\to\R}{\int_{\R^n}|f(x)|^p\,dx<infty}
\end{align*}
に対して,$\mathcal{L}^p(\R^n)$上の同値関係
\begin{align*}
f\sim g
\stackrel{\mrm{def.}}{\iff} \mu(\set{x\in\R^n}{f(x)\neq g(x)})=0
\end{align*}
による商集合$\mathcal{L}^p(\R^n)/\sim$を$L^p(\R^n)$と表す.さらに,$L^p(\R^n)$に和と$\R$倍を
- 和:$[f]+[g]=[f+g]$
- $\R$倍:$\alpha[f]=[\alpha f]$
を定めると$L^p(\R^n)$は線形空間となり,ノルムを
\begin{align*}
\|[f]\|_{p}:=\bra{\int_{\R^n}|f(x)|^p\,dx}^{1/p}
\end{align*}
で定めることにより$L^p(R^n)$はBanach(バナッハ)空間となる.このBanach空間$L^p(\R^n)$をLebesgue空間という.
$\mu(\set{x\in\R^n}{f(x)\neq g(x)})=0$は「$f(x)$と$g(x)$が異なるような$x\in\R^n$のLebesgue測度$\mu$による長さ(測度)が0である」ということですね.
このことは「$f$と$g$はほとんど至るところで等しい」とも表現できるのでした.
なお,$f,g\in\mathcal{L}^{p}(\R^n)$がほとんど至るところで等しければ積分の値も変わりませんから,$[f]\in L^p(\R^n)$のことを普通の関数のように単に$f$と表します.
また,上の定義の和と$\R$倍で線形空間になることは簡単ですが,ノルム$\|\cdot\|_{p}$によりBanach空間となることを示すのは少々大変(であり,本筋とはかなり違う)なのでここでは説明しません.

コメント