ツォルン(Zorn)の補題は選択公理と同値な存在定理で,ツォルンの補題を用いることで様々なものの存在を証明することができます.
例えば,この記事で扱う
- 任意の線形空間における基底
- ハメル(Hamel)基底
はどちらもツォルンの補題によって存在を証明することができます.
ハメル基底のイメージなどについては以下の記事でも説明しているので参照してください.
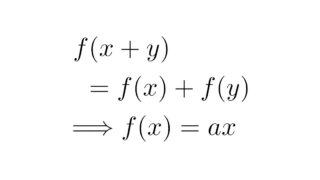
参考文献
集合・位相入門
[松坂和夫 著/岩波書店]
本書は「集合論」「位相空間論」をこれから学ぶ人のための入門書です.
本書は説明が丁寧で行間が少ないテキストなので,初学者にとっても読みやすくなっています.
実際,本書は1968年に発刊されて以来売れ続けている超ロングセラーで,2018年に新装版が発売されたことからも現在でも広く使われていることが分かります.
具体例が多く扱われているのも特徴で,新しい概念のイメージも掴みやすいように書かれています.
また,各セクションの終わりに少なくない数の演習問題も載っており,演習書的な使い方もできます.
なお,本書については,以下の記事で書評としてまとめています.
【オススメの教科書|集合・位相入門(松坂和夫著,岩波書店)】
本書の目次・必要な知識・良い点と気になる点・オススメの使い方などをレビューしています.
ツォルンの補題
ツォルンの補題の前に準備として定義をいくつか確認しておきましょう.
集合$X$上に定義された二項関係$\le$が次の1〜3が満たされるとき,$(X,\le)$ (または単に$X$)を順序集合 (ordered set)という.
- 任意の$a\in X$に対して$a\le a$
- $a\le b$かつ$b\le c$を満たす任意の$a,b,c\in X$に対して$a\le c$
- $a\le b$かつ$b\le a$を満たす任意の$a,b\in X$に対して$a=b$
さらに,次の4が満たされるとき,$(X,\le)$ (または単に$X$)を全順序集合 (totally ordered set)という.
- 任意の$a,b\in X$に対して$a\le b$または$b\le a$
性質1を反射律,性質2を推移律,性質3を反対称律,性質4を全順序律ということがあります.
$X$が順序集合といった場合には,比較できない$X$の2元が存在しても構いません.順序集合のうちでも任意の$X$の2元が比較できるときには,$X$をとくに全順序集合というわけですね.
なお,全順序集合と区別するために,全順序でない順序集合を半順序集合ということもあります.
この記事で単に「順序集合」と書いた場合には,全順序でも全順序でなくてもよいとします.
順序集合$X$の任意の全順序部分集合$Y$が$X$に上界を持つとき,$X$は帰納的であるという.
順序集合$X$が空でないとき,任意の$x\in X$に対して$\{x\}$は$X$の全順序部分集合なので,$X$の部分集合であって全順序集合であるものは必ず存在しますね.
このように$X$の部分集合であって全順序集合であるものは常に存在しますが,それらのどの全順序部分集合も$X$上に上界をもつとき$X$を帰納的順序集合というわけですね.
すなわち,任意の全順序部分集合$Y\subset X$に対し,任意の$y\in Y$に対して,$y\le x$となる$x\in X$が存在することをいうわけですね.
[ツォルンの補題]空でない帰納的順序集合は(少なくとも1つ)極大元をもつ.
ツォルンの補題によって示される極大元は1つとは限りません.つまり,極大元は複数存在することもあります.
基底の存在の証明
ツォルンの補題を使って
- 線形空間の基底
- ハメル基底
の存在を示しますが,その前に次の基本的な事柄を確認しておきます.
集合族は包含関係$\subset$により順序集合となる.
集合族とは「集合の集合」のことですね.
$\mathcal{X}$を集合族とする.
- 任意の$A\subset\mathcal{X}$に対して,$A\subset A$だから,反射律が成り立つ.
- $A\subset B,B\subset C$を満たす任意の$A,B,C\subset\mathcal{X}$に対して,$A\subset C$だから,推移律が成り立つ.
- $A\subset B,B\subset A$を満たす任意の$A,B\subset\mathcal{X}$に対して,$A=B$だから,反対称律が成り立つ.
よって,$(\mathcal{X},\subset)$は順序集合である.
線形空間の基底とその存在証明
まずは線形空間の基底の定義を見ておきます.
線形空間$V$に対して,$V$の部分集合$B$が基底であるとは,次を満たすことをいう:
- 任意の有限個の$b_1,\dots,b_n\in B$に対して,$b_1,\dots,b_n$は線形独立である.
- 任意の$v\in V$に対して,有限個の$b_1,\dots,b_n\in B$が存在して,$v$は$b_1,\dots,b_n$の線形結合で表せる.
$V$は有限次元とは限らないので$B$の元の個数が有限個であるとは限りません.
さて,この定義は「2つの条件を満たすものを基底という」と述べているだけで,全ての線形空間が基底をもつかどうかについては何も言っていません.
ところが,ツォルンの補題を用いれば「全ての線形空間に基底が存在すること」が証明できます.
$\{0\}$でない任意の線形空間は基底をもつ.
$\mathbb{F}$を体,$V$を$\{0\}$でない$\mathbb{F}$上の線形空間とする.この$V$が基底をもつことを示す.
次を満たす$V$の部分集合$B$の族を$\mathcal{B}$とする:任意の有限個の$b_1,\dots,b_n\in B$に対して,$b_1,\dots,b_n$は線形独立である.
[1]$\mathcal{B}$が包含に関して極大元をもつことを示す.
集合族は包含関係に関して順序集合となることは,上の命題で示した.また,$V$は$\{0\}$ではないから,$v\in V\setminus\{0\}$が存在する.このとき,集合$\{v\}$からとれる有限個の元は$v$のみであり,$v$は線形独立だから,$\mathcal{B}$は空でない.
よって,あとは$\mathcal{B}$が帰納的であることを示せば,ツォルンの補題により$\mathcal{B}$は包含に関して極大元をもつことが分かる.すなわち,任意の全順序部分集合$\mathcal{A}\in\mathcal{B}$に対して,$\mathcal{A}$の上界が$\mathcal{B}$に存在することを示せばよい.
$A_{*}\subset V$を
\begin{align*}A_{*}:=\bigcup_{A\subset\mathcal{A}}A\end{align*}
で定める.
このとき,$A_{*}$が$\mathcal{A}$の上界であることは明らかだから,$A_{*}\in\mathcal{B}$を示せばよい.
任意の有限個の$a_1,\dots,a_n\in A_{*}$に対して,$a_k\in A_k$となる$A_k\in\mathcal{A}$が存在する($k\in\{1,\dots,n\}$).いま$\mathcal{A}$は全順序集合だから,ある$k_{*}\in \{1,\dots,n\}$が存在して,任意の$k\in\{1,\dots,n\}$に対して$A_k\subset A_{k_{*}}$が成り立つ.
よって,$a_1,\dots,a_n\in A_{k_{*}}$が成り立ち,$A_{k_{*}}\in\mathcal{B}$だから$a_1,\dots,a_n$は線形独立である.
以上より,$A_{*}\in\mathcal{B}$が従う.
[2]$\mathcal{B}$の包含に関する極大元が$V$の基底となることを背理法により示す.すなわち,$\mathcal{B}$の包含に関する任意の極大元を$B$とし,$B$の有限個の元の線形結合で表せない$v\in V$が存在するとして矛盾を導く.
このとき,$B’:=B\cup\{v\}$とする.$B’$から任意の有限個の元$b_1,\dots,b_n$をとる.
$b_1,\dots,b_n\in B$なら,$B\in\mathcal{B}$から$b_1,\dots,b_n$は線形独立である.
ある$k\in\{1,\dots,n\}$に対して$b_k=v$なら,$c_1b_1+\dots+c_nb_n=0$ ($c_1,\dots,c_n\in \mathbb{F}$)のとき$c_k=0$である.実際,$c_k\neq0$なら,両辺を$c_k$で割って$v$を移項することにより,$v$が$B$の元の線形結合で表せることになり矛盾するから,$c_k=0$である.
したがって,$B’\in\mathcal{B}$が従う.これは,$B$が$\mathcal{B}$の極大元であることに矛盾する.よって,$\mathcal{B}$の包含に関する極大元は$V$の基底となる.
ハメル基底とその存在証明
ハメル基底は次のように定義されます.
次を満たす$B\subset\R$をハメル基底という:
- 任意の有限個の$b_1,\dots,b_n\in B$に対して,$r_1b_1+\dots+r_nb_n=0\ (r_1,\dots,r_n\in\Q)$なら$r_1=\dots=r_n=0$が成り立つ.
- 任意の$x\in\R$に対して,有限個の$b_1,\dots,b_n\in B$と同数の$r_1,\dots,r_n\in\Q$が存在して,$x=r_1b_1+\dots+r_nb_n$と表せる.
線形代数の言葉で言えば,ハメル基底は体$\Q$上の(無限次元)線形空間$\R$の基底ということができますね.
ただし,この定義も「ハメル基底はこういうものとする」ということを述べただけで,ハメル基底が存在するかどうかは別の話です.
しかし,やはりハメル基底も上の線形空間の基底の存在の証明で$V=\R$, $\mathbb{F}=\Q$と見ることにより,同様に議論を進めることができます.
ハメル基底は存在する.
次を満たす$\R$の部分集合の族を$\mathcal{B}$とする:任意の有限個の$b_1,\dots,b_n\in\mathcal{B}$に対して,$r_1b_1+\dots+r_nb_n=0$ ($r_1,\dots,r_n\in\Q$)なら$r_1=\dots=r_n=0$が成り立つ.
[1]$\mathcal{B}$が包含に関して極大元をもつことを示す.
集合族は包含関係に関して順序集合となることは,上の命題で示した.また,$x\in\R\setminus\{0\}$に対して,$rx=0\ (r\in\Q)$なら$r=0$だから$\{x\}\in\mathcal{B}$となって,$\mathcal{B}$は空でない.
よって,あとは$\mathcal{B}$が帰納的であることを示せば,ツォルンの補題により$\mathcal{B}$は包含に関して極大元をもつことが分かる.すなわち,任意の全順序部分集合$\mathcal{A}\in\mathcal{B}$に対して,$\mathcal{A}$の上界が$\mathcal{B}$に存在することを示せばよい.
$A_{*}\subset\R$を
\begin{align*}A_{*}:=\bigcup_{A\subset\mathcal{A}}A\end{align*}
で定める.
このとき,$A_{*}$が$\mathcal{A}$の上界であることは明らかだから,$A_{*}\in\mathcal{B}$を示せばよい.
任意の有限個の$a_1,\dots,a_n\in A_{*}$に対して,$a_k\in A_k$となる$A_k\in\mathcal{A}$が存在する($k\in\{1,\dots,n\}$).いま$\mathcal{A}$は全順序集合だから,ある$k_{*}\in\{1,\dots,n\}$が存在して,任意の$k\in\{1,\dots,n\}$に対して$A_k\subset A_{k_{*}}$が成り立つ.
よって,$a_1,\dots,a_n\in A_{k_{*}}$が成り立ち,$A_{k_{*}}\in\mathcal{B}$だから$a_1,\dots,a_n$は線形独立である.
以上より,$A_{*}\in\mathcal{B}$が従う.
[2]$\mathcal{B}$の包含に関する極大元がハメル基底となることを背理法により示す.すなわち,$\mathcal{B}$の包含に関する任意の極大元を$B$とし,$r_1b_1+\dots+r_nb_n$ ($r_1,\dots,r_n\in\Q$, $b_1,\dots,b_n\in B$)の形で表せない$x\in V$が存在するとして矛盾を導く.
このとき,$B’:=B\cup\{x\}$とする.$B’$から任意の有限個の元$b_1,\dots,b_n$をとる.
$b_1,\dots,b_n\in B$なら,$B\in\mathcal{B}$から$r_1b_1+\dots+r_nb_n=0$のとき$r_1=\dots=r_n$である.
ある$k\in\{1,\dots,n\}$に対して$b_k=x$なら,$r_1b_1+\dots+r_nb_n=0$ ($r_1,\dots,r_n\in \Q$)のとき$r_k=0$である.実際,$r_k\neq0$なら,両辺を$r_k$で割って$x$を移項することにより,$x$が
\begin{align*}r’_1b_1+\dots+r’_{k-1}b_{k-1}+r’_{k+1}b_{k+1}+\dots+r’_nb_n\end{align*}
の形で表せることになり矛盾するから,$r_k=0$である.
したがって,$B’\in\mathcal{B}$が従う.これは,$B$が$\mathcal{B}$の極大元であることに矛盾する.よって,$\mathcal{B}$の包含に関する極大元はハメル基底である.
なお,ハメル基底はもともと「$f(x+y)=f(x)+f(y)$を満たす関数が$f(x)=ax$と表されるもの以外に存在するか?」という問題の反例を構成するために考えられました.
この反例については以下の記事を参照してください.
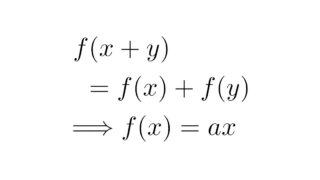



コメント
$\{0\}$でない任意のベクトル空間は基底をもつって本当ですか?
例えば実数の無限数列ってベクトル空間と見なせますけど、一般に基底のうち有限個を選んでも数列をその線型結合で表せないと思います。
ご質問をありがとうございます.
例示して頂いた実数列の空間を$\ell(\R)$とすると,
\begin{align*}
A:=\set{e_n\in\ell(\R)}{n\in\N}
\end{align*}
は$\ell(\R)$の基底ではありません($e_n$は第$n$成分のみ1の実数列とします).しかし,$A$の任意の有限個の元は線型独立です.
ここで,$A$に全ての成分が$1$の数列$a:=(1,1,1,\dots)$を加えた集合を$A_{1}$とします:
\begin{align*}
A_{1}:=A\cup\{a\}.
\end{align*}
このとき,$A_{1}$も$\ell(\R)$の基底ではありませんが,$A_{1}$の任意の有限個の元は線型独立です.
続いて,$A_{1}$に$b:=(1,2,3,\dots)$と第$n$成分が$n$の数列を付加した集合を$A_{2}$とします.
\begin{align*}
A_{2}:=A_{1}\cup\{b\}=A\cup\{a,b\}.
\end{align*}
このとき,$A_{2}$もやはり$\ell(\R)$の基底ではありませんが,$A_{2}$の任意の有限個の元は線型独立です.
基底の存在の証明にZornの補題(⇔選択公理)が必要となるのは,お気付きのように無限次元の場合ですが,今見たように無限次元の場合には線型独立なベクトルをどんどん加えていくことができます.
Zornの補題(⇔選択公理)が必要な存在証明は具体的構成は一般に困難ですので,この$\ell(\R)$の基底を具体的に構成することは難しいです.
しかし,「うまく線型独立なベクトルを(無限に)増やしていくことができれば,$\ell(\R)$の任意の元が有限個のベクトルの和で表せるようになる」と考えれば分かりやすいかも知れません.
大変丁寧な回答ありがとうございます.量子論で無限次元の複素ヒルベルト空間が出てきたので気になっていました.
有限次元の場合からの類推から、Aが基底になるはずだがならないので基底は存在しない、と思い込んでいましたが、単なる思い込みでした.確かに、うまくAに無限にベクトルを追加すれば基底になるかもしれない(実際になる)と思いました.
有限次元と無限次元の違いが浮き彫りになる感じですごいと思います.
ご返信をありがとうございます.
ご納得頂けたようで安心しました.
有限次元の類推が無限次元にそのまま通用するとは限らないのは,無限次元の難しさでもあり,面白さですよね.