線形空間に対して線形部分空間が定義されたように,群に対しても部分群というものが定義されます.
名前からも分かるように,部分群とは
- もとの群の集合の部分集合で
- もとの群と同じ演算で閉じていて
- 群となっているもの
のことを言います.
この記事では
- 部分群の定義・具体例
- 部分群の性質・証明のテンプレート
を順に解説します.
「群論の基本」の一連の記事
- 群と部分群
- 1 群の定義・考え方を具体例から解説
- 2 部分群の証明のテンプレを例題から理解する (今の記事)
- 3 生成される部分群・巡回群の定義と具体例
- 剰余類とラグランジュの定理|部分群の位数(準備中)
- 可換群の剰余群を具体例から丁寧に理解する(準備中)
- 正規部分群は非可換群の剰余群で超重要(準備中)
- 群の準同型
- 群の準同型は群の演算を保つ大切な写像(準備中)
- 群の準同型の像Im(f)と核Ker(f)の定義と例題(準備中)
- 群の準同型定理の考え方を例題から掴む(準備中)
部分群の定義・具体例
まずは部分群の定義を述べ,具体例を考えましょう.
演算が閉じているとは?
部分群を定義するために,「演算が閉じている」という言葉を定義しておきます.
群$(G,\cdot)$と$H\subset G$を考える.任意の$h_1,h_2\in H$に対して$h_1\cdot h_2\in H$が成り立つとき,$H$は演算・について閉じているという.
群の定義から,群$(G,\cdot)$の演算・は$G$の2元を与えるとただひとつの$G$の元を返す写像$G\times G\to G$ですから,任意の$h_1, h_2\in H\subset G$に対して$h_1\cdot h_2\in G$となることは当たり前です.
ところが,うまく$H\subset G$をとると,どんな$h_1, h_2\in H\subset G$に対しても$h_1\cdot h_2\in H$となることがあります.
このように,$H$の2元を与えると結果が$H$からはみ出さないとき,演算・は$H$で閉じているというわけですね.
部分群の定義
ざっくり言えば,群$G$と$H\subset G$に対して,$H$が$G$と同じ演算で群になっているとき,$H$を$G$の部分群といいます.
このことをきちんと書くと次のようになります.
群$(G,\cdot)$と$H\subset G$に対し,$H$が$G$の演算で閉じているとする.
このとき,$H$が演算・により群となっていれば,$(H,\cdot)$を$(G,\cdot)$の部分群(subgroup)という.
正確には$\cdot:G\times G\to G$の定義域を$H\times H$に制限してできる演算を$\star:H\times H\to H$とするときの$(H,\star)$が群$(G,\cdot)$の部分群です.
定義域が異なる写像は異なる写像と考えるのでしたから・と$\star$は本来異なるものですが,慣習的に$\star$も・で表すのが普通です.
大切なことは,部分群$(H,\cdot)$の演算がもとの群$(G\cdot)$の演算に由来しているということです.
つまり,$H\subset G$であっても,$G$上の演算と$H$上の演算が異なっていれば,部分群とは言わないことに注意してください.
具体例1($(\Z,+)$の部分群)
整数全部の集合と通常の加法の群$(\Z,+)$を考えます.$\Z$の部分集合として,偶数全部の集合
\begin{align*}2\Z=\set{2n\in\Z}{n\in\Z}=\{\dots,-4,-2,0,2,4,\dots\}\end{align*}
を考えます.
任意の$2m,2n\in2\Z$($m,n\in\Z$)に対して
\begin{align*}2m+2n=2(m+n)\in2\Z\end{align*}
ですから,$2\Z$は加法+について閉じていますね.さらに,$2\Z$において
- 加法+は結合法則を満たす
- 任意の$2n\in2\Z$($n\in\Z$)に対して$0+2n=2n+0=2n$が成り立つ(単位元は0)
- 任意の$2n\in2\Z$($n\in\Z$)に対して$2n+(-2n)=(-2n)+2n=0$が成り立つ($2n$の逆元は$-2n$)
の3性質をもつので,$(2\Z,+)$は$(\Z,+)$の部分群と分かりました.さらに,もとの$(\Z,+)$は可換群なので,$2\Z$上でも加法+は可換となり$(2\Z,+)$も可換群ですね.
具体例2($(\R\setminus\{0\},\times)$の部分群)
0を除く実数全部の集合と通常の乗法の群$(\R\setminus\{0\},\times)$を考えます.
一般に集合$A$, $B$に対して,$B$に属さない$A$の元全部の集合を$A\setminus B$と表しますね.
$\R\setminus\{0\}$の部分集合として,1と−1のみからなる集合$H=\{1,-1\}$を考えます.
\begin{align*}&1\times1=(-1)\times(-1)=1\in H,
\\&1\times(-1)=(-1)\times1=-1\in H\end{align*}
ですから,$H$は乗法$\times$について閉じていますね.さらに,$H$において
- 乗法$\times$は結合法則を満たす
- 任意の$x\in H$に対して$1\times x=x\times 1=x$が成り立つ(単位元は1)
- $1\times 1=1$, $(-1)\times(-1)=1$が成り立つ(1の逆元は1で,−1の逆元は−1)
の3性質をもつので,$(H,\times)$は$(\R\setminus\{0\},\times)$の部分群と分かりました.さらに,もとの群$(\R\setminus\{0\},\times)$は可換群なので,$H$上でも乗法$\times$は可換となり部分群$(H,\times)$も可換群ですね.
具体例3(非可換な部分群)
実数成分の$n$次正則行列全部の集合と通常の乗法の群$(\mrm{GL}_n(\R),\cdot)$を考えます.この群を(実数成分の)一般線形群というのでした.
$(\mrm{GL}_n(\R),\cdot)$の部分群として,行列式が1の実数成分の$n$次正則行列全部の集合$H$を考えます:
\begin{align*}H=\set{A\in\mrm{GL}_n(\R)}{|A|=1}\end{align*}
任意の$A,B\in H$に対して,
\begin{align*}|AB|=|A||B|=1\cdot1=1\end{align*}
となり$AB\in H$が成り立ちます.すなわち,$H$は乗法・について閉じていますね.
一般に行列式の性質として,任意の$n$次正方行列$A$, $B$に対して$|AB|=|A||B|$が成り立つのでした.
さらに,$H$において
- 演算・は結合法則を満たす
- 任意の$A\in H$に対して$AI_n=I_nA=e$が成り立つ(単位元は$n$次単位行列$I_n$)
- $AA^{-1}=A^{-1}A=e$が成り立つ($A$の逆元は$A$の逆行列$A^{-1}$)
の3性質をもつので,$(H,\cdot)$は$(\mrm{GL}_n(\R),\cdot)$の部分群と分かりました.ただし,例えば
\begin{align*}A=\sbmat{1&1\\0&1},\quad B=\sbmat{0&1\\-1&0}\in H\end{align*}
に対して
\begin{align*}AB=\sbmat{-1&1\\-1&0},\quad BA=\sbmat{0&1\\-1&-1}\end{align*}
なので,$AB\neq BA$だから$H$は非可換群ですね.
一般にこの非可換群$H$を(実数成分の)特殊線形群(special linear group)といい,$(\mrm{SL}_n(\R),\cdot)$と表します.
具体例4(自明な部分群)
$(G,\cdot)$を群とし,この群の単位元を$e$とします.このとき,$G$の部分集合として,単位元のみからなる部分集合$\{e\}$を考えます.
単位元の定義から
\begin{align*}e\times e=e\end{align*}
なので,$\{e\}$は演算・について閉じていますね.さらに,$\{e\}$において
の3性質をもつので,$(\{e\},\cdot)$は$(G,\cdot)$の部分群と分かりました.
どんな群に対しても$(\{e\},\cdot)$は部分群となるので,この単位元のみからなる集合の群$(\{e\},\cdot)$を自明な部分群といいます.
また,$G$の部分集合として$H:=G$全体を考えると,もとの$(G,\cdot)$が群ですから$(H,\cdot)$は部分群となります.
このように,どんな群$(G,\cdot)$に対しても$(G,\cdot)$自身は部分群となるので,この自分自身の群$(G,\cdot)$も自明な部分群といいます.
具体例5(部分集合だが,部分群でない例)
0を除く実数全部の集合と通常の加法の群$(\R,+)$と,部分集合$\R\setminus\{0\}\subset\R$を考えます.
$\R\setminus\{0\}$と通常の乗法の組$(\R\setminus\{0\},\times)$は群となりますが,群$(\R,+)$と群$(\R\setminus\{0\},\times)$では演算が異なっています.
このため,$(\R\setminus\{0\},\times)$は$(\R,+)$の部分群ではありません.
このように,親の群の演算と部分集合の群の演算が異なっていれば,部分群とはいえません.
部分群の性質・証明のテンプレート
上の具体例では,きちんと群の定義の条件を満たしていることを確認して,部分群であることを示しました.
しかし,実は群の定義の全てを確かめなくても良いことが分かります.
このことを用いて部分群であるための必要十分条件を考え,部分群であることの証明の具体例を見てみましょう.
部分集合上での結合法則
実は部分集合上で演算が閉じてさえいれば,結合法則は自動的に成り立ちます.
群$(G,\cdot)$に対して,部分集合$H\subset G$上で演算・が閉じていれば,$H$上で演算・は結合法則を満たす.
任意に$h_1,h_2,h_3\in H$をとる.$H$は$G$の部分集合だから$h_1,h_2,h_3\in G$である.$(G,\cdot)$は群なので,$G$上で・は結合法則を満たすから,
\begin{align*}(h_1h_2)h_3=h_1(h_2h_3)\end{align*}
が成り立つ.すなわち,$H$上で結合法則が成り立つ.
$G$で結合法則が成り立つので,もちろん$G$の一部である$H$でも結合法則が成り立つのは当たり前ですね.
部分群であるための必要十分条件
ざっくり言えば,群$(G,\cdot)$と$H\subset G$に対して,$H$が演算・で部分群となるための必要十分条件は
- $G$の単位元が$H$に属する($e_G\in H$)
- $H$は演算で閉じている($g,h\in H\Ra gh\in H$)
- $H$の任意の元の逆元も$H$に属する($g\in H\Ra g^{-1}\in H$)
を全て満たすことです.きちんと書けば次のようになります.
群$(G,\cdot)$に対して,部分集合$H\subset G$を考える.$(H,\cdot)$が$(G,\cdot)$の部分群であることの必要十分条件は,次の3条件を満たすことである.
- $G$の単位元$e_G$が$H$に属する.
- 演算・は$H$で閉じている.
- 任意の$h\in H$に対して,$G$における$h$の逆元$h^{-1}$が$H$に属する.
$(H,\cdot)$が$(G,\cdot)$の部分群であれば,$(H,\cdot)$は群だから3条件(1)-(3)を満たす.
よって,あとは十分性を示せば良い.すなわち,3条件(1)-(3)を満たすとして,$(H,\cdot)$が$(G,\cdot)$の部分群であることを示せばよい.
条件(1)より,・は(定義域を$H\times H$に制限すれば)$H$上の演算となっている.
[単位元の存在]任意に$h\in H$をとる.$H$は$G$の部分集合だから$h\in G$である.$G$における単位元$e_G$は
\begin{align*}he_G=e_Gh=h\end{align*}
を満たす.
[結合法則]上で示した補題から,条件(1)を満たしていれば$H$上で演算・は結合法則を満たす.
[逆元の存在]任意に$h\in H$をとる.$H$は$G$の部分集合だから$h\in G$である.$G$における$h$の逆元$h^{-1}$は
\begin{align*}hh^{-1}=h^{-1}h=e_G\end{align*}
を満たす.
以上より,3条件(1)-(3)を満たすなら,$(H,\cdot)$は$e_G$を単位元にもつ群となる.よって,$(H,\cdot)$は$(G,\cdot)$の部分群である.
要するに「親の群で結合法則が成り立っているので,部分集合でも自動的に結合法則が成り立つため,部分集合の方で結合法則が成り立っているかを確認する必要はない」ということですね.
また,証明からもわかるように,親の群の単位元は部分群での単位元にもなりますね.
可換群の部分群も可換群
結合法則と同様に,もとの群が可換なら部分群も可換となります.
可換群の部分群は可換群である.
可換群$(G,\cdot)$とその部分群$(H,\cdot)$を考え,任意に$h_1,h_2\in H$をとる.
$H$は$G$の部分集合だから$h_1,h_2\in G$である.$(G,\cdot)$は可換群なので,$G$上で・は交換法則を満たすから,
\begin{align*}h_1h_2=h_2h_1\end{align*}
が成り立つ.すなわち,$(H,\cdot)$は可換群である.
具体例6(部分群の証明)
群$(G,\cdot)$と$H\subset G$に対して,
- $G$の単位元が$H$に属する($e_G\in H$)
- $H$は演算で閉じている($g,h\in H\Ra gh\in H$)
- $H$の任意の元の逆元も$H$に属する($g\in H\Ra g^{-1}\in H$)
を示すのが,$(H,\cdot)$が$(G,\cdot)$の部分群になることの証明のテンプレートです.
0を除く実数全部の集合と通常の乗法の群$(\R\setminus\{0\},\times)$と,正の実数全部の集合$\R_+\subset\R\setminus\{0\}$を考える.$(\R_+,\times)$が$(\R\setminus\{0\},\times)$の可換部分群であることを示せ.
- $(\R\setminus\{0\},\times)$の単位元は1であり,1は正の実数なので$\R_+$に属する.
- 一般に2つの正の実数の積は正なので,任意の$a,b\in\R_+$に対して$ab\in\R_+$である.
- 任意の$a\in\R_+$に対して,$a$の$\R\setminus\{0\}$での逆元$1/a$は$\R_+$に属する.
よって,$(\R_+,\times)$は$(\R\setminus\{0\},\times)$の部分群である.
さらに,$(\R\setminus\{0\},\times)$は可換群なので,$(\R_+,\times)$も可換である.
具体例7(交代群)
一般に$n$次の置換全部の集合を$S_n$と表し,合成を積とする群を$n$次対称群というのでしたね.
対称群は重要な非可換群なので,「対称群」という言葉からすぐに「置換たちの群だ」と思えるようにしておきましょう.
偶置換は偶数個の互換の積で表される置換のことだった.
- $(S_n,\cdot)$の単位元は単位置換であり,単位置換は偶置換($(1,2)(1,2)$などと表せる)なので$A_n$に属する.
- 任意の$\sigma,\tau\in A_n$に対して,$\sigma=\iota_1\dots\iota_{2k}$, $\tau=\kappa_1\dots\kappa_{2\ell}$なる互換$\iota_1,\dots,\iota_{2k},\kappa_1,\dots,\kappa_{2\ell}\in S_n$が存在する.よって,
\begin{align*}\sigma\tau=\iota_1\dots\iota_{2k}\kappa_1\dots\kappa_{2\ell}\end{align*}
と積$\sigma\tau$は偶数個の互換の積で表されるから$\sigma\tau\in A_n$である. - 任意の$\sigma\in A_n$に対して,$\sigma=\iota_1\dots\iota_{2k}$なる互換$\iota_1,\dots,\iota_{2k}\in S_n$が存在する.よって,
\begin{align*}\sigma^{-1}=\iota_{2k}^{-1}\dots\iota_{1}^{-1}\end{align*}
と$\sigma^{-1}$は偶数個の互換の積で表されるから$\sigma^{-1}\in A_n$である.
よって,$(A_n,\cdot)$は$(S_n,\cdot)$の部分群である.
この部分群$(A_n,\cdot)$は$n$次交代群と呼ばれ,のちの記事で解説するように$n$次対称群の部分群の中でも重要な部分群です.

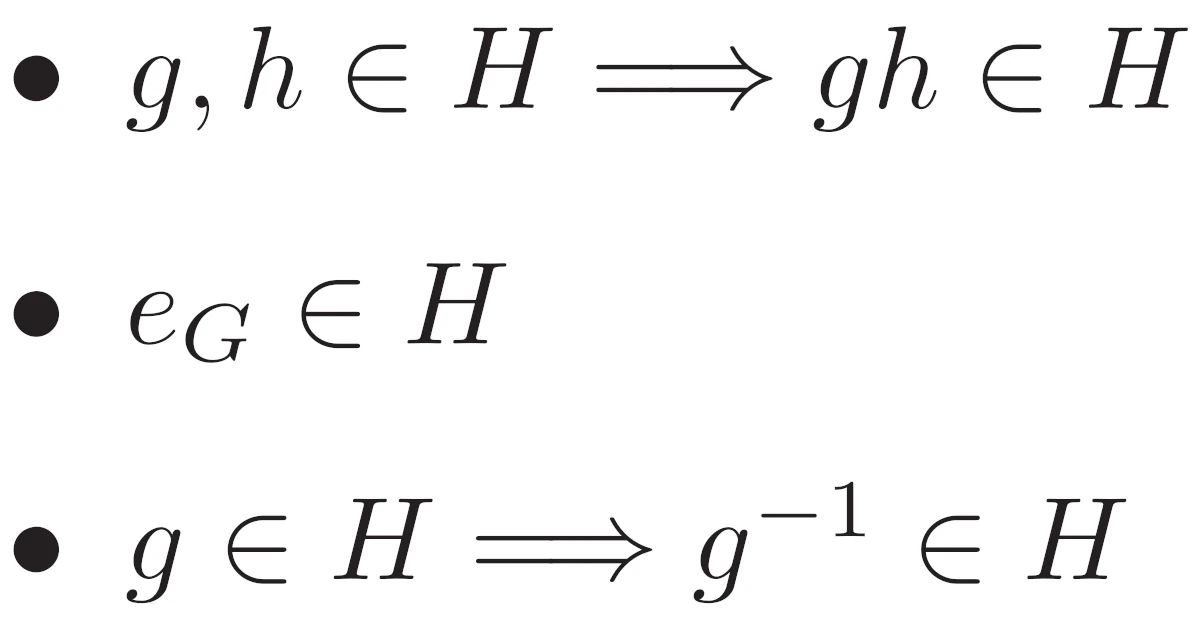
コメント