複素解析にはさまざまな綺麗な定理がありますが,その中でもシンプルで強力な定理としてコーシーの積分定理(Cauchy’s integral theorem)が挙げられます.
大雑把に言えば,このコーシーの積分定理は「正則関数の閉曲線上の複素積分は0である」という定理で,積分経路がどんなにグニャグニャしてようと閉でさえあれば正則関数の複素積分は必ず0になります.
この記事では
- コーシーの積分定理
- コーシーの積分定理の応用
- コーシーの積分定理の証明
を説明します.
「複素解析の基本」の一連の記事
コーシーの積分定理
まずはコーシーの積分定理を紹介し,具体例を紹介します.
定理
コーシーの積分定理は正則関数の複素積分に関する定理で次のとおりです.
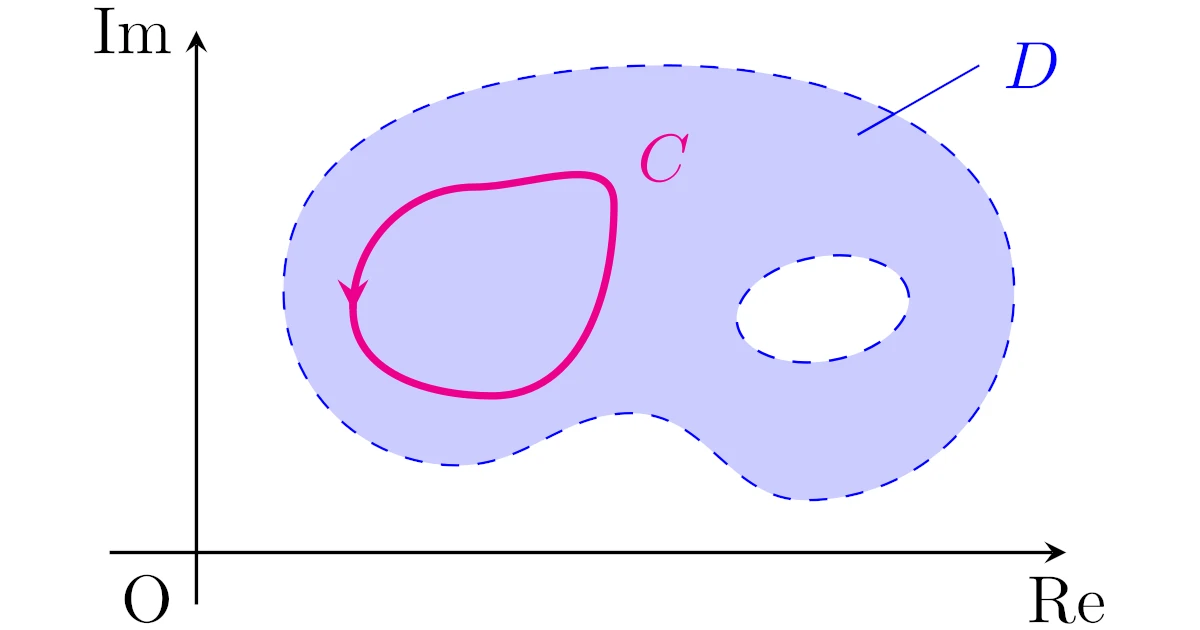
[コーシーの積分定理]領域$D$上の正則関数$f$を考える.複素平面上の有限の長さの閉曲線$C$の周および内部が$D$に含まれるとき,
\begin{align*}\int_{C}f(z)\,dz=0\end{align*}
が成り立つ.
領域$D$上の複素関数$f$が$D$上の全ての点で微分可能であるとき,$f$は$D$上の正則関数というのでした.
注意したいことは閉曲線$C$上だけではなく,$C$の内部でも微分可能でなければならないことです.
そのため,上図の領域$D$の右側に正則でない「穴」の部分がありますが,閉曲線$C$がこの「穴」の部分を囲っているような状況ではコーシーの積分定理は使えません.
具体例
次の問題はコーシーの積分定理から瞬時に解けます.
$z^n$は$\C$上で正則であり,$C$は長さ有限の閉曲線だから,コーシーの積分定理より
\begin{align*}\int_{C}z^n\,dz=0\end{align*}
である.
この問題では積分経路$C$はグニャグニャ曲がったり尖ったりしていても,閉曲線でさえあれば常にこの結果となります.
複素積分の記事では$C$が原点中心の円の場合で0となることを計算しましたが,コーシーの積分定理を使えば計算するまでもなく0と分かりますね.
コーシーの積分定理の応用(積分経路の変形)
コーシーの積分定理を用いると,複素積分の積分経路を変形することができます.
$C$を0を内部に含む複素平面上の長さ有限の任意の閉曲線とする.このとき,複素積分
\begin{align*}\int_{C}\frac{1}{z}\,dz\end{align*}
を求めよ.ただし,$C$には正の向きがついているとする.
$\frac{1}{z}$は$z=0$で微分不可能なので,この問題の複素積分の値をコーシーの積分定理から直接積分の値を求めることはできません.
しかし,コーシーの積分定理を用いると積分経路$C$を変形することができ,このことから積分の値を計算することができます.
閉曲線$C$の内部に含まれる原点中心・半径$R$の円周$C’$(正向き)を考える.
また,閉曲線$C$と円周$C’$を線分$\ell$で結び,$C$から$C’$に向かう向きを付ける.
一般に積分経路の始点と終点を繋げてよいから,
\begin{align*}&\int_{C}\frac{1}{z}\,dz-\int_{C’}\frac{1}{z}\,dz
\\=&\int_{C}\frac{1}{z}\,dz+\int_{\ell}\frac{1}{z}\,dz+\int_{-C’}\frac{1}{z}\,dz+\int_{-\ell}\frac{1}{z}\,dz
\\=&\int_{C\cup\ell\cup(-C’)\cup(-\ell)}\frac{1}{z}\,dz\quad\dots(*)\end{align*}
となる.曲線$C\cup\ell\cup(-C’)\cup(-\ell)$は閉曲線であり,この閉曲線の内部で$\frac{1}{z}$は正則関数である.
よって,コーシーの積分定理より$(*)=0$なので
\begin{align*}\int_{C}\frac{1}{z}\,dz=\int_{C’}\frac{1}{z}\,dz\end{align*}
となる.よって,$z\in C’$は$z=R(\cos{\theta}+i\sin{\theta})$($0\le\theta\le2\pi$)とおけるから
\begin{align*}\int_{C’}\frac{1}{z}\,dz
&=\int_{C’}\frac{\overline{z}}{|z|^{2}}\,dz
=\frac{1}{R^{2}}\int_{C’}\overline{z}\,dz
\\&=\frac{1}{R^{2}}\int_{0}^{2\pi}R(\cos{t}-i\sin{t})\cdot R(-\sin{t}+i\cos{t})\,dt
\\&=\int_{0}^{2\pi}i(\cos^{2}{t}+\sin^{2}{t})\,dt
=\int_{0}^{2\pi}i\,dt=2\pi i\end{align*}
となり,$\dint_{C}\dfrac{1}{z}\,dz=2\pi i$を得る.
この解答のように,閉積分経路$C$を微分不可能な点を「通過しない」ように動かす限りは複素積分の値が変わらないことが,コーシーの積分定理から正当化されるわけですね.
コーシーの積分定理の証明
それではコーシーの積分定理の証明に移りましょう.ここでは
- $C$が三角形の場合
- $C$が閉折れ線の場合
- $C$が一般の閉曲線の場合
を順に示します.
証明自体はテクニカルな部分もあるので,難しそうなら一旦飛ばしても問題ありません.
ステップ1($C$が三角形の場合)
$C$を三角形とし,任意の$\epsilon>0$をとる.$\abs{\dint_{C}f(z)\,dz}<\epsilon$を示せば良い.
$C$の各辺の中点を結ぶことにより$C$を4つの小三角形$C_i$($i=1,2,3,4$)に分割する.ただし,小三角形$C_i$の向きは$C$の向きに合うようにとる.
このとき,中点を結んだ部分の積分は打ち消し合うので,
\begin{align*}\int_{C}f(z)\,dz=\sum_{i=1}^{4}\int_{C_i}f(z)\,dz\end{align*}
が成り立つ.4つの$\abs{\int_{C_i}f(z)\,dz}$ ($i=1,2,3,4$)のうち最大の積分の積分経路の三角形を$C^{(1)}$とすると,三角不等式と併せて
\begin{align*}\abs{\int_{C}f(z)\,dz}
\le\sum_{i=1}^{4}\abs{\int_{C_i}f(z)\,dz}
\le4\abs{\int_{C^{(1)}}f(z)\,dz}\quad\dots(*)\end{align*}
が成り立つ.同様に$C^{(2)},C^{(3)},\dots$を順次定める.
このとき,$(*)$と同様の評価を繰り返せば,任意の自然数$n\in\N$に対して,
\begin{align*}\abs{\int_{C}f(z)\,dz}
\le&4\abs{\int_{C^{(1)}}f(z)\,dz}
\le4^2\abs{\int_{C^{(2)}}f(z)\,dz}
\\\le&\dots
\le4^n\abs{\int_{C^{(n)}}f(z)\,dz}\end{align*}
が成り立つ(厳密には帰納法).
また,$n\to\infty$で$C^{(n)}$全体はある一点$\alpha$に近付く.$\alpha$は$C$の周または内部の点だから,定理の仮定より$f$は$\alpha$で微分可能なので
\begin{align*}f'(\alpha)=\lim_{z\to\alpha}\frac{f(z)-f(\alpha)}{z-\alpha}\end{align*}
が存在する.よって,領域$D$に含まれる$\alpha$の近傍で複素関数$g$を$g(z):=\frac{f(z)-f(\alpha)}{z-\alpha}-f'(\alpha)$で定めると,$\lim_{z\to\alpha}g(z)=0$を満たす.すなわち,ある$\delta>0$が存在し,
\begin{align*}|z-\alpha|<\delta
\Ra&|g(z)|<\frac{\epsilon}{L^2}\end{align*}
が成り立つ.ただし,$L$は三角形$C$の周の長さである.
また,$n\to\infty$で$C^{(n)}$全体が$\alpha$に近付くことから,ある$N\in\N$が存在して,任意の$z\in C^{(N)}$に対して$|z-\alpha|<\delta$が成り立つ.
ここで,
\begin{align*}\int_{C^{(N)}}f(z)\,dz
=&\int_{C^{(N)}}\bra{f(\alpha)+g(z)(z-\alpha)+f'(\alpha)(z-\alpha)}\,dz
\\=&\int_{C^{(N)}}g(z)(z-\alpha)\,dz\end{align*}
となる.ここで$\int_{C^{(N)}}\,dz=\int_{C^{(N)}}z\,dz=0$であることを用いた(詳しくは前回の記事を参照).
絶対値は積分の中にある方が大きいか等しい(三角不等式)ことを併せて
\begin{align*}\abs{\int_{C^{(N)}}f(z)\,dz}
\le&\int_{C^{(N)}}|g(z)(z-\alpha)|\,|dz|
\\<&\frac{\epsilon}{L^2}\int_{C^{(N)}}|z-\alpha|\,|dz|\end{align*}
を得る.
また,三角形$C$の周の長さを$L$としていたから,三角形$C^{(N)}$の周の長さは$\frac{L}{2^N}$である.よって,任意の$z\in C^{(N)}$に対して$|z-\alpha|<\frac{L}{2^N}$となる.
以上を併せて,
\begin{align*}\abs{\int_{C}f(z)\,dz}
\le&4^N\abs{\int_{C^{(N)}}f(z)\,dz}
<\frac{4^N \epsilon}{L^2}\int_{C^{(N)}}\frac{L}{2^N}\,|dz|
\\=&\frac{4^N \epsilon}{L^2}\epsilon\bra{\frac{L}{2^N}}^2
=\epsilon\end{align*}
が従う.
ステップ2($C$が閉折れ線の場合)
$C$を三角形に分解して,ステップ1の「$C$が三角形の場合」を用いることで証明します.
$C$が閉折れ線とする.
このとき,$C$はいくつかの閉角形$C_1,\dots,C_n$に分割でき,
\begin{align*}\int_{C}f(z)\,dz=\sum_{k=1}^{n}\int_{C_k}f(z)\,dz\end{align*}
が成り立つ.
さらに,各多角形$C_i$ ($i=1,\dots,n$)はいくつかの三角形$C_{i,1},\dots,C_{i,m_i}$に分割でき,ステップ1を用いれば
\begin{align*}\int_{C}f(z)\,dz
=&\sum_{k=1}^{n}\sum_{\ell=1}^{m_i}\int_{C_{k,\ell}}f(z)\,dz
\\=&\sum_{k=1}^{n}\sum_{\ell=1}^{m_i}0=0\end{align*}
が従う.
ステップ3($C$が一般の閉曲線の場合)
$C$を閉折れ線で近似して,ステップ2の「$C$が閉折れ線の場合」を用いることで証明します.
$C$を一般の閉曲線とし,任意の$\epsilon>0$をとる.$\abs{\dint_{C}f(z)\,dz}<\epsilon$を示せば良い.
$D$は領域(開集合)で$C$は$D$の内部にある有限の長さの曲線だから,ある$r>0$が存在して,有界閉集合
\begin{align*}B:=B_r(C)=\set{z\in\C}{\exists w\in C\ \mathrm{s.t.}\ |z-w|\le r}\end{align*}
は$D$に含まれる.
$f$は$B$上で連続だから,$B$が有界閉集合であることより一様連続である(一般に有界閉集合$E$上で連続な複素関数$g$は$E$上一様連続).よって,ある$\delta>0$が存在して,$|z-w|<\delta$なる任意の$z,w\in B$に対して
\begin{align*}|f(z)-f(w)|<\frac{\epsilon}{2L}\end{align*}
が成り立つ.ただし,$L$は閉曲線$C$の周の長さである.
ここで,閉曲線$C$上の分点$z_0,z_1,\dots,z_n\in C$ ($z_0=z_n$)を順に「閉曲線$C$の$z_i$と$z_{i-1}$の間の部分$C_i$の長さが$\min\{\frac{\delta}{2},r\}$未満」を満たすようにとる.このとき,さらに複素積分の定義から
\begin{align*}\abs{\int_{C}f(z)\,dz-\sum_{i=1}^{n}f(\xi_i)(z_i-z_{i-1})}<\frac{\epsilon}{2}\end{align*}
となる$\xi_{i}\in C_i$ ($i=1,\dots,n$)が存在するようにできる.
また,線分$\overline{z_iz_{i-1}}$を$\ell_i$とし,$\ell_i$を繋いでできる閉折れ線を$\ell$とする.ただし,各$\ell_i$は$C_i$と同じ向きが付いているものとする.
このとき,各$C_i$の長さが$r$未満だから各$\ell_i$の長さも$r$未満なので$\ell\subset B$である.よって,
- ステップ2の結果
- 三角不等式
を用いると
\begin{align*}\abs{\int_{C}f(z)\,dz}
=&\abs{\int_{C}f(z)\,dz-\int_{\ell}f(z)\,dz}
\\\le&\abs{\int_{C}f(z)\,dz-\sum_{i=1}^{n}f(\xi_i)(z_i-z_{i-1})}
\\&\quad+\abs{\sum_{i=1}^{n}f(\xi_i)(z_i-z_{i-1})-\int_{\ell}f(z)\,dz}
\\<&\frac{\epsilon}{2}+\sum_{i=1}^{n}\abs{f(\xi_i)(z_i-z_{i-1})-\int_{\ell_i}f(z)\,dz}\end{align*}
が成り立つ.さらに
- $\ell_i$上の任意の点$z$と$\xi_i$に対して$|\xi_i-z|<\delta$
- $\ell$の長さは$C$の長さ$L$以下
を用いると,
\begin{align*}&\sum_{i=1}^{n}\abs{f(\xi_i)(z_i-z_{i-1})-\int_{\ell_i}f(z)\,dz}
\\=&\sum_{i=1}^{n}\abs{\int_{\ell_i}(f(\xi_i)-f(z))\,dz}
\le\sum_{i=1}^{n}\int_{\ell_i}|f(\xi_i)-f(z)|\,|dz|
\\<&\sum_{i=1}^{n}\int_{\ell_i}\frac{\epsilon}{2L}\,|dz|
\le L\cdot\frac{\epsilon}{2L}
=\frac{\epsilon}{2}\end{align*}
が成り立つ.以上より$\abs{\dint_{C}f(z)\,dz}<\epsilon$を得る.


コメント