ディリクレ積分を複素積分で計算する｜sin(x)/xの広義積分

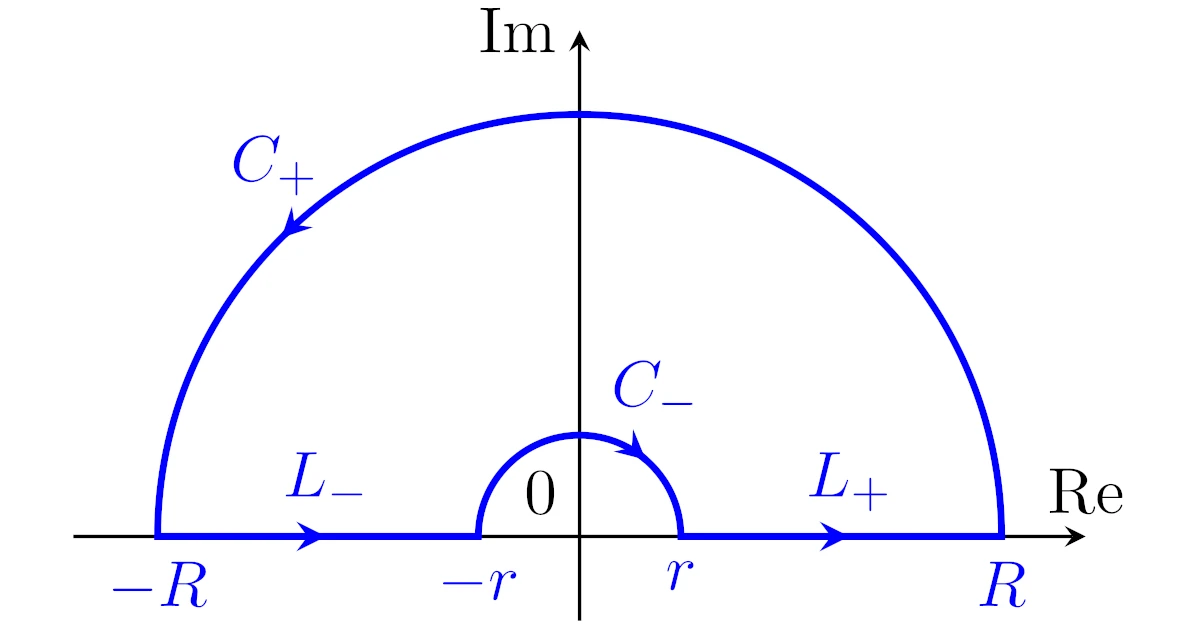
複素関数$f(z)=\dfrac{e^{iz}}{z}$とおく．また，複素平面上の４つの経路

• $L_+:=\set{z\in\C}{z=x,x\in[r,R]}$
• $L_-:=\set{z\in\C}{z=x-(r+R),x\in[r,R]}$
• $C_+:=\set{z\in\C}{z=Re^{i\theta},\theta\in[0,\pi]}$
• $C_-:=\set{z\in\C}{z=re^{i(\pi-\theta)},\theta\in[0,\pi]}$

をとる．ただし，$0<r<R$である．

このとき，$f$は$L_{\pm}$, $C_{\pm}$を繋いでできる経路の周および内部で正則なので，コーシーの積分定理より

\begin{align*}0=\bra{\int_{L_+}+\int_{L_-}+\int_{C_+}+\int_{C_-}}f(z)\,dz\quad\dots(*)\end{align*}

が成り立つ．以下，４ステップに分けて示す．

ステップ１（$L_{\pm}$上の積分とディリクレ積分）

ディリクレ積分は

\begin{align*}\int_{0}^{\infty}\frac{\sin{x}}{x}\,dx
&=\lim_{\substack{r\to+0\\R\to\infty}}\int_{r}^{R}\frac{\sin{x}}{x}\,dx
\\&=\lim_{\substack{r\to+0\\R\to\infty}}\operatorname{Im}\int_{L_+}f(z)\,dz\end{align*}

である．また，変数変換$x=-y$により

\begin{align*}&\int_{L_-}f(z)\,dz
=\int_{-R}^{-r}\frac{\sin{x}}{x}\,dx
\\&=\int_{R}^{r}\frac{\sin{(-y)}}{-y}\,(-dy)
=\int_{r}^{R}\frac{\sin{y}}{y}\,dy
\\&=\int_{L_+}f(z)\,dz
\end{align*}

である．よって，$(*)$と併せてディリクレ積分は

\begin{align*}&\int_{0}^{\infty}\frac{\sin{x}}{x}\,dx
\\&=\frac{1}{2}\lim_{\substack{r\to+0\\R\to\infty}}\operatorname{Im}\bra{\int_{L_+}+\int_{L_-}}f(z)\,dz
\\&=-\frac{1}{2}\lim_{\substack{r\to+0\\R\to\infty}}\operatorname{Im}\bra{\int_{C_+}+\int_{C_-}}f(z)\,dz\end{align*}

となる．

ステップ２（$C_+$上の積分）

$C_+$上で$\dfrac{dz}{d\theta}=iRe^{i\theta}$なので，

\begin{align*}\int_{C_{+}}f(z)\,dz
&=\int_{0}^{\pi}\frac{e^{iRe^{i\theta}}}{Re^{i\theta}}\cdot iRe^{i\theta}\,d\theta
\\&=i\int_{0}^{\pi}e^{R(i\cos{\theta}-\sin{\theta})}\,d\theta\end{align*}

である．三角不等式と$|e^{i\cos{\theta}}|=1$を併せて

\begin{align*}\abs{\int_{C_{+}}f(z)\,dz}
&\le\int_{0}^{\pi}e^{-R\sin{\theta}}\,d\theta
=2\int_{0}^{\frac{\pi}{2}}e^{-R\sin{\theta}}\,d\theta
\\&\le2\int_{0}^{\frac{\pi}{2}}e^{-\frac{2R}{\pi}\theta}\,d\theta
=-\frac{\pi}{R}\brc{e^{-\frac{2R}{\pi}\theta}}_{0}^{\frac{\pi}{2}}
\\&=-\frac{\pi}{R}(1-e^{-R})
\xrightarrow[]{R\to\infty}0\end{align*}

が成り立つ．ただし，

• １つ目の等号では$y=\sin{\theta}$が$\theta=\dfrac{\pi}{2}$に関して対称

  

• ２つ目の不等号では任意の$\theta\in[0,\frac{\pi}{2}]$に対して$\dfrac{2}{\pi}\theta\le\sin{\theta}$

  

であることを用いた．よって，$\lim\limits_{R\to\infty}\dint_{C_{+}}f(z)\,dz=0$を得る．

ステップ３（$C_-$上の積分）

$e^{iz}$は$\C$上で

\begin{align*}e^{iz}
&=\frac{1}{0!}+\frac{iz}{1!}+\frac{(iz)^2}{2!}+\frac{(iz)^3}{3!}+\dots
\\&=1+iz-\frac{z^2}{2!}-\frac{iz^3}{3!}+\dots\end{align*}

とテイラー展開でき，この収束半径は$\infty$である．よって，$f$は原点の除外近傍上で

\begin{align*}f(z)=\frac{1}{z}+i-\frac{z}{2!}-\frac{iz^2}{3!}+\dots\end{align*}

とローラン展開でき，

\begin{align*}\int_{C_{-}}f(z)\,dz=\sum_{n=0}^{\infty}\frac{i^n}{n!}\int_{C_{-}}z^{n-1}\,dz\end{align*}

と項別積分可能である．ここで，$I_n:=\dint_{C_{-}}z^{n-1}\,dz$とおく．

$C_-$上で$\dfrac{dz}{d\theta}=-ire^{i(\pi-\theta)}$なので，$n\ge1$なら

\begin{align*}I_n
&=\int_{0}^{\pi}(re^{i(\pi-\theta)})^{n-1}(-ire^{i(\pi-\theta)})\,d\theta
\\&=-ir^ne^{in\pi}\int_{0}^{\pi}e^{-in\theta}\,d\theta
\\&=\frac{r^ne^{in\pi}}{n}\bra{(-1)^n-1}
\xrightarrow[]{r\to+0}0\end{align*}

となり，$n=0$なら

\begin{align*}I_0
&=\int_{0}^{\pi}(re^{i(\pi-\theta)})^{-1}(-ire^{i(\pi-\theta)}\,d\theta)
\\&=-i\int_{0}^{\pi}\,d\theta
=-\pi i\end{align*}

となる．よって，$\lim\limits_{r\to+0}\dint_{C_{-}}f(z)\,dz=-\pi i$を得る．

ステップ４（ディリクレ積分を求める）

ステップ１〜ステップ３を併せて

\begin{align*}&\int_{0}^{\infty}\frac{\sin{x}}{x}\,dx
\\&=-\frac{1}{2}\operatorname{Im}\bra{\lim_{R\to\infty}\int_{C_+}f(z)\,dz+\lim_{r\to+0}\int_{C_-}f(z)\,dz}
\\&=-\frac{1}{2}\operatorname{Im}(0-\pi i)
=-\frac{1}{2}\cdot(-\pi)
=\frac{\pi}{2}\end{align*}

を得る．