作用素の中でも有界作用素は様々な良い性質をもちます.
リース-トーリン(リース-ソリン,Riesz-Thorin)の複素補間定理(または単にリースの補間定理)は1つの有界作用素が2つの$L^pL^q$有界性を持つとき「その間の有界性」を保証する定理の1つで,簡単には次のように述べられます.
線形作用素$T$が$L^{p_0}\to L^{q_0}$と$L^{p_1}to L^{q_1}$の有界性をもつとき,任意の$\theta\in(0,1)$に対して
\begin{align*}p_{\theta}:=\bra{\frac{1-\theta}{p_0}+\frac{\theta}{p_1}}^{-1},\quad
q_{\theta}:=\bra{\frac{1-\theta}{q_0}+\frac{\theta}{q_1}}^{-1}\end{align*}
とすると$T$は$L^{p_{\theta}}\to L^{q_{\theta}}$の有界性をもつ.
座標平面上の点$(1/p_{\theta},1/q_{\theta})$は2点$(1/p_0,1/q_0)$, $(1/p_1,1/q_1)$を結ぶ線分の内分点となりますね.
つまり,ある2点$(1/p,1/q)=(1/p_0,1/q_0),(1/p_1,1/q_1)$で作用素$T$が$L^pL^q$の有界性があれば,この2点を結ぶ線分上の任意の点$(1/p,1/q)=(1/p’,1/q’)$に対しても$T$は$L^{p’}L^{q’}$の有界性をもつというわけですね.
2つの状況で成り立っており,それらのある意味での「間」の場合にも成り立つことを保証する定理を一般に補間定理といいます(「補完」ではないことに注意).
この記事では
- アダマールの三線定理
- リース-トーリンの複素補間定理
を順に解説します.
アダマールの三線定理
リース-トーリンの複素補間定理の証明のために,アダマール(Hadamard)の三線定理を証明します.
アダマールの三線定理はフラグメン-リンデレフ(Phragmén-Lindelöf)の原理をもとにしているため,アダマール-フラグメン-リンデレフの三線定理と呼ぶこともあるようです.
[アダマールの三線定理]閉集合$S\subset\C$を
\begin{align*}S:=\set{x+iy\in\C}{x\in[0,1],y\in\R}\end{align*}
で定め,複素関数$F:S\to\C$は$S$で連続かつ有界で,$S$の内部$S^\circ$で正則であるとする.$M_0,M_1>0$が
\begin{align*}\sup_{y\in\R}|F(iy)|\le M_0,\quad
\sup_{y\in\R}|F(1+iy)|\le M_1\end{align*}
を満たすとすると,任意の$z=x+iy\in S^{\circ}$に対して$|F(z)|\le M_0^{1-x}M_1^{x}$が成り立つ.
関数$G,G_n:S\to\C$を
\begin{align*}G(z):=\frac{F(z)}{M_0^{1-z}M_1^{z}},\quad
G_n(z):=G(z)e^{(z^2-1)/n}\end{align*}
で定める($n\in\N$).以下のことに注意しておく:
- 任意の$z=x+iy\in S$に対して,$0\le x\le1$だから\begin{align*}|e^{(z^2-1)/n}|=|e^{(x^2+ixy-y^2-1)/n}|\le e^{-y^2/n}\le1.\end{align*}
- 任意の$z=x+iy\in S$に対して,\begin{align*}|M_0^{1-z}M_1^{z}|=|M_0^{(1-x)-iy}||M_1^{x+iy}|=M_0^{1-x}M_1^{x}.\end{align*}
十分遠方で$|G_n(z)|\le1$が成り立つことの証明
$G$は有界なので,ある$M>0$が存在して,任意の$z\in S$に対して$|G(z)|\le M$が成り立つ.よって,
\begin{align*}\sup_{\substack{n\in\N\\x\in[0,1]}}|G_n(z)|&=\sup_{\substack{n\in\N\\x\in[0,1]}}|G(z)e^{(z^2-1)/n}|
\\&\le\sup_{\substack{n\in\N\\x\in[0,1]}}|G(z)|e^{-y^2/n}
\\&\le Me^{-y^2}\xrightarrow[]{|y|\to\infty}0\end{align*}
が成り立つ.すなわち,$n$と$x$によらない$R>0$が存在して,$|y|\ge R$なら$|G_n(x+iy)|\le1$が成り立つ.
とくに$n$によらず$|\operatorname{Im}z|=R$なら$|G_n(z)|\le1$が成り立つ.
境界$\partial S$上で$|G_n(z)|\le1$が成り立つことの証明
任意の$z=x+iy\in S$に対して,
\begin{align*}|G_n(z)|\le|G(z)|=\frac{|F(z)|}{|M_0^{1-z}M_1^{z}|}=\frac{|F(z)|}{M_0^{1-x}M_1^{x}}\end{align*}
である.よって,任意の$y\in\R$に対して
\begin{align*}&|G_n(iy)|\le\frac{|F(iy)|}{M_0}\le1,\quad
\\&|G_n(1+iy)|\le\frac{|F(1+iy)|}{M_1}\le1\end{align*}
が成り立つ.
$S$上で$|F(z)|\le M_0^{1-x}M_1^{x}$が成り立つことの証明
上で示したことから,$S$の有界部分集合
\begin{align*}S’:=\set{z\in S}{|\operatorname{Im}z|\le R}\end{align*}
の境界$\partial S’$上で$|G_n|$は1以下の値をとる.$G_n$は$S’$で連続で,$S’$の内部$\partial S’$で正則だから,最大絶対値の原理と併せて
\begin{align*}\sup_{z\in S’}|G_n(z)|\le\sup_{z\in\partial S’}|G_n(z)|\le1\end{align*}
が成り立つ.さらに,$|z|\ge R$なら$|G_n(z)|\le1$であることも併せれば,任意の$z\in S$に対して
\begin{align*}|G(z)|=\lim\limits_{n\to\infty}|G_n(z)|\le1\end{align*}
が従う.$|G(z)|=\dfrac{|F(z)|}{M_0^{1-x}M_1^{x}}$だから,
\begin{align*}|F(z)|\le M_0^{1-x}M_1^{x}\end{align*}
が従う.
リース-トーリンの複素補間定理
アダマールの三線定理を用いて,次のリース-トーリンの複素補間定理を示します.
[リース-トーリンの複素補間定理]$(X,\mathcal{A},\mu)$, $(Y,\mathcal{B},\nu)$を測度空間とし,$p_0,q_0,p_1,q_1\ge1$は$p_0\neq p_1$, $q_0\neq q_1$を満たすとする.$X$上の可測関数から$Y$上の可測関数への線形作用素$T$は
- $L^{p_0}(X)\to L^{q_0}(Y)$として有界で,$\|T\|_{L^{p_0}(X)\to L^{q_0}(Y)}=M_0$
- $L^{p_1}(X)\to L^{q_1}(Y)$として有界で,$\|T\|_{L^{p_1}(X)\to L^{q_1}(Y)}=M_1$
を満たすとする.このとき,任意の$\theta\in(0,1)$に対して,$p_{\theta}$, $q_{\theta}$を
\begin{align*}p_{\theta}:=\bra{\frac{1-\theta}{p_0}+\frac{\theta}{p_1}}^{-1},\quad
q_{\theta}:=\bra{\frac{1-\theta}{q_0}+\frac{\theta}{q_1}}^{-1}\end{align*}
と定めると,$T$は$L^{p_{\theta}}(X)$から$L^{q_{\theta}}(Y)$への有界作用素で,このときの作用素ノルム$M_{\theta}$は$M_0^{1-\theta}M_1^{\theta}$以下である.
ただし,ここでの$X$, $Y$上の関数は全て複素数値である.
一般の測度空間$X$, $Y$に対して成り立つので,$X=Y=\R^n$のルベーグ空間でも問題なく成り立ちます.
$r\in\C\setminus\{0\}$に対して,$r’:=(1-\frac{1}{r})^{-1}$とする.また,集合$S\subset\C$を
\begin{align*}S:=\{z\in\C|\operatorname{Re}z\in[0,1]\}\end{align*}
で定める(三線定理での集合$S$と同じもの).
単関数近似と証明の方針
$X$, $Y$上可積分な単関数全部の部分空間をそれぞれ$\text{Simp}(X)$, $\text{Simp}(Y)$とすると,任意の$p,q\in[0,1)$に対して$\text{Simp}(X)$, $\text{Simp}(Y)$はそれぞれ$L^{p}(X)$, $L^{q}(Y)$で稠密である.
よって,任意の$f\in\text{Simp}(X)$, $g\in\text{Simp}(Y)$に対して
\begin{align*}\sup_{\substack{f\in\text{Simp}(X)\\ \|f\|_{p_{\theta}}=1}}\Biggl(\sup_{\substack{g\in\text{Simp}(Y)\\ \|g\|_{q_{\theta}’}=1}}|\anb{Tf,g}|\Biggr)\le M_0^{1-\theta}M_1^{\theta}\end{align*}
が成り立つことを示せば,
\begin{align*}\sup_{\substack{f\in L^{p_{\theta}}(X)\\ \|f\|_{p_{\theta}}=1}}\Biggl(\sup_{\substack{g\in L^{q_{\theta}’}(X)\\ \|g\|_{q_{\theta}’}=1}}|\anb{Tf,g}|\Biggr)\le M_0^{1-\theta}M_1^{\theta}\end{align*}
が成り立つので,作用素ノルムの定義と$L^{q_{\theta}}$の双対性を併せて,
\begin{align*}\|T\|_{L^{p_{\theta}}(X)\to L^{q_{\theta}}(Y)}
&=\sup_{\substack{f\in L^{p_{\theta}}(X)\\ \|f\|_{p_{\theta}}=1}}\|Tf\|_{q_{\theta}}
\\&=\sup_{\substack{f\in L^{p_{\theta}}(X)\\ \|f\|_{p_{\theta}}=1}}\Biggl(\sup_{\substack{g\in L^{q_{\theta}’}(X)\\ \|g\|_{q_{\theta}’}=1}}|\anb{Tf,g}|\Biggr)
\\&\le M_0^{1-\theta}M_1^{\theta}\end{align*}
が従う.
単関数$f$, $g$と複素関数$\phi$, $\psi$, $F$の準備
[単関数$f$, $g$の定義]$\|f\|_{p_{\theta}}=\|g\|_{q_{\theta}’}=1$なる$f\in\text{Simp}(X)$, $g\in\text{Simp}(Y)$を任意にとり,それぞれ
\begin{align*}f=\sum_{k=1}^{n} a_k\mathbb{I}_{X_k},\quad g=\sum_{\ell=1}^{m} b_\ell\mathbb{I}_{Y_\ell}\end{align*}
と表す.ただし,
- $a_1,a_2,\dots,a_n,b_1,b_2,\dots,b_m\in\C$
- $X_1,X_2,\dots,X_n$は互いに素で$X=X_1\cup X_2\cup\dots\cup X_n$
- $Y_1,Y_2,\dots,Y_m$は互いに素で$Y=Y_1\cup Y_2\cup\dots\cup Y_m$
である.
[関数$\phi$, $\psi$, $F$の定義]$z\in S$に対して,$p_{z}$, $q_{z}$を
\begin{align*}p_{z}:=\bra{\frac{1-z}{p_0}+\frac{z}{p_1}}^{-1},\quad
q_{z}:=\bra{\frac{1-z}{q_0}+\frac{z}{q_1}}^{-1}\end{align*}
で定め,複素関数$\phi;X\times S\to\C$, $\psi:Y\times S\to\C$をそれぞれ
\begin{align*}&\phi(x,z):=\sum_{k=1}^{n}|a_k|^{p_{\theta}/p_{z}}e^{i\arg{a_k}}\mathbb{I}_{X_k}(x),
\\&\psi(y,z):=\sum_{\ell=1}^{m}|b_\ell|^{q_{\theta}’/q_{z}’}e^{i\arg{b_\ell}}\mathbb{I}_{Y_\ell}(y)\end{align*}
で定める.さらに,複素$F:S\to\C$を
\begin{align*}F(z):=\anb{T(\phi(\cdot,z)),\psi(\cdot,z)}=\int_{Y}T(\phi(\cdot,z))(y)\psi(y,z)\,dy\end{align*}
で定める.
複素関数$\phi$, $\psi$のノルム
一般に集合$A$, $B$が互いに素なら,任意の$a,b,w\in\C$に対して$|a\mathbb{I}_{A}+b\mathbb{I}_{B}|^{w}=|a|^w\mathbb{I}_{A}+|b|^w\mathbb{I}_{B}$を満たすことに注意する.
いま$X_1,X_2,\dots,X_n$は互いに素だから,
\begin{align*}\phi(x,z)&=\sum_{k=1}^{n}|a_k|^{p_{\theta}(\frac{1-z}{p_0}+\frac{z}{p_1})}\mathbb{I}_{X_k}(x)
\\&=|f(x)|^{p_{\theta}(\frac{1-z}{p_0}+\frac{z}{p_1})}\end{align*}
となり,
\begin{align*}|\phi(x,z)|&=\abs{|f(x)|^{p_{\theta}(\frac{1-z}{p_0}+\frac{z}{p_1})}}
\\&=|f(x)|^{p_{\theta}(\frac{1-x}{p_0}+\frac{x}{p_1})}\end{align*}
である.$\|f\|_{p_{\theta}}=1$より$\int_{X}|f(x)|^{p_{\theta}}\,dx=1$だから
\begin{align*}\int_{X}|\phi(x,iy)|^{p_0}\,dx&=\int_{X}\bra{|f(x)|^{p_{\theta}(\frac{1-0}{p_0}+\frac{0}{p_1})}}^{p_0}\,dx
\\&=\int_{X}|f(x)|^{p_{\theta}}\,dx=1\end{align*}
なので,$\|\phi(\cdot,iy)\|_{p_0}=1$が成り立つ.同様に
\begin{align*}\|\psi(\cdot,iy)\|_{q_0′}=\int_{X}|f(x)|^{q_{\theta}’}\,dx=1\end{align*}
が成り立つ.
$\psi$についても同様に$\|\phi(\cdot,1+iy)\|_{p_1}=1$, $\|\psi(\cdot,1+iy)\|_{q_1′}=1$が成り立つ.
複素関数$F$の連続性・正則性・有界性
$T$と積分の線形性より,
\begin{align*}F(z):=\sum_{k,\ell}|a_k|^{p_{\theta}/p_{z}}|b_\ell|^{q_{\theta}’/q_{z}’}e^{i(\arg{a_k}+\arg{b_\ell})}\anb{T\mathbb{I}_{X_k},\mathbb{I}_{Y_\ell}}\end{align*}
であって,各$k,\ell$に対して
\begin{align*}&|a_k|^{p_{\theta}/p_{z}}=|a_k|^{p_{\theta}\bra{\frac{1-z}{p_0}+\frac{z}{p_1}}}, \\&|b_\ell|^{q_{\theta}’/q_{z}’}=|b_\ell|^{q_{\theta}’\bra{\frac{1-z}{q_0′}+\frac{z}{p_1′}}}\end{align*}
だから,$F$は実数倍の指数関数の線形結合である.よって,$F$は$S$上連続で,$S$の内部で正則である.
また,ヘルダーの不等式より
\begin{align*}|F(iy)|&\le\|T\phi(\cdot,iy)\|_{q_0}\|\psi(\cdot,iy)\|_{q_0′}
\\&\le M_0\|\phi(\cdot,iy)\|_{p_0}\|\psi(\cdot,iy)\|_{q_0′}=M_0,
\\|F(1+iy)|&\le\|T\phi(\cdot,1+iy)\|_{q_1}\|\psi(\cdot,1+iy)\|_{q_1′}
\\&\le M_1\|\phi(\cdot,1+iy)\|_{p_1}\|\psi(\cdot,1+iy)\|_{q_1′}=M_1\end{align*}
が成り立つ.
アダマールの三線定理の適用
任意の$z=x+iy\in S^{\circ}$に対して,
\begin{align*}|\anb{Tf,g}|
&=|\anb{T\phi(\cdot,\theta),\psi(\cdot,\theta)}|
\\&=|F(\theta)|\le M_0^{1-\theta}M_1^{\theta}\end{align*}
が従う.
よって,単関数近似から$\|f\|_{p_{\theta}}=\|g\|_{q_{\theta}’}=1$なる任意の$f\in L^{p_{\theta}},g\in L^{q_{\theta}’}$に対しても,$|\anb{Tf,g}|\le M_0^{1-\theta}M_1^{\theta}$が成り立つ.
したがって,
作用素ノルムの定義と$L^{q_{\theta}}$の双対性を併せて,
\begin{align*}\|T\|_{L^{p_{\theta}}(X)\to L^{q_{\theta}}(Y)}
&=\sup_{\substack{f\in L^{p_{\theta}}(X)\\ \|f\|_{p_{\theta}}=1}}\|Tf\|_{q_{\theta}}
\\&=\sup_{\substack{f\in L^{p_{\theta}}(X)\\ \|f\|_{p_{\theta}}=1}}\Biggl(\sup_{\substack{g\in L^{q_{\theta}’}(X)\\ \|g\|_{q_{\theta}’}=1}}|\anb{Tf,g}|\Biggr)
\\&\le M_0^{1-\theta}M_1^{\theta}\end{align*}
が従う.
リース-トーリンの補間定理を用いることで,自由シュレディンガー発展作用素の分散型評価($L^pL^q$評価)を証明することができます.
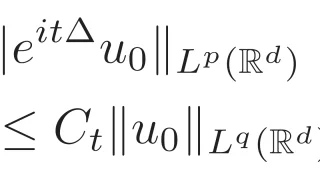
参考文献
以下は参考文献です.
非線形発展方程式の実解析的方法
[小川卓克 著/丸善出版(シュプリンガー現代数学シリーズ)]
本書は関数空間に関する予備知識をじっくりと準備し,
- 波動方程式
- 熱方程式
- Schrödinger方程式
- Navier-Stokes方程式
といった非線形発展方程式を考えていきます.
本書の特徴は,様々な非線形発展方程式を広く扱っている点と,証明へのアプローチを説明して直感的な理解を促している点です.
本書が全19章と多くの章から構成されていることからも,広くトピックを扱っていることが見てとれますね.
誤植が多いのがただ1つ残念な点ではありますが,これほどに広く丁寧に非線形発展方程式を扱っている和書は他に見当たらず,この分野の基礎や考え方をカバーするには良い教科書と言えます.
(追記)現在は絶版になっており,中古でしか入手できないようです.


コメント