私が高校で初めて積分を学んだとき「こんな曲がった境界をもつ図形の面積も求められるのか!」と衝撃を受けたことを今でも覚えています.
しかし,高校で学ぶ積分は少々大雑把で,厳密に定義される積分を学ぶには大学の微分積分学で学ぶリーマン積分まで待たなくてはなりません.
ただし,リーマン積分の考え方は直感的でシンプルですが,専門的に積分を扱おうとすると少々扱いづらいという欠点がありました.
そこで1900年頃に数学者のアンリ・ルベーグはリーマン積分とは異なる新たなアプローチで理論を再構築し,リーマン積分の欠点を大幅に改善する画期的な積分を考えました.現在ではこの積分はルベーグ積分とよばれています.
この記事では
- 積分の原型は土地の面積を測る方法
- 積分は図形と関数の関係から始まった
- リーマン積分は定義域に注目する積分
- ルベーグ積分は値域に注目する積分
- ルベーグ積分の良さ
を順に解説します.
「ルベーグ積分の基本」の一連の記事
- ルベーグ測度
- ルベーグ可測関数とルベーグ積分
積分の原型は土地の面積を測る方法
積分の原型が生まれたのは紀元前2000年頃の古代エジプトだったと言われてます.
アフリカ大陸には最高峰の標高が5000mを超えるルウェンゾリ山地があり,冬に降った雪が春になると溶けてナイル川に流れ込みます.
このとき膨大な量の水が流れ込むことでナイル川は毎年氾濫を起こしてしまうのですが,上流から流れてきた栄養豊富な土がその年の農作の糧となりエジプト文明を支えていました.このような背景から「エジプトはナイルの賜物」という言葉が生まれたほどです.
しかし,ナイル川が氾濫することで地形が変わってしまうので,新たに測量して土地を分割し直す必要があります.
ここで考えられた測量術は「三角形で少しずつ土地を覆い,三角形の面積の和で土地の面積を求める」という方法で,現在この方法は取り尽くし法などとよばれます.
「取り尽くし法」という言葉は当時の人々が使っていたわけではなく,使われ始めたのは15世紀半ば頃のようです.
三角形の面積は当時もよく知られていましたから,これで土地のおおよその面積が分かることになります.
ただ,もちろんこの有限個の三角形では曲がった境界を持つ領域を埋め尽くすことはできず,正確な面積を求めることはできません.
しかし,だいたいの土地の面積が求まれば十分だったからか,厳密に面積を考える理論はあまり考えられなかったようです.
このような「土地(geo)を測る(metry)こと」は「幾何学」を意味する“geometry”の語源にもなっています.
積分は図形と関数の関係から始まった
1600年代に入ると,面積を求めるための様々な道具が出揃い始めます.
関数と図形には密接な関係がある
1600年代前半の数学者(哲学者)ルネ・デカルト(René Descartes)は2つの数を「縦」と「横」の2方向で図示できることを思い付きました.これが中学校以来学んできた座標の始まりです.
大雑把に言えば関数とは「数を与えると数をただ1つ返す規則」のことで,座標により関数$f$に対して方程式$y=f(x)$を$xy$平面上にグラフとして図示できるようになり,関数が図形的にも理解できるようになります.
例えば$f(x)=x^2$で表される関数$f$は「数$x$を与えると$x^2$を返す規則」なわけですが,方程式$y=f(x)$が$xy$平面に放物線として図示できるのは皆さんよくご存知ですね.
このように座標を考えることで,図形と関数が密接な関係にあることが理解され始め,面積を求めるために関数が使われ始めます.
つまり,下図の水色領域の面積を知りたければ,このグラフを表す関数$f$を考察するとよいことになるわけですね.
そして,この領域の面積を
\begin{align*}\int_{a}^{b}f(x)\,dx\end{align*}
と表し,$\displaystyle\int$を伴う計算を一般に積分とよぶわけですね.
黎明期の積分
しかし,当時は積分を計算する一般的な方法が知られておらず,1つ1つの積分の計算は様々な工夫のもとに行われていました.
たとえば,デカルトの正葉線と呼ばれる
\begin{align*}x^{3}+y^{3}=axy\quad(a>0)\end{align*}
で表される$xy$平面上のグラフは以下のようになります.
この曲線で囲まれる領域の面積は今は高校生でも求められますが,当時は様々な工夫により計算されていたようです.
古典的な求積法については「古典的難問に学ぶ微分積分」(高瀬正仁著,共立出版)でいくつか紹介されています.高校数学の微分積分が理解できていれば読める内容となっており,数学好きの高校生〜大学1,2年生にオススメしたい好著です.
微分と積分はおおよそ逆の関係にある
中世のヨーロッパで積分を計算する一般的な方法が知られていなかったのは,まだ微分法の考え方が確立されていなかったのが大きな理由です.
高校数学を学んだ方には「歴史的には微分よりもずっと先に積分が考えられていて,数学的にも微分と積分はもともと全く別のもの」という事実には少し驚きがあるかも知れませんね.
現代では微分法は
- アイザック・ニュートン(Isaac Neton)
- ゴッドフリート・ライプニッツ(Gottfried Leibniz)
がそれぞれ独立に考え出したものとされていますが,当時2人は微分法がどちらの功績か20年にもわたって争ったと言われています.
現代でも広く使われている微分の記法$\dfrac{dy}{dx}$を考えたのはライプニッツで,この記法はとても便利で微分と積分の関係を見事に表現することができます.この意味でライプニッツの記法は微分積分学の発展に大きく貢献したといえます.
微分法が考え出されると「微分と積分はどうやら繋がっていて,連続関数のような性質の良い関数に対しては微分と積分はおおよそ逆の関係になっている」ということが分かってきます:
\begin{align*}&\od{}{x}\int_{a}^{x}f(t)\,dt=f(x),
\\&\int_{a}^{x}\od{f}{t}(t)\,dt=f(x)-f(a).\end{align*}
このことは今では微分積分学の基本定理とよばれています.
高校数学で「積分は微分の逆演算(微分してもとに戻る関数を求めるのが積分)」と学ぶのは,これは微分積分学の基本定理が背景にあるからなわけですね.
ともかく微分積分学の基本定理により積分の一般的な計算方法が考えられ,当時の数学者によって積分は微分と併せて大きく発展していくことになります.
リーマン積分は定義域に注目する積分
その後,数学界全体で数学をより厳密に整備し直すべきだという風潮が広まります.
リーマン積分は縦長の長方形で面積を考える
この風潮は積分に対しても例外ではありませんでした.1800年代になるとベルンハルト・リーマン(Bernhard Riemann)は積分の厳密な定義を与えました.
リーマンは$\displaystyle\int_{0}^{1}f(x)\,dx$を計算するには「$xy$平面上の$y=f(x)$のグラフと$x$軸で囲まれる$0\le x\le 1$の領域を縦長に細長く切り,長方形によって近似すればよい」と考えました.
この考え方による積分をリーマン積分といいます.
上図は分かりやすさのためスライスの幅が等しく長方形の縦の長さがスライスの左端の値になっていますが,本来のリーマン積分はスライスの幅がバラバラでもよく長方形の高さも左端の値でなくても構いません.
もちろん,この図のように「荒いスライス」では長方形で近似した面積(水色部分)と,もともと考えていた$\displaystyle\int_{0}^{1}f(x)\,dx$に差があります.
そこで,このスライスの幅をもっと細かくすると下図のようになります.
この図は先ほどよりも$\displaystyle\int_{0}^{1}f(x)\,dx$との誤差が小さくなっており,近似した長方形の面積はより$\displaystyle\int_{0}^{1}f(x)\,dx$に近付くことが見てとれます.
そこで,リーマン積分は「(スライスの最大幅)→0の極限により,いつでも長方形近似による面積が『同じ値』に収束するとき,リーマン積分可能であるといい,この極限を$\displaystyle\int_{0}^{1}f(x)\,dx$と表そう」と定義されます.
ディリクレ関数(リーマン積分不可能な関数)
しかし,実はリーマン積分では「長方形近似の高さ」を決める段階で問題が生じて,リーマン積分を考えられない関数もあります.
例えば,次で定まる関数$f$はディリクレ(Dirichlet)関数という名前がついています:
\begin{align*}f(x)=\begin{cases}1&(x\in\Q)\\0&(x\in\R\setminus\Q)\end{cases}\end{align*}
$\Q$は有理数の集合,$\R$は実数の集合です.そのため,$\R\setminus\Q$は無理数の集合となります.
つまり,ディリクレ関数$f$は
- $f(4)=f\bra{\frac{1}{2}}=f\bra{\frac{4}{3}}=1$
- $f(-\sqrt{2})=f(\pi)=f(\log_{2}{5})=0$
のように,有理数を代入すると1を返し,無理数を代入すると0を返すような関数です.
ディリクレ関数がリーマン積分不可能であることを示すためには,これは有理数と無理数の稠密性を用います.
[有理数と無理数の稠密性]任意の実数$a$, $b$ ($a<b$)に対して,$a<c<b$となる有理数$c$,無理数$c$が存在する.
大雑把に言えば「数直線をどこまで拡大しても有理数と無理数が存在する」「有理数と無理数は極めて細かく入り組んでいる」ということですね.このため,上のディリクレ関数$y=f(x)$のグラフは「0と1を極めて細かく飛び移るグラフ」になっています.
リーマン積分は領域を縦にスライスしていくわけですが,[有理数と無理数の稠密性]よりどのスライスの中にも
- 高さ1の点
- 高さ0の点
が含まれますね.よって,長方形近似を作るとき,
- 全ての長方形の高さを1にする
- 全ての長方形の高さを0にする
のどちらも可能です.
しかし,「(スライスの最大幅)→0の極限により,いつでも長方形近似の面積和が「同じ値」に収束するとき,リーマン積分可能という」のでしたから,違う値に収束させられるディリクレ関数はリーマン積分不可能になるわけですね.
このように,「リーマン積分は不連続関数にあまり強くない」と言えるわけですね.
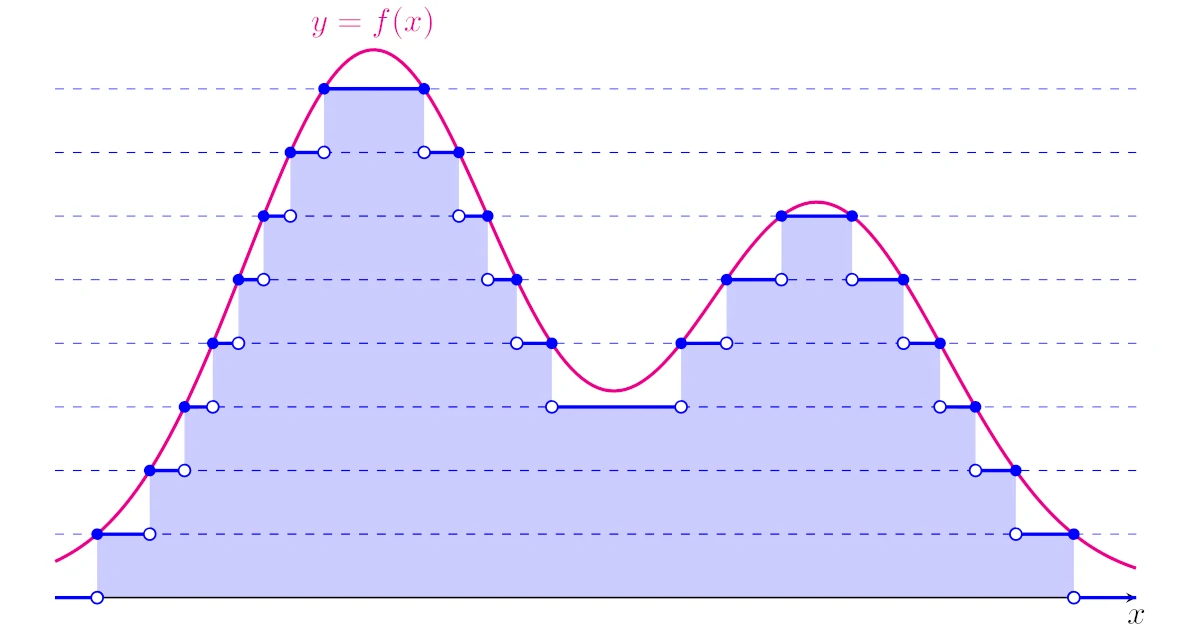
ルベーグ積分は値域に注目する積分
1900年頃,リーマン積分よりも不連続関数に強い積分として,アンリ・ルベーグ(Henri Lebesgue)は積分の新しい定義を考えました.現在ではこの積分をルベーグ積分とよびます.
リーマン積分が「縦切り」なら,ルベーグ積分は「横切り」ということができるのですが,これについて少し考えてみましょう.
ルベーグ積分は値域に注目して考える積分
簡単な問題を考えましょう.
次の$y=f(x)$のグラフをもつ関数$f$の水色領域の面積$\dint_{0}^{3}f(x)\,dx$を求めよ.
積分の計算を用いるまでもありませんね.
面積$\dint_{0}^{3}f(x)\,dx$は
- $2\times$($f(x)=2$となる$x$の集合の長さ)
- $3\times$($f(x)=3$となる$x$の集合の長さ)
- $1\times$($f(x)=1$となる$x$の集合の長さ)
の和に等しいから,
\begin{align*}\int_{0}^{3}f(x)\,dx=2\times\frac{3}{2}+3\times\frac{1}{2}+1\times1=\frac{11}{2}\end{align*}
である.
この解答のように,一般に有限個の値$\{\alpha_{1},\alpha_{2},\dots,\alpha_{n}\}$しか取らない関数$f$に対して,積分は
- $\alpha_{1}\times$($f(x)=\alpha_{1}$となる$x$の集合の長さ)
- $\alpha_{2}\times$($f(x)=\alpha_{2}$となる$x$の集合の長さ)
- ……
- $\alpha_{n}\times$($f(x)=\alpha_{n}$となる$x$の集合の長さ)
の和で求めることができます.
定義域に注目して近似和を考えるリーマン積分に対して,いま考えたように値域に注目して近似和を考える積分をルベーグ積分といいます.
ルベーグ積分ならディリクレ関数も積分できる
この考え方のもとで先ほどのディリクレ関数
\begin{align*}f(x)=\begin{cases}1&(x\in\Q)\\0&(x\in\R\setminus\Q)\end{cases}\end{align*}
を$0\le x\le 1$でルベーグ積分してみましょう.
ディリクレ関数のとりうる値は0と1でしたから,
- $0\times(\text{$f(x)=0$かつ$0\le x\le 1$となる$x$の集合の長さ})$
- $1\times(\text{$f(x)=1$かつ$0\le x\le 1$となる$x$の集合の長さ})$
の和がルベーグ積分ということになります.
このうち,前者は0をかけているのでもちろん0で,後者は1をかけており$f(x)=1$となる$x$は有理数なので
\begin{align*}\int_{0}^{1}f(x)\,dx=(\text{$0\le x\le 1$なる有理数$x$全部の集合の長さ})\end{align*}
となりますね.
しかし,有理数は数直線上で「まばら」な集合なので,「$0\le x\le 1$なる有理数$x$全部の集合の長さ」といわれてもあまりピンとこないかもしれません.
本来は「有理数の集合の長さ」というのものをきちんと定義すべきなのですが,ここでは結果だけを使うと実は「$0\le x\le 1$での有理数の集合の長さ」は0となります.
したがって,ディリクレ関数の積分は
\begin{align*}\int_{0}^{1}f(x)\,dx=0\end{align*}
と計算できるわけですね.
リーマン積分は横長の長方形で面積を考える
いま考えたルベーグ積分はとりうる値が有限個だったので有限和でしたが,一般には関数のとりうる値は有限個とは限りません.
そのような場合には横にスライスして近似和を考え,このスライスの幅を小さくしていくことでルベーグ積分を定義します.
繰り返しますが,リーマン積分では関数の定義域に注目して考えた一方で,関数の値域に注目して考えるのがルベーグ積分です.
この意味で先ほどは「リーマン積分が『縦切り』なら,ルベーグ積分は『横切り』」と説明していたわけですね.
ルベーグ積分の良さ
最後にルベーグ積分の良さをいくつか挙げます.
数学的に扱いやすい
微分と積分を扱う分野は「解析学」と呼ばれるのですが,例えば
- リーマン積分ができる関数列の極限関数でリーマン積分を考えられるとは限らない
- リーマン積分と極限の順序交換ができるための条件が面倒
など解析学としては,実は少々扱いづらいという欠点があります.
一方,ルベーグ積分ではこれらの欠点が大きく改善され
- ルベーグ積分ができる関数列の極限関数もルベーグ積分を考えられる
- ルベーグ積分と極限の順序交換ができるための条件が比較的簡単
となります.
また,少し専門的にはなりますが,ルベーグ積分は「完備性」と相性が良く関数解析学の理論を使うために好都合というのが,ルベーグ積分が重用される特に大きな理由です.
このように,ルベーグ積分は数学的に非常に扱いやすく,現代の解析学で用いる数学の多くはルベーグ積分です.たとえば,私の研究の専門分野である「非線形偏微分方程式論」では,ルベーグ積分がないと何もできないと言っても言い過ぎではありません.
確率論の準備になる
ルベーグ積分という理論の良さというわけではないのですが,学習者目線からの良さを挙げておきます.
ルベーグ積分はより広く測度論という分野に属します.測度論とは「長さや頻度などの量を測る理論」のことで,測度論に属する他のトピックとしては確率論が挙げられます.高校数学で確率といえば,場合の数の延長で扱われ微分積分とは関係なさそうに思えるかもしれませんが,実は専門的な確率論は微分積分を使い倒します.
さて,ルベーグ積分の考え方が理解できていると測度論の考え方にも馴染みやすくなります.
最近ではブラック・ショールズ方程式といった確率微分方程式の認知度が上がり始めており,この分野に入門するために確率論を学ぶ必要があり,そのために「まずはルベーグ積分を学ぼう」という方も少なからずいらっしゃいます.
このように,ルベーグ積分は測度論への入門としては,非常に良いトピックということができます.



コメント