一様可積分性をもつ確率変数列は,積分と極限の順序交換に関するヴィタリ(Vitali)の収束定理が成り立つのでした.
ヴィタリの収束定理は確率変数列の
- 一様可積分性
- 0への概収束
が分かっていれば適用でき,ルベーグの収束定理とは違って優関数をとってこなくても良い点で有用です.
この記事では
- 一様可積分性が成り立つための十分条件
- 一様可積分性が成り立つための必要十分条件
を順に説明します.
一連の記事はこちら
【確率変数の4つの収束|概収束,平均収束,確率収束,法則収束】
【一様可積分とヴィタリの収束定理|ルベーグの収束定理の一般化】
【確率変数列の一様可積分性の判定条件|十分条件と必要十分条件】←この記事
一様可積分性の復習
まずは一様可積分性の定義を確認しておきましょう.
[一様可積分]確率空間$(\Omega,\mathcal{F},\mathbb{P})$において,実数値確率変数列$\{X_n\}_{n\in\N}$が
\begin{align*}&\lim_{\lambda\to\infty}\sup_{n\in\N}\int_{\{|X_n|\ge\lambda\}}|X_n(\omega)|\,\mathbb{P}(d\omega)=0
\\&\bra{\iff\lim_{\lambda\to\infty}\sup_{n\in\N}\mathbb{E}\brc{|X_n|\mathbb{I}_{\{|X_n|\ge\lambda\}}}=0}\end{align*}
を満たすとき,$\{X_n\}_{n\in\N}$は一様可積分(uniformly integrable)であるという.
ただし,$\mathbb{E}$は期待値,集合$A\subset\Omega$に対して$\mathbb{I}_{A}$は$A$上の定義関数です:
\begin{align*}\mathbb{E}[X]=\int_{\Omega}X(\omega)\,\mathbb{P}(d\omega),\quad
\mathbb{I}_{A}(\omega)=\begin{cases}1,&\omega\in A,\\0,&\omega\notin A.\end{cases}\end{align*}
要するに$\{X_n\}$が一様可積分であるとは,「$|X_n|$が$\lambda$以上となるところでの$X_n$の期待値」が$n$によらず一様に$\lambda\to\infty$で0に近付くということですね.
一様可積分性の十分条件
一様可積分の十分条件を2つ示します.
十分条件1(優関数の存在)
確率関数列に優関数が存在すれば,一様可積分となります.
確率変数列$\{X_n\}_{n\in\N}$について,可積分な確率変数$X$が存在して,任意の$n\in\N$, $\omega\in\Omega$に対して$|X_n(\omega)|\le X(\omega)$が成り立てば,$\{X_n\}_{n\in\N}$は一様可積分である.
確率変数族$\{|X|\mathbb{I}_{\{|X|\ge\lambda\}}\}_{\lambda>0}$について,
- $\{|X|\mathbb{I}_{\{|X|\ge\lambda\}}\}_{\lambda>0}$は$\lambda\to0$で0に概収束し,
- 任意の$\omega\in\Omega$に対して$\abs{|X(\omega)|\mathbb{I}_{\{|X|\ge\lambda\}}(\omega)}\le X(\omega)$が成り立ち,
- 仮定より$X$は可積分である.
よって,ルベーグの収束定理が適用できて,
\begin{align*}\lim_{\lambda\to\infty}\mathbb{E}\brc{|X|\mathbb{I}_{\{|X|\ge\lambda\}}}=0\end{align*}
が成り立つ.仮定より,任意の$n\in\N$に対して$|X_n|\le X$だから,
\begin{align*}\mathbb{E}\brc{|X_n|\mathbb{I}_{\{|X_n|\ge\lambda\}}}
\le&\mathbb{E}\brc{|X|\mathbb{I}_{\{|X_n|\ge\lambda\}}}
\\\le&\mathbb{E}\brc{|X|\mathbb{I}_{\{|X|\ge\lambda\}}}
\\\to&0\quad(\lambda\to\infty)\end{align*}
が成り立つ.よって,$\{X_n\}_{n\in\N}$は一様可積分である.
例えば,可積分な実数値確率変数$X$に対して,$X=X_1=X_2=\dots$で定まる確率変数列$\{X_n\}_{n\in\N}$(全ての項が$X$の確率変数列)は一様可積分です.
実際,$X$が可積分であることから,$|X|$も可積分で$|X_n|\le |X|$を満たします.
すなわち,$|X|$を優関数にとれるので,$\{X\}_{n\in\N}$は一様可積分となります.
十分条件2(1より大きい冪でも期待値が有限)
1次より大きい増大をもち,期待値を有限にする正値関数が存在すれば,一様可積分となります.
確率変数列$\{X_n\}_{n\in\N}$について,ボレル可測関数$\psi:\R\to\R_{>0}$が存在して,
\begin{align*}\lim_{|x|\to\infty}\dfrac{|x|}{\psi(x)}=0,\quad
\sup_{n\in\N}\mathbb{E}[\psi(X_n)]<\infty\end{align*}
が同時に成り立てば,$\{X_n\}_{n\in\N}$は一様可積分である.
$M:=\sup\limits_{n\in\N}\mathbb{E}[\psi(X_n)]$とおき,任意の$\epsilon>0$をとる.$\lim\limits_{|x|\to\infty}\dfrac{|x|}{\psi(x)}=0$より,ある$R>0$が存在して,
\begin{align*}|x|>R\Ra\dfrac{|x|}{\psi(x)}<\frac{\epsilon}{M}\end{align*}
が成り立つ.よって,
\begin{align*}\mathbb{E}\brc{|X_n|\mathbb{I}_{\{|X_n|\ge R\}}}
&=\mathbb{E}\brc{\frac{|X_n|}{\psi(X_n)}\cdot\psi(X_n)\mathbb{I}_{\{|X_n|\ge R\}}}
\\&\le\mathbb{E}\brc{\frac{\epsilon}{M}\psi(X_n)\mathbb{I}_{\{|X_n|\ge R\}}}
\\&=\frac{\epsilon}{M}\mathbb{E}\brc{\psi(X_n)\mathbb{I}_{\{|X_n|\ge R\}}}
\\&\le\frac{\epsilon}{M}\mathbb{E}[\psi(X_n)]
\le\frac{\epsilon}{M}\cdot M
=\epsilon\end{align*}
が$n\in\N$によらず成り立つ.よって,$\{X_n\}_{n\in\N}$は一様可積分である.
この系として,期待値の列$\{\mathbb{E}[|X_n|^p]\}$($p>1$)が一様に有界な確率変数列$\{X_n\}$は一様可積分であることが分かります.
確率変数列$\{X_n\}$を考える.ある$p>1$が存在して,$\sup\limits_{n\in\N}\mathbb{E}[|X_n|^p]<\infty$なら$\{X_n\}$は一様可積分である.
関数列$\{X_n\}_{n\in\N}$が$p$乗可積分であるとする:$\sup\limits_{n\in\N}\mathbb{E}[|X_n|^p]<\infty$.このとき,$\psi(x)=|x|^p$ととれば,
\begin{align*}\lim_{|x|\to\infty}\frac{|x|}{\psi(x)}
=&\lim_{|x|\to\infty}\frac{|x|}{|x|^p}
\\=&\lim_{|x|\to\infty}|x|^{1-p}
=0,
\\\sup_{n\in\N}\mathbb{E}[\psi(X_n)]
=&\sup_{n\in\N}\mathbb{E}[|X_n|^p]
<\infty\end{align*}
が成り立つから,$\{X_n\}_{n\in\N}$は一様可積分である.
一様可積分性の必要十分条件
次に,一様可積分の必要十分条件について説明します.
この必要十分条件を用いれば,一様可積分な2つの確率変数列の和も一様可積分であることを容易に示すことができます.
一様可積分性の必要十分条件
以下は一様可積分の必要十分条件です.
実数値確率変数列$\{X_n\}_{n\in\N}$について,$\{X_n\}_{n\in\N}$が一様可積分であることと,次が同時に成り立つことは同値である.
- $\sup\limits_{n\in\N}\mathbb{E}[|X_n|]<\infty$が成り立つ.
- 任意の$\epsilon>0$に対して,ある$\delta>0$が存在して,$A\in\mathcal{F}$が$\mathbb{P}(A)<\delta$を満たすなら$\sup\limits_{n\in\N}\mathbb{E}[|X_n|\mathbb{I}_{A}]<\epsilon$が成り立つ.
[(1)⇒(2)の証明]実数値確率変数列$\{X_n\}_{n\in\N}$が一様可積分であるとする.
このとき,1つ目の条件$\sup\limits_{n\in\N}\mathbb{E}[|X_n|]<\infty$が成り立つことは前回の記事で示したから,2つ目の条件を示す.
任意に$\epsilon>0$をとる.$\{X_n\}_{n\in\N}$が一様可積分であることから,ある$R>0$が存在して,
\begin{align*}\sup_{n\in\N}\mathbb{E}\brc{|X_n|\mathbb{I}_{\{|X_n|\ge R\}}}<\frac{\epsilon}{2}\end{align*}
が成り立つ.ここで,$A\in\mathcal{F}$が$\mathbb{P}(A)<\frac{\epsilon}{2R}$とすると,
\begin{align*}&\sup_{n\in\N}\mathbb{E}[|X_n|\mathbb{I}_{A}]
\\=&\sup_{n\in\N}\bra{\mathbb{E}\brc{|X_n|\mathbb{I}_{A\cap\{|X_n|\ge R\}}}+\mathbb{E}\brc{|X_n|\mathbb{I}_{A\cap\{|X_n|<R\}}}}
\\\le&\sup_{n\in\N}\bra{\mathbb{E}\brc{|X_n|\mathbb{I}_{\{|X_n|\ge R\}}}+\mathbb{E}\brc{R \mathbb{I}_{A\cap\{|X_n|<R\}}}}
\\\le&\sup_{n\in\N}\bra{\mathbb{E}\brc{|X_n|\mathbb{I}_{\{|X_n|\ge R\}}}+R\mathbb{E}\brc{\mathbb{I}_{A}}}
\\\le&\bra{\sup_{n\in\N}\mathbb{E}\brc{|X_n|\mathbb{I}_{\{|X_n|<R\}}}}+R\mathbb{P}(A)
\\<&\frac{\epsilon}{2}+R\cdot\frac{\epsilon}{2R}=\epsilon\end{align*}
となって,2つ目の条件も成り立つ.
[十分性の証明]実数値確率変数列$\{X_n\}_{n\in\N}$が2つの条件を同時に満たすとし,1つ目の条件について$M:=\sup\limits_{n\in\N}\mathbb{E}[|X_n|]<\infty$とする.
任意の$\lambda>0$に対して,$\delta=\frac{2M}{\lambda}$とすると,
\begin{align*}&\mathbb{P}\bra{\set{\omega\in\Omega}{|X_n(\omega)|\ge\lambda}}
=\mathbb{E}\brc{\mathbb{I}_{\{|X_n|\ge\lambda\}}}
\\&\le\mathbb{E}\brc{\frac{|X_n|}{\lambda}\mathbb{I}_{\{|X_n|\ge\lambda\}}}
=\frac{1}{\lambda}\mathbb{E}\brc{|X_n|\mathbb{I}_{\{|X_n|\ge\lambda\}}}
\\&\le\frac{1}{\lambda}\mathbb{E}\brc{|X_n|}
\le\frac{M}{\lambda}=\frac{\delta}{2}<\delta\end{align*}
が成り立つから,2つ目の条件より
\begin{align*}\sup_{n\in\N}\mathbb{E}[|X_n|\mathbb{I}_{\{|X_n|\ge\lambda\}}]<\epsilon\end{align*}
が成り立つ.すなわち,$\{X_n\}_{n\in\N}$は一様可積分である.
応用(一様可積分性と和)
いまみた必要十分条件を用いると,次のように一様可積分な確率変数列の和は一様可積分となることが証明できます.
一様可積分な2つの確率変数列$\{X_n\}_{n\in\N}$, $\{Y_n\}_{n\in\N}$に対して,$\{X_n+Y_n\}_{n\in\N}$は一様可積分である.
一様可積分性の必要十分条件より,$\sup\limits_{n\in\N}\mathbb{E}[|X_n|]<\infty$, $\sup\limits_{n\in\N}\mathbb{E}[|Y_n|]<\infty$が成り立つから,
\begin{align*}%\sup_{n\in\N}\mathbb{E}[|X_n+Y_n|]
\le\sup_{n\in\N}\mathbb{E}[|X_n|+|Y_n|]
\\&=\sup_{n\in\N}\bra{\mathbb{E}[|X_n|]+\mathbb{E}[|Y_n|]}
\\&\le\bra{\sup_{n\in\N}\mathbb{E}[|X_n|]}+\bra{\sup_{n\in\N}\mathbb{E}[|Y_n|]}
\\&<\infty\end{align*}
が成り立つ.
また,一様可積分性の必要十分条件より,任意の$\epsilon>0$に対して,ある$\delta,\eta>0$が存在して,$A,B\in\mathcal{F}$が$\mathbb{P}(A)<\delta$, $\mathbb{P}(B)<\eta$を満たすなら$\sup\limits_{n\in\N}\mathbb{E}[|X_n|\mathbb{I}_{A}]<\frac{\epsilon}{2}$, $\sup\limits_{n\in\N}\mathbb{E}[|Y_n|\mathbb{I}_{B}]<\frac{\epsilon}{2}$が成り立つ.
よって,$\mathbb{P}(C)<\min\{\delta,\eta\}$を満たす$C\in\mathcal{F}$をとると,
\begin{align*}\sup_{n\in\N}\mathbb{E}[|X_n|\mathbb{I}_{C}]<\frac{\epsilon}{2},\quad
\sup_{n\in\N}\mathbb{E}[|Y_n|\mathbb{I}_{C}]<\frac{\epsilon}{2}\end{align*}
が成り立つ.よって,
\begin{align*}&\sup_{n\in\N}\mathbb{E}[|X_n+Y_n|\mathbb{I}_{C}]
\le\sup_{n\in\N}\mathbb{E}[(|X_n|+|Y_n|)\mathbb{I}_{C}]
\\&\le\sup_{n\in\N}\bra{\mathbb{E}[|X_n|\mathbb{I}_{C}]+\mathbb{E}[|Y_n|\mathbb{I}_{C}]}
\\&\le\bra{\sup_{n\in\N}\mathbb{E}[|X_n|\mathbb{I}_{C}]}+\bra{\sup_{n\in\N}\mathbb{E}[|Y_n|\mathbb{I}_{C}]}
\\&<\frac{\epsilon}{2}+\frac{\epsilon}{2}<\epsilon\end{align*}
が成り立つ.
以上より,$\{X_n+Y_n\}_{n\in\N}$は一様可積分性の必要十分条件を満たすことが分かったから,$\{X_n+Y_n\}_{n\in\N}$は一様可積分である.
参考文献
確率論
[舟木直久 著/朝倉書店]
本書は確率論の入門書で,全体を通して丁寧に書かれています.
第1章では確率論の概説がなされており,例えば「大数の弱法則」「大数の強法則」にまで平易な説明で触れられているのが嬉しいです.
ただし,本書の「まえがき」に書かれているように,第2章から第5章は大学3年〜4年相当の確率論の内容となっているので,第2章以降を読むにはそれなりの基礎が必要となります.
第6章,第7章では代表的な確率過程である「マルチンゲール」「マルコフ過程」が解説されています.
本書は全体を通して「なぜその概念を学ぶ必要があるのか」という動機付けが大切にされており,新しい概念を前向きに理解しやすい点が優れている好著となっています.

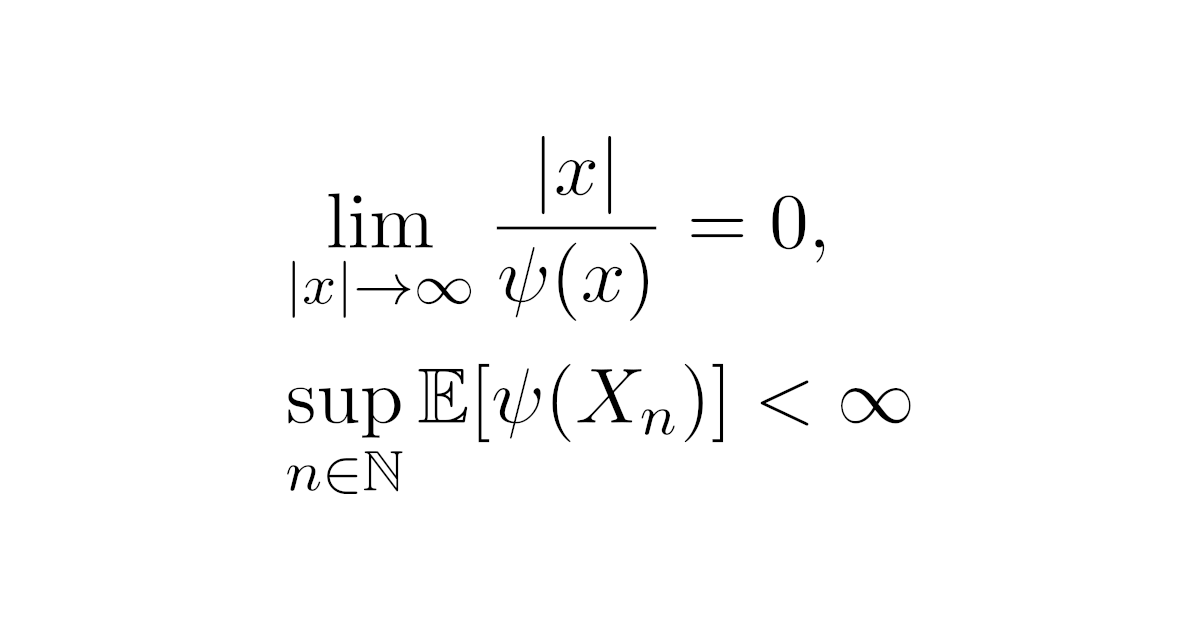

コメント