自由シュレディンガー(Schrödinger)方程式とは,線形の偏微分方程式
\begin{align*}i\partial_{t}u(t,x)+\Delta u(t,x)=0\end{align*}
のことで,非線形シュレディンガー方程式を考える際にも基本となる方程式です.
自由というのは「非線形項がなく自由に振る舞う」という意味で,散乱理論でよく用いられる呼び方です.
ここに
\begin{align*}i=\sqrt{-1},\quad
\partial_{t}=\frac{\partial}{\partial t},\quad
\Delta=\sum_{i=1}^N\frac{\partial^2}{\partial x_i^2}\end{align*}
です.つまり,$i$は虚数単位,$\partial_{t}$は$t$に関する偏微分,$\Delta$はラプラシアンです.
自由シュレディンガー方程式の初期値問題の解$u$は,ストーンの定理を用いて$u(t,x)=e^{it\Delta}u_0(x)$と表すことができ,この$e^{it\Delta}$を自由シュレディンガー発展作用素といいます.
ストーンの定理を用いるためには自由シュレディンガー発展作用素$e^{it\Delta}$が強連続ユニタリ群であることを述べる必要があり,そのためにこの記事では自由シュレディンガー方程式の解を考えます.
一連の記事はこちら
【自由シュレディンガー方程式の基本解とユニタリ群】←今の記事
【シュレディンガー方程式の基本解の[$L^pL^q$評価]の導出】
【シュレディンガー方程式のストリッカーツ評価の導出】
自由シュレディンガー方程式の基本解
まずは自由シュレディンガー方程式の基本解の定義を述べ,直接計算して解の形を求めましょう.
基本解の定義
他の方程式にも適用できるより広い基本解の定義はありますが,シュレディンガー方程式に限れば基本解は以下のように定義されます.
[基本解]自由シュレディンガー方程式の初期値問題
\begin{align*}\begin{cases}
i\partial_{t}u(t,x)+\Delta u(t,x)=0, & (t,x)\in\R\times\R^d,\\
u(0,x)=u_0(x), & x\in\R^d\\
\end{cases}\end{align*}
の$u,u_0\in\mathcal{S}(\R^d)$の解$u$をシュレディンガー方程式の基本解(fundamental solution)または自由解(free solution)という.
なお,$\mathcal{S}(\R^d)$はシュワルツ空間(急減少関数の空間)です.
基本解は厳密には$\mathcal{S}'(\R^d)$における超関数解として定めます.
そのため,以下の計算では単純な関数としてみると怪しいところが散見されますが,超関数として考えると全て正当化されます.
基本解の形
それではシュレディンガー方程式の基本解の形を求めましょう.
上の$d$次元の自由シュレディンガー方程式について,$u,u_0\in\mathcal{S}(\R^d)$なら基本解$u$は
\begin{align*}u(x)
&=\mathcal{F}^{-1}\brc{e^{-it|\xi|^2}\widehat{u_0}(\xi)}(x)
\\&=\frac{1}{(4\pi it)^{d/2}}\int_{\R^d}e^{-\frac{|x-y|^2}{4it}}u_0(y)\,dy\end{align*}
となる.ただし,$\mathcal{F}$はフーリエ変換である:
\begin{align*}&\hat{f}(\xi)=\mathcal{F}[f](\xi):=\frac{1}{(2\pi)^{d/2}}\int_{\R^d}e^{-ix\cdot\xi}f(x)\,dx,
\\&\check{f}(x)=\mathcal{F}^{-1}[f](x):=\frac{1}{(2\pi)^{d/2}}\int_{\R^d}e^{i\xi\cdot x}f(\xi)\,d\xi\end{align*}
$i\partial_{t}u(t,x)+\Delta u(t,x)=0$の両辺に$x$についてフーリエ変換を施すと,
\begin{align*}i\partial_{t}\hat{u}(t,\xi)-|\xi|^2\hat{u}(t,\xi)=0\end{align*}
となる.両辺に$-ie^{it|\xi|^2}$をかけて
\begin{align*}\pd{}{t}\bra{e^{it|\xi|^2}\hat{u}(t,\xi)}=0\end{align*}
となり,$t$について両辺積分すると
\begin{align*}&\int_{0}^{t}\pd{}{\tau}\bra{e^{i\tau|\xi|^2}\hat{u}(\tau,\xi)}\,d\tau=0
\\&\iff e^{it|\xi|^2}\hat{u}(t,\xi)-e^{i0|\xi|^2}\hat{u}(0,\xi)=0
\\&\iff\hat{u}(t,\xi)=e^{-it|\xi|^2}\widehat{u_0}(\xi)
\\&\iff u(t,x)=\mathcal{F}^{-1}\brc{e^{-it|\xi|^2}\widehat{u_0}}(x)
\\&\iff u(t,x)=\frac{1}{(2\pi)^{d/2}}\bra{\mathcal{F}^{-1}\brc{e^{-it|\xi|^2}}*u_0}(x)\end{align*}
となる.ここに,$f*g$は$f$と$g$の合成積である.計算により
\begin{align*}\frac{1}{(2\pi)^{d/2}}\mathcal{F}^{-1}\brc{e^{-it|\xi|^2}}(x)
=\frac{1}{(4\pi it)^{d/2}}e^{-\frac{|x|^2}{4it}}
=:S_t(x)\end{align*}
となるから,解$u$は
\begin{align*}u(x)&=(S_t*u_0)(x)
\\&=\int_{\R^d}S_t(x-y)u_0(y)\,dy
\\&=\frac{1}{(4\pi it)^{d/2}}\int_{\R^d}e^{-\frac{|x-y|^2}{4it}}u_0(y)\,dy\end{align*}
となる.
この証明で定義した$S_t$を自由シュレディンガー核といいます.
自由シュレディンガー発展作用素
初期値$u_0\in\mathcal{S}(\R^d)$からシュレディンガー方程式の基本解を与える作用素を自由シュレディンガー発展作用素といい,この記事では自由シュレディンガー発展作用素を$T_t$で表します:
\begin{align*}T_{t}u_0:=S_t*u_0.\end{align*}
一般にノルム空間$\mathcal{X}$とBanach空間$\mathcal{Y}$に対して,$\mathcal{X}$上で稠密な定義域をもつ有界線形作用素$\mathcal{X}\to\mathcal{Y}$は$X$上の有界線形作用素に一意的に拡張できるのでした.
このことを用いると以下を証明できます.
任意の$t\in T$に対して,自由シュレディンガー発展作用素$T_t:\mathcal{S}(\R^d)\to\mathcal{S}(\R^d)$は定義域を$L^2(\R^d)$とする$L^2(\R^d)$上の有界線形作用素に一意に拡張できる.
$L^2(\R^d)$ノルムを$\|\cdot\|_2$で表す.
[1]合成積の線形性から,任意の$f,g\in L^2(\R^d)$, $\alpha,\beta\in\C$に対して
\begin{align*}{T_t}(\alpha f+\beta g)=&{S_t}*(\alpha f+\beta g)
\\&=\alpha{S_t}*f+\beta{S_t}*g
\\&=\alpha{T_t}f+\beta{T_t}g\end{align*}
となるので,$T_t$は線形である.
[2]任意の$f\in L^2(\R^d)$に対して,プランシュレルの定理と$\abs{e^{-it|\xi|^2}}=1$を用いることにより
\begin{align*}\|{T_t}f\|_2&=\|{S_t}*f\|_2=\nor{\mathcal{F}^{-1}\brc{e^{-it|\xi|^2}\hat{f}}}_2
\\&=\nor{e^{-it|\xi|^2}\hat{f}}_2=\nor{\hat{f}}_2=\|f\|_2\end{align*}
となって,$T_t$は有界である.
[1],[2]と
- $T_t$はSchwartz空間$\mathcal{S}(\R^d)$で定義されていること
- $\mathcal{S}(\R^d)$の$\|\cdot\|_2$ノルムによる閉包が$L^2(\R^d)$であること
を併せると,関数解析の一般論から$T_t$は定義域を$L^2(\R^d)$とする$L^2(\R^d)$上の有界線形作用素に一意に拡張できる.
この証明から分かるように,$T_t$は$L^2$有界よりも強く$L^2$等長となっていますね.
強連続ユニタリ群
ここでは強連続ユニタリ群を定義して,自由シュレディンガー発展作用素の族$\{T_t\}_{t\in\R}$が強連続ユニタリ群であることを示しましょう.
強連続ユニタリ群
一般にHilbert空間上の有界線形作用素の族がユニタリ群であるとは,次のように定義されます.
[強連続ユニタリ群]Hilbert空間$\mathcal{H}$上の有界線形作用素の族$\{T_t\}_{t\in\R}$が$\mathcal{H}$上ユニタリ群であると
- 任意の$s,t\in\R$に対して,${T_s}{T_t}=T_{s+t}$である.
- $T_0=I$である.ただし,$I$は$\mathcal{H}$上の恒等作用素である.
- 任意の$f\in\mathcal{H}$, $t_0\in\R$に対して,$\lim\limits_{h\to 0}\|T_{t_0+h}f-T_{t_0}f\|_{\mathcal{H}}=0$である.
- 任意の$t\in\R$に対して,$T_{t}$はユニタリ作用素(全単射かつ等長)である.
を満たすことをいう.
条件1〜3のみを満たす$\{T_t\}_{t\in\R}$を強連続群や$C_0$群などといいます.
自由シュレディンガー発展作用素
自由シュレディンガー発展作用素の族$\{T_t\}_{t\in\R}$は$L^2(\R^N)$上強連続ユニタリ群である.
任意に$s,t\in\R$, $f\in L^2(\R^N)$をとる.
\begin{align*}{T_s}{T_t}f&=\mathcal{F}_{\xi}^{-1}\brc{e^{is|\xi|^2}\mathcal{F}_{x}\brc{\mathcal{F}_{\xi}^{-1}\brc{e^{it|\xi|^2}\hat{f}}}}
\\&=\mathcal{F}_{\xi}^{-1}\brc{e^{is|\xi|^2}\bra{e^{it|\xi|^2}\hat{f}}}
\\&=\mathcal{F}_{\xi}^{-1}\brc{e^{i(s+t)|\xi|^2}\hat{f}}
=T_{s+t}f\end{align*}
だから,${T_s}{T_t}=T_{s+t}$が成り立つ.
フーリエ変換が$L^2(\R^N)$のユニタリ作用素であることに注意すると,
\begin{align*}{T_0}f=\mathcal{F}^{-1}\brc{e^{i0|\xi|^2}\hat{f}}=\mathcal{F}^{-1}\brc{\hat{f}}=f\end{align*}
となって,$T_0=I$が成り立つ.
フーリエ変換の線形性,$L^2$等長性と,ノルムの連続性から
\begin{align*}&\lim_{h\to0}\|T_{t+h}f-{T_t}f\|_2
\\&=\lim_{h\to0}\nor{\mathcal{F}^{-1}\brc{e^{i(t+h)|\xi|^2}\hat{f}}-\mathcal{F}^{-1}\brc{e^{it|\xi|^2}\hat{f}}}_2
\\&=\lim_{h\to0}\nor{\mathcal{F}^{-1}\brc{\bra{e^{i(t+h)|\xi|^2}-e^{it|\xi|^2}}\hat{f}}}_2
\\&=\lim_{h\to0}\nor{e^{it|\xi|^2}\bra{e^{ih|\xi|^2}-1}\hat{f}}_2
\\&=\nor{\lim_{h\to0}e^{it|\xi|^2}\bra{e^{ih|\xi|^2}-1}\hat{f}}_2=\|0\|_{2}=0\end{align*}
となる.
先ほど示したように$T_t$は$L^2(\R^N)$全体で定義される等長作用素である.また,任意の$g\in L^2(\R^d)$に対して
\begin{align*}g=T_0g=T_{t}(T_{-t}g)\end{align*}
であり$T_{-t}g$だから$T_t$は全射で,$f\in L^2(\R^d)$が${T_t}f=0$を満たせば,左から$T_{-t}$を作用させて$f=0$となるから$T_t$は単射である.
ストーンの定理の適用
次の定理をストーンの定理といいます.
[ストーンの定理]$\{T_t\}_{t\in\R}$をHilbert空間$\mathcal{H}$全体で定義された$\mathcal{H}$上の有界線形作用素の族とする.このとき,$\{T_t\}_{t\in\R}$がユニタリ群であるためには,$\mathcal{H}$上の自己共役作用素$A$が存在して,$T_t=e^{itA}$を満たすことが必要十分である.
ストーンの定理より,自由シュレディンガー発展作用素の族$\{T_t\}$のユニタリ群であることから,$L^2(\R^d)$上の自己共役作用素$A$が存在して$T_t=e^{itA}$と表されます.
このとき,任意の$f\in L^2(\R^d)$に対して
\begin{align*}Af=-i\partial_{t}(e^{itA}f)|_{t=0}=-i\partial_{t}(T_tf)|_{t=0}\end{align*}
となります.$T_tf$は自由シュレディンガー方程式の解なので,
\begin{align*}i\partial_{t}(T_tf)+\Delta (T_tf)=0&\iff -i\partial_{t}(T_tf)=\Delta (T_tf)
\\&\Ra -i\partial_{t}(T_tf)|_{t=0}=\Delta (T_0f)
\\&\iff -i\partial_{t}(T_tf)|_{t=0}=\Delta f\end{align*}
なので,$Af=\Delta f$が得られ,$A=\Delta$となりますね.
このことから,ラプラシアン$\Delta$は$L^2(\R^d)$の自己共役作用素であり,自由シュレディンガー発展作用素は$e^{it\Delta}$とスッキリ表せることが分かりました.
以上をまとめると,以下のようになります.
自由シュレディンガー方程式の初期値問題
\begin{align*}\begin{cases}i\partial_{t}u(t,x)+\Delta u(t,x)=0, & (t,x)\in\R\times\R^d,\\
u(0,x)=u_0(x), & x\in\R^d\\\end{cases}\end{align*}
の$u,u_0\in\mathcal{S}(\R^d)$の解は
\begin{align*}e^{it\Delta}u_0(x)
=&\mathcal{F}\brc{e^{-it|\xi|^2}\hat{u_0}(\xi)}(x)
\\=&\frac{1}{(4\pi it)^{N/2}}\int_{\R^d}e^{-\frac{|x-y|^2}{4it}}u_0(y)\,dy\end{align*}
と表せる.
次の記事では,シュレディンガー方程式の基本解の基礎的な評価である$L^pL^q$評価を解説します.

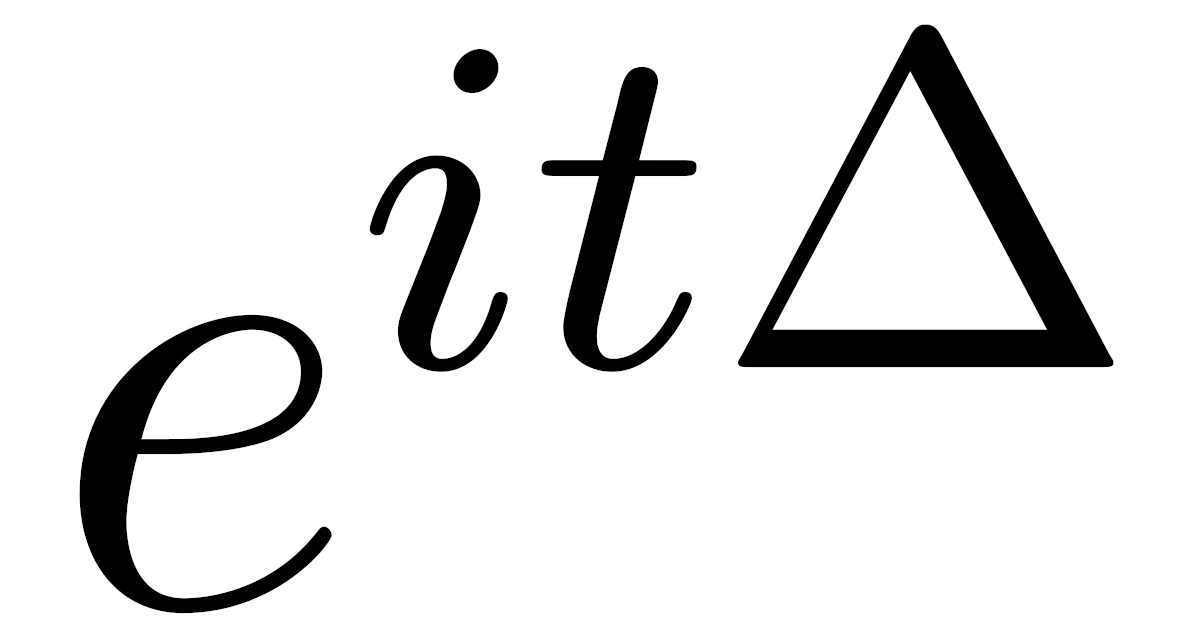
コメント