Hilbert空間上の有界線形作用素の族$\{T_t\}_{t\in\R}$が強連続ユニタリ群になるための必要十分条件を与える定理を述べたストーン(Stone)の定理は偏微分方程式論などにおいて基本的な定理として知られています.
類似の定理としてはHille-Yosidaの定理があり,こちらはBanach空間上の線形作用素$A$が半群$\{T_t\}_{t\in\R}$の生成作用素となる必要十分条件を述べる定理です.
Hille-Yosidaの定理を用いることでStoneの定理を証明することができますが,歴史的にはStoneの定理の方が先に証明されています.
また,Stoneの定理はHilbert空間の有界線形作用素の場合に限るためシンプルで分かりやすいので,Hille-Yosidaの定理の特別な場合としてStoneの定理を理解しておくことも大切です.
予備知識
Stoneの定理を述べる前に,必要な知識を簡単に準備します.
この記事では$\mathcal{H}$を複素Hilbert空間とします.
作用素の空間
まずは有界線形作用素の空間についてまとめます.
作用素$\mathcal{H}\to\mathcal{H}$を$\mathcal{H}$上の作用素という.また,定義域が$\mathcal{H}$であるような$\mathcal{H}$上の有界線形作用素$T$の作用素$T$全部の空間を$B(\mathcal{H})$と表す.
作用素$T:\mathcal{H}\to\mathcal{H}$といった場合でも,必ずしも$T$は$\mathcal{H}$全体で定義されているとは限らないことを思い出しておきましょう.
$T,S\in B(\mathcal{H})$, $\alpha\in\C$に対して,和$T+S$とスカラー倍$\alpha T$を
- $(T+S)f:=Tf+Sf$ $(f\in\mathcal{H})$
- $(\alpha T)f:=\alpha(Tf)$ $(f\in\mathcal{H})$
で定めると,$B(\mathcal{H})$は線形空間となります.
さらに,作用素ノルム
\begin{align*}\|T\|=\|T\|_{B(\mathcal{H})}
:=\sup\limits_{\|f\|_{\mathcal{H}}=1}\|Tf\|_{\mathcal{H}}\end{align*}
により$B(\mathcal{H})$はBanach空間となります.
なお,$T,S\in B(\mathcal{H})$の積$TS$を$(TS)f:=T(Sf)$ ($f\in\mathcal{H}$)で定めると,$TS$は$B(\mathcal{H})$に属しますね.
作用素の強連続性
次に,作用素の強連続性の定義を確認します.
作用素の族$\{T_t\}_{t\in\R}$が$t_0\in\R$で強連続であるとは,任意の$f\in\mathcal{H}$に対して,
\begin{align*}\lim_{h\to0}\|T(t_0+h)f-T(t_0)f\|_{\mathcal{H}}=0\end{align*}
を満たすことをいう.
なお,
- 作用素の空間の強連続
- それ以外の空間の強連続
は異なることに注意してください.
作用素の空間でない空間$\mathcal{X}$においては,$\|\cdot\|_{\mathcal{X}}$に関する普通の連続性を(弱連続と区別して)強連続というのでした.
一方,有界線形作用素の空間$B(\mathcal{H})$においては,上の定義のような性質を強連続性といい,作用素のノルム$\|\cdot\|_{B(\mathcal{H})}$に関する普通の連続性をノルム連続といいます.
したがって,
- $\mathcal{X}$における「強連続」
- $B(\mathcal{H})$における「ノルム連続」
は対応しますが,$\mathcal{X}$における「弱連続」と$B(\mathcal{H})$における「強連続」は対応関係にないことに注意してください.
強連続群,ユニタリ群と生成作用素
次に,強連続群(ユニタリ群)と生成作用素について確認します.
$t\in\R$をパラメータとする$B(\mathcal{H})$の族$\{T_t\}_{t\in\R}$が
- 任意の$t,s\in\R$に対して,$T_{t}T_{s}=T_{t+s}$
- $T_0=I$ ($I$は$\mathcal{H}$上の恒等作用素)
- $\{T_t\}_{t\in\R}$は$\R$上強連続.
を満たすとき,$\{T_t\}_{t\in\R}$を$\mathcal{H}$上の強連続群 ($C_0$群)という.加えて,
- 任意の$t\in\R$に対して,$T_{t}$は同型,すなわち全単射かつ等長である.
が成り立っているとき,$\{T_t\}_{t\R}$を$\mathcal{H}$上のユニタリ群という.
強連続「群」ということからも分かるように,
- 条件1から,$(T_{t}T_{s})T_{r}=T_{t+s}T_{r}=T_{(t+s)+r}=T_{t+(s+r)}=T_{t}T_{s+r}=T_{t}(T_{s}T_{r})$なので結合法則をみたし,
- 条件2から,$T_{0}T_{t}=T_{0+t}=T_{t}$, $T_{t}T_{0}=T_{t+0}=T_{t}$をみたし,
- 条件1と条件2から,$T_{t}T_{-t}=T_{t+(-t)}=T_{0}=I$, $T_{-t}T_{t}=T_{(-t)+t}=T_{0}=I$をみたすので,
$\{T_t\}_{t\in\R}$は$T_{0}$を単位元とし,$T_{t}$の逆元が$T_{-t}$であるような代数群となりますね.
このように,条件1,2からは代数的な性質が得られるわけですね.
この強連続群$\{T_t\}_{t\in\R}$の,いわば$t=0$での「導関数」に相当する作用素を生成作用素といいます.
$\mathcal{H}$上の強連続群$\{T_{t}\}_{t\in\R}$に対して,
\begin{align*}&D(A)=\set{f\in\mathcal{H}}{\exi g\in\mathcal{H}\ \mrm{s.t.}\ \lim_{h\to0}\frac{T_{h}f-f}{h}=g},
\\&Af=\lim_{h\to0}\frac{T_{h}f-f}{h}\quad(f\in D(A))\end{align*}
で定まる$\mathcal{H}$上の作用素$A$を$\{T_{t}\}_{t\in\R}$の生成作用素(無限小生成作用素)といい,このとき$T_{t}=e^{tA}$と表す.
生成作用素は指数を作用素に拡張したものと見ることもできますね.
自己共役作用素
一般に,ノルム空間$\mathcal{X}$, $\mathcal{Y}$に対して,線形作用素$T:\mathcal{X}\to\mathcal{Y}$の定義域$D(T)$が$\mathcal{X}$で稠密なら,$T$の共役作用素$T^*:\mathcal{Y}^*\to\mathcal{X}^*$が定義できます.
Rieszの定理からHilbert空間$\mathcal{H}$は自身の共役空間$\mathcal{H}^{*}$と同型($\mathcal{H}^{*}\cong\mathcal{H}$)でしたから,線形作用素$T$の定義域$D(T)$が$\mathcal{H}$上で稠密なら,$T$の共役作用素$T^*$も$\mathcal{H}$上の作用素となります.
これについて,以下のように定義します.
$\mathcal{H}$上の線形作用素$T$の定義域$D(T)$が$\mathcal{H}$上で稠密であり,$T\subset T^{*}$が成り立つとき$T$は対称作用素 (symmetric operator)であるという.さらに,$D(T)=D(T^{*})(=\mathcal{H})$であれば$T$は自己共役作用素 (self-adjoint operator)であるという.
最初の「定義域$D(T)$が$\mathcal{H}$上で稠密であり」の部分は$T$の共役作用素$T^*$が定義できるためにあるだけです.
また,一般に作用素$T$, $S$に対して
- $D(T)\subset D(S)$
- 任意の$f\in D(T)$に対して,$Tf=Sf$が成り立つ
の2条件を満たしているとき$T\subset S$と表します.よって,$T\subset T^*$は$D(T)\subset D(T^*)$かつ$Tf=T^*f$ ($f\in D(T)$)が成り立つということを述べてます.
Stoneの定理
準備ができたので,Stoneの定理を紹介します.
なお,定理の名前は証明したMarshall Harvey Stone氏にちなみます.
[Stoneの定理] $\{T_{t}\}_{t\in\R}$を$B(\mathcal{H})$上の族とする.このとき,$\{T_{t}\}_{t\in\R}$がユニタリ群であるためには,$\mathcal{H}$上の自己共役作用素$A$が存在して,$T_{t}=e^{itA}$を満たすことが必要十分である.
言い換えれば,
- $\{T_{t}\}_{t\in\R}$がユニタリ群であれば,自己共役作用素$A$が存在して,$iA$が$\{T_{t}\}_{t\in\R}$の生成作用素となる
- $A$が自己共役作用素であれば,$iA$を生成作用素にもつ$C_0$群$\{T_{t}\}_{t\R}$が存在して,$\{T_{t}\}_{t\R}$はユニタリ群となる
というわけですね.
このStoneの定理の応用としては,自由Schrödinger発展作用素が挙げられます.
詳しくは,以下の記事を参照してください.
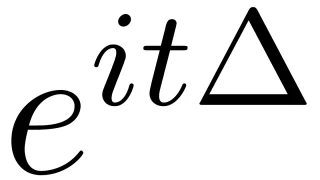
参考文献
以下は参考文献です.
関数解析
[黒田成俊 著/共立出版]
本書は関数解析の入門書です.
初学者に非常に読みやすく,多くの関数解析の授業でも教科書指定されることが多いテキストです.
関数解析において基本的なバナッハ空間,ヒルベルト空間の丁寧な解説から始まり,半群理論(ヒレ-吉田の定理)やコンパクト作用素など,関数解析の応用にまで触れられています.
証明が詳しく行間が少ないのも初学者にはありがたいところです(行間がなくはありませんが,理解できていれば埋められる程度なので,自分の理解を確かめるためにも自分で行間を埋める訓練は大切でしょう).
関数解析においてはリーマン積分ではなくルベーグ積分をメインに用いますが,それほどルベーグ積分を習熟していない人でも読み進められるように,巻末にルベーグの収束定理などルベーグ積分の重要事項がまとめられています.
この巻末の付録を参照すれば,ルベーグ積分を習得しつつ読み進めることができます.
また,3段階のレベルに分けて章末の演習問題が構成されており,自分の理解の確認と助けになります.
なお,本書については,以下の記事で書評としてまとめています.
本書の目次・必要な知識・良い点と気になる点・オススメの使い方などをレビューしています.



コメント