自由シュレディンガー(Schrödinger)方程式
\begin{align*}i\partial_t{u}(t,x)+\Delta u(t,x)=0\end{align*}
の初期値$u_0=u(0,x)$に対する解$u=e^{it\Delta}u_0$は基本解と呼ばれ,$L^pL^q$評価が成り立つのでした.
$L^pL^q$評価を用いると,シュレディンガー方程式を考える際に重要な評価であるストリッカーツ評価を証明することができます.
この記事では,Schrödinger方程式に関するストリッカーツ評価を紹介し,証明します.
一連の記事はこちら
【自由シュレディンガー方程式の基本解とユニタリ群】
【シュレディンガー方程式の分散性|基本解のLpLq評価の導出】
【シュレディンガー方程式のストリッカーツ評価の導出】←今の記事
ストリッカーツ評価のための準備
ストリッカーツ評価のためにいくつか準備をしましょう.
$L^pL^q$評価(復習)
まずは$L^pL^q$評価を確認しておきましょう.
[$L^{p}L^{q}$評価]$p\in[2,\infty]$と$u\in L^{q}(\R^{d})$に対して
\begin{align*}\|e^{it\Delta}u\|_{L^{p}(\R^{d})}
\le\bra{4\pi|t|}^{-\bra{\frac{d}{2}-\frac{d}{p}}}\|u\|_{L^{q}(\R^{d})}\end{align*}
が成り立つ.ただし,$q\in[1,2]$は$p$のヘルダー共役である:$1=\frac{1}{p}+\frac{1}{q}$.
$p=2$の場合と$p=\infty$の場合を直接証明し,$2<p<\infty$の場合はリース-トーリンの複素補間定理より成り立つという証明でした.この記事の本題のストリッカーツ評価の証明でも補間を用いるので意識しておくと良くでしょう.
時空ノルム
$\Omega$を可測集合とするとき,$L^p(\Omega)$ノルムは
\begin{align*}\|f\|_{L^p(\Omega)}:=\bra{\int_{\Omega}|f(x)|^p\,dx}^{1/p}\end{align*}
ですね.さらに$I\subset\R$を区間とするとき,$F:I\times\R^d\to\C$に対して,次のように時空ノルム$\|\cdot\|_{L^q(I;L^r)}$を定めます.
$q,r\ge1$とし,区間$I\subset\R$とする.可測関数$F:I\times\R^d\to\C$に対して,
\begin{align*}\|F\|_{L^q(I;L^r)}
:=&\nor{\|F\|_{L^{r}_{x}(\R^d)}}_{L^q_t(I)}
\\=&\brb{\int_{I}\bra{\int_{\R^d}|F(t,x)|^r\,dx}^{q/r}\,dt}^{1/q}\end{align*}
と定め,$\|F\|_{L^q(I;L^r)}<\infty$となる可測関数$F$全体の空間を$L^q(I;L^r(\R^d))$や$L^qL^r(I\times\R^d)$などと表す.
ハーディ-リトルウッド-ソボレフの不等式
ここではハーディ-リトルウッド-ソボレフの不等式を説明しますが,その前に便利な不等式の記号$\lesssim$を定義しておきます.
集合$X$上の関数$p,q:X\to\R$が
\begin{align*}\exi C>0\ \mrm{s.t.}\ \all x\in X\ p(x)\le Cq(x)\end{align*}
を満たすとき$p(x)\lesssim q(x)$と表す.
続けて不等式を行うときには,$p(x)\le Cq(x)$の$C$は変化していくことは多いですが,その度に$C_1,C_2,\dots$と新しい文字を導入するのは面倒です.
そのような場合には,不等式$\lesssim$を使えば,新たな定数を導入することなく不等式を続けて書くことができます.
$\lesssim$を使うかどうかは著者の好みによるところが大きいです.解析学では評価する際の定数倍が変化していく場合でも,同じ文字$C$を使い続けることもよくあります.
[ハーディ-リトルウッド-ソボレフの不等式]$p,q\in(1,\infty)$, $s\in(0,\frac{d}{p})$は$\frac{1}{q}=\frac{1}{p}-\frac{s}{d}$を同時に満たすとする.このとき,$f \in L^{p}(\R^{d})$に対して,
\begin{align*}\nor{\int_{\R^d}\frac{f(y)}{|x-y|^{d-s}}\,dy}_{L^q_x(\R^{d})}\lesssim\|f\|_{L^p(\R^{d})}\end{align*}
が成り立つ.
ストリッカーツ評価
ストリッカーツ評価は
- $\nor{e^{it\Delta}\phi}_{L^{q}_{t}(I;L^{r}_{x})}$
- $\nor{\dint_{t_0}^{t}e^{i(t-s)\Delta}F(s)\,ds}_{L^{q}_{t}(I;L^{r}_{x})}$
に関する評価ですが,これらの評価は好きな組$(q,r)$に対して成り立つわけではありません.
許容指数対
ストリッカーツ評価は組$(q,r)$が許容指数対である場合に成り立ちます.
$\frac{2}{q}+\frac{d}{r}=\frac{d}{2}$, $2<q\le\infty$を満たす組$(p,q)\in\R^2$は(ストリッカーツの)許容指数対(admissible pair)であるという.
また,組$(a,b)\in\R^2$に対して,ヘルダー共役の組$(a’,b’)$が許容指数対であるとき,$(a,b)$を双対許容指数対(dual-admissible pair)という.
$(q,r)$が許容指数対であるときは,$q$の範囲から自然に
- $d\ge3$のとき$2\le r<\frac{2d}{d-2}$
- $d=1,2$のとき$2\le r<\infty$
が得られます.このことから,$(q,r)$を許容指数対,$(a,b)$を双対許容指数対とすると,2点$(\frac{1}{r},\frac{1}{q})$,点$(\frac{1}{b},\frac{1}{a})$は下図の線分上に存在しますね.
$(\frac{1}{q},\frac{1}{r})$と$(\frac{1}{q’},\frac{1}{r’})$は点$(\frac{1}{2},\frac{1}{2})$に関して対称になりますね.
$d\ge3$のときストリッカーツ評価は$q=2(\iff r=\frac{2d}{d-2})$の場合にも成り立つことが示されており,このときの評価を端点評価といいます(Keel-Taoの定理).そのため,$(q,r)=(2,\frac{2d}{d-2})$も許容指数対に含めることもあります.
しかし,端点評価は別に証明が必要となるので,この記事では証明しません.
ストリッカーツ評価
準備ができたので,ストリッカーツ評価(Strichartz estimate)を紹介します.
[ストリッカーツ評価]$(q,r)$, $(a,b)\in\R^2$を許容指数対,$t_0\in\R$とし,区間$I\subset\R_{t}$は$t_0\in\overline{I}$を満たすとする.$\phi\in L^2_{x}(\R^{d})$と$F\in L^{a’}L^{b’}(I\times\R^{d})$に対して,次が成り立つ.
\begin{align*}&\nor{e^{it\Delta}\phi}_{L^{q}(I;L^r)}\lesssim\|\phi\|_{L^2}\quad\dots(\star),
\\&\nor{\int_{t_0}^{t}e^{i(t-s)\Delta}F(s)\,ds}_{L^q(I;L^r)}\lesssim\|F\|_{L^{a’}(I;L^{b’})}\quad\dots(\star\star)\end{align*}
ただし,$p\ge1$に対して,$p$のヘルダー共役を$p’$で表す.
不等式$(\star\star)$を言い換えれば,積分作用素
\begin{align*}L^{a’}_tL^{b’}_x(I\times\R^d)\to L^{q}_tL^{r}_x(I\times\R^d);F\longmapsto\int_{t_0}^{t}e^{i(t-s)\Delta}F(s)\,ds\end{align*}
が有界ということになります.この指数の関係を図で表せば下図のようになっています.
以下では不等式$(\star\star)$を補間を用いて証明します.この図をイメージできていれば補間の様子が分かりやすいでしょう.
証明(1つ目の不等式)
不等式$(\star)$を示す.任意の$g\in \mathcal{S}(I\times\R^{d})$に対して,
\begin{align*}\abs{\int_{I}\int_{\R^{d}}\bra{e^{it\Delta}\phi(x)}\overline{g(t,x)}\,dxdt}\lesssim\|g\|_{L^{q’}(I;L^{r’})}\|\phi\|_{L^2}\end{align*}
を示せば,双対性により$(\star)$が得られる.
$e^{it\Delta}$の$L^2(\R^d)$上の共役作用素が$e^{-it\Delta}$であることとヘルダーの不等式より,
\begin{align*}&\abs{\int_{I}\int_{\R^{d}}\bra{e^{it\Delta}\phi(x)}\overline{g(t)}\,dxdt}
\\=&\abs{\int_{I}\int_{\R^{d}}\phi(x)\overline{e^{-it\Delta}g(t,x)}\,dxdt}
=\abs{\int_{\R^{d}}\phi(x)\overline{\bra{\int_{I}e^{-it\Delta}g(t)\,dt}}\,dx}
\\\le&\|\phi(x)\|_{L^2_x}\nor{\overline{\int_{I}e^{-it\Delta}g(t)\,dt}}_{L^2_x}
=\|\phi\|_{L^2_x}\nor{\int_{I}e^{-it\Delta}g(t)\,dt}_{L^2_x}\end{align*}
が成り立つ.また,フビニ-トネリの定理,ヘルダーの不等式,$L^pL^q$評価,ハーディ-リトルウッド-ソボレフの不等式より
\begin{align*}&\nor{\int_{I}e^{-it\Delta}g(t)\,dt}_{L^2_x}^2
\\=&\int_{\R^d}\bra{\int_{I}e^{-is\Delta}g(s,x)\,ds}\overline{\bra{\int_{I}e^{-it\Delta}g(t,x)\,dt}}\,dx
\\=&\int_{I}\int_{I}\int_{\R^d}e^{-is\Delta}g(s,x)\overline{e^{-it\Delta}g(t,x)}\,dxdsdt
\\=&\int_{I}\int_{I}\int_{\R^d}e^{i(t-s)\Delta}g(s,x)\overline{g(t,x)}\,dxdsdt
\\\le&\int_{I}\bra{\int_{I}\nor{e^{i(t-s)\Delta}g(s)}_{L^r_x}\,ds}\nor{\overline{g(t)}}_{L^{r’}_x}\,dsdt
\\\lesssim&\int_{I}\bra{\int_{I}|t-s|^{-(\frac{d}{2}-\frac{d}{r})}\|g(s)\|_{L^{r’}_x}\,ds}\nor{g(t)}_{L^{r’}_x}\,dt
\\\le&\nor{\int_{I}|t-s|^{-(\frac{d}{2}-\frac{d}{r})}\|g(s)\|_{L^{r’}_x}\,ds}_{L^{q}_t}\|g\|_{L^{q’}(I;L^{r’})}
\\\lesssim&\|g\|_{L^{q’}(I;L^{r’})}^2\end{align*}
が成り立つから,双対性より不等式$(\star)$を得る.
証明(2つ目の不等式)
まずは$(q,r)=(a,b)$のときに不等式$(\star\star)$を示す.
ミンコフスキーの不等式,$L^pL^q$評価,ハーディ-リトルウッド-ソボレフの不等式から
\begin{align*}\nor{\int_{t_0}^{t}e^{i(t-s)\Delta}F(s)\,ds}_{L^{q}(I;L^r)}
=&\nor{\nor{\int_{t_0}^{t}e^{i(t-s)\Delta}F(s)\,ds}_{L^r_x}}_{L^q_t}
\\\le&\nor{\int_{t_0}^{t}\nor{e^{i(t-s)\Delta}F(s)}_{L^r_x}\,ds}_{L^q_t}
\\\lesssim&\nor{\int_{I}|t-s|^{-(\frac{d}{2}-\frac{d}{b})}\|F(s)\|_{L^{r’}_x}\,ds}_{L^{q}_t}
\\\lesssim&\|F\|_{L^{q’}(I;L^{r’})}
=\|F\|_{L^{a’}(I;L^{b’})}\quad\dots(\ast)\end{align*}
が成り立つ.
ここで,$r<b$のときと$b<r$のときの指数の関係を図で表せば,下図のようになっている.
よって,不等式
\begin{align*}\nor{\int_{t_0}^{t}e^{i(t-s)\Delta}F(s)\,ds}_{L^{\infty}(I;L^2)}\lesssim\|F\|_{L^{a’}(I;L^{b’})}\end{align*}
を示せば,上で示した不等式$(\ast)$との補間により$r<b$の場合が従い,
\begin{align*}\nor{\int_{t_0}^{t}e^{i(t-s)\Delta}F(s)\,ds}_{L^{a}(I;L^b)}\lesssim\|F\|_{L^1_{t}(I;L^2)}\end{align*}
を示せば,上で示した不等式$(\ast)$との補間により$b<r$の場合が従う.
[1]$r<b$の場合を示す.不等式$(\star)$の証明の後半と同様に\begin{align*}
&\nor{\int_{t_0}^{t}e^{i(t-s)\Delta}F(s)\,ds}_{L^2_x}^2
\\=&\anb{\int_{t_0}^{t}e^{i(t-s)\Delta}F(s)\,ds,\int_{t_0}^{t}e^{i(t-s’)\Delta}F(s’)\,ds’}_{L^2_x}
\\\le&\int_{I}\int_{I}\nor{e^{i(s’-s)\Delta}F(s)}_{L^b_x}\|F(s’)\|_{L^{b’}_x}\,dsds’
\\\le&\int_{I}\bra{\int_{I}|s’-s|^{-(\frac{d}{2}-\frac{d}{b})}\|F(s)\|_{L^{b’}_x}\,ds}\|F(s’)\|_{L^{b’}_x}\,ds’
\\\le&\nor{\int_{I}|s’-s|^{-(\frac{d}{2}-\frac{d}{b})}\|F(s)\|_{L^{b’}_x}\,ds}_{L^a_{s’}}\|F\|_{L^{a’}(I;L^{b’})}
\\\lesssim&\|F\|_{L^{a’}(I;L^{b’})}^2
\end{align*}
が成り立つ.よって,
\begin{align*}
\nor{\int_{t_0}^{t}e^{i(t-s)\Delta}F(s)\,ds}_{L^{\infty}(I;L^2)}
\lesssim&\nor{\|F\|_{L^{a’}_{t}(I;L^{b’})}}_{L^{\infty}_t}
\\=&\|F\|_{L^{a’}(I;L^{b’})}\quad\dots(\ast\ast)
\end{align*}
を得る.よって,$r<b$のときに成り立つことが分かった.
[2]$b<r$の場合を示す.$T_+:=\sup I$, $T_-:=\inf I$とする.\begin{align*}&\set{(s,t)\in\R^2}{t_0\le t\le T_+,t_0\le s\le t}
\\&\qquad=\set{(s,t)\in\R^2}{t_0\le s\le T_+,s\le t\le T_+},
\\&\set{(s,t)\in\R^2}{T_-\le t\le t_0,t\le s\le t_0}
\\&\qquad=\set{(s,t)\in\R^2}{T_-\le s\le t_0,T_-\le t\le s}\end{align*}
なので,任意の$g\in\mathcal{S}(I\times\R^{d})$に対して,$(\ast\ast)$を用いれば
\begin{align*}&\abs{\int_{I}\int_{\R^d}\bra{\int_{t_0}^{t}e^{i(t-s)\Delta}F(s,x)\,ds}\overline{g(t,x)}\,dxdt}
\\=&\abs{\int_{\R^d}\int_{I}\int_{t_0}^{t}F(s,x)\overline{e^{i(s-t)\Delta}g(t,x)}\,dsdtdx}
\\=&\left|\int_{\R^d}\int_{t_0}^{T_+}\int_{t_0}^{t}F(s,x)\overline{e^{i(s-t)\Delta}g(t,x)}\,dsdtdx\right.
\\&\quad-\left.\int_{\R^d}\int_{T_-}^{t_0}\int_{t}^{t_0}F(s,x)\overline{e^{i(s-t)\Delta}g(t,x)}\,dsdtdx\right|
\\\le&\left|\int_{\R^d}\int_{t_0}^{T_+}\overline{\bra{\int_{s}^{T_+}e^{i(s-t)\Delta}g(t,x)\,dt}}F(s,x)\,dsdx\right.
\\&\quad-\left.\int_{\R^d}\int_{T_-}^{t_0}\overline{\bra{\int_{T_-}^{s}e^{i(s-t)\Delta}g(t,x)\,dt}}F(s,x)\,dsdx\right|
\\\le&\abs{\int_{t_0}^{T_+}\int_{\R^d}\overline{\bra{\int_{s}^{T_+}e^{i(s-t)\Delta}g(t,x)\,dt}}F(s,x)\,dxds}
\\&\quad+\abs{\int_{T_-}^{t_0}\int_{\R^d}\overline{\bra{\int_{T_-}^{s}e^{i(s-t)\Delta}g(t,x)\,dt}}F(s,x)\,dxds}
\\\le&\int_{I}\nor{\int_{s}^{T_+}e^{i(s-t)\Delta}g(t,x)\,dt}_{L^2_x}\|F(s)\|_{L^2_x}\,ds
\\&\quad+\int_{I}\nor{\int_{T_-}^{s}e^{i(s-t)\Delta}g(t,x)\,dt}_{L^2_x}\|F(s)\|_{L^2_x}\,ds
\\\le&\nor{\int_{a}^{s}e^{i(s-t)\Delta}g(t)\,dt}_{L^\infty(I;L^2)}\|F\|_{L^1(I;L^2)}
\\&\quad+\nor{\int_{b}^{s}e^{i(s-t)\Delta}g(t)\,dt}_{L^\infty(I;L^2)}\|F\|_{L^1(I;L^2)}
\\\lesssim&\|g\|_{L^{a’}(I;L^{b’})}\|F\|_{L^1(I;L^2)}\end{align*}
を得る.したがって,双対性により,
\begin{align*}\nor{\int_{t_0}^{t}e^{i(t-s)\Delta}F(s,\cdot)\,ds}_{L^a(I;L^b)}
\lesssim\|F\|_{L^1(I;L^2)}\end{align*}
を得る.よって,$b<r$のときに成り立つことが分かった.

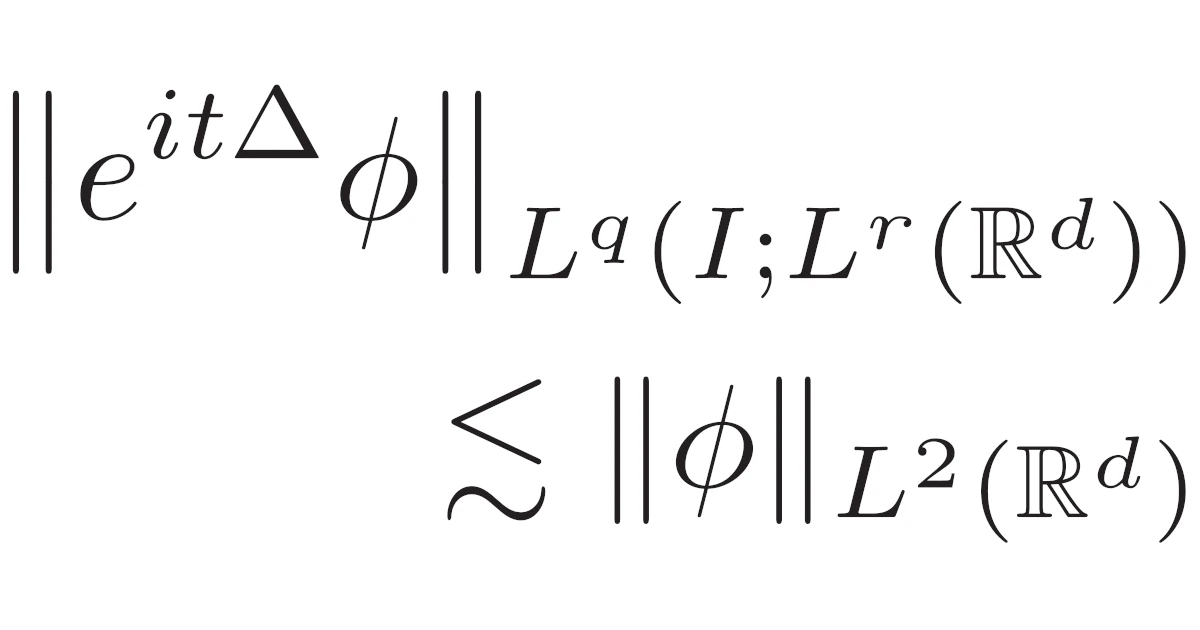
コメント