「非負値ルベーグ可測関数は非負値ルベーグ可測単関数で下から近似できる」という単関数列の近似定理がありました.
この定理を踏まえると,ルベーグ可測集合$A$上のルベーグ可測関数$f$をルベーグ可測単関数列$\{f_n\}$で近似したとき,
\begin{align*}\lim_{n\to\infty}\int_{A}f_n(x)\,dx=\lim_{n\to\infty}\int_{A}f(x)\,dx\end{align*}
となるように,非負値ルベーグ可測関数$f$に対するルベーグ積分を定義したいところですね.
この記事では
- 非負値可測関数のルベーグ積分
- 一般の非負値可測関数のルベーグ積分
を順に説明します.
「ルベーグ積分の基本」の一連の記事
- ルベーグ積分入門
- ルベーグ測度
- ルベーグ可測関数とルベーグ積分
非負値可測関数のルベーグ積分
単関数近似定理を確認して,非負値可測関数のルベーグ積分を定義しましょう.
単関数近似定理
非負値可測関数は単関数によって下から近似することができるのでした.
[単関数近似定理]可測集合$A$上の非負値可測関数$f$に対して,ある非負値単関数列$\{f_n\}$が存在して,
- 任意の$n$に対して$f_n$は可測関数
- $0\le f_1\le f_2\le\dots$
- $\lim\limits_{n\to\infty}f_n=f$
が成り立つ.
この単関数近似定理から,可測関数のルベーグ積分は単関数のルベーグ積分をもとにして考えるのが自然であるように思えますね.
非負値可測関数のルベーグ積分の定義
そこで,非負値可測関数のルベーグ積分を次のように定義します.
可測集合$A$上の非負値可測関数$f$と,$A$の分割
- $A=A_1\cup A_2\cup\dots\cup A_n$
- $A_i\cap A_j=\emptyset$ ($i\neq j$)
- $A_1,A_2,\dots,A_n$は可測集合
を考え,$\alpha_k:=\inf\limits_{x\in A_k}f(x)$とする.このとき,$A$の分割をさまざまに取ったときの和
\begin{align*}\alpha_1 m(A_1)+\alpha_2 m(A_2)+\dots+\alpha_n m(A_n)\quad\dots(*)\end{align*}
の集合の上限を$\dint_{A}f(x)\,dx$と表し,非負値可測関数$f$の$A$上のルベーグ積分という.
和$(*)$は単関数のグラフ$y=f_n(x)$と$x$軸の間の部分の面積に相当する量ですね.
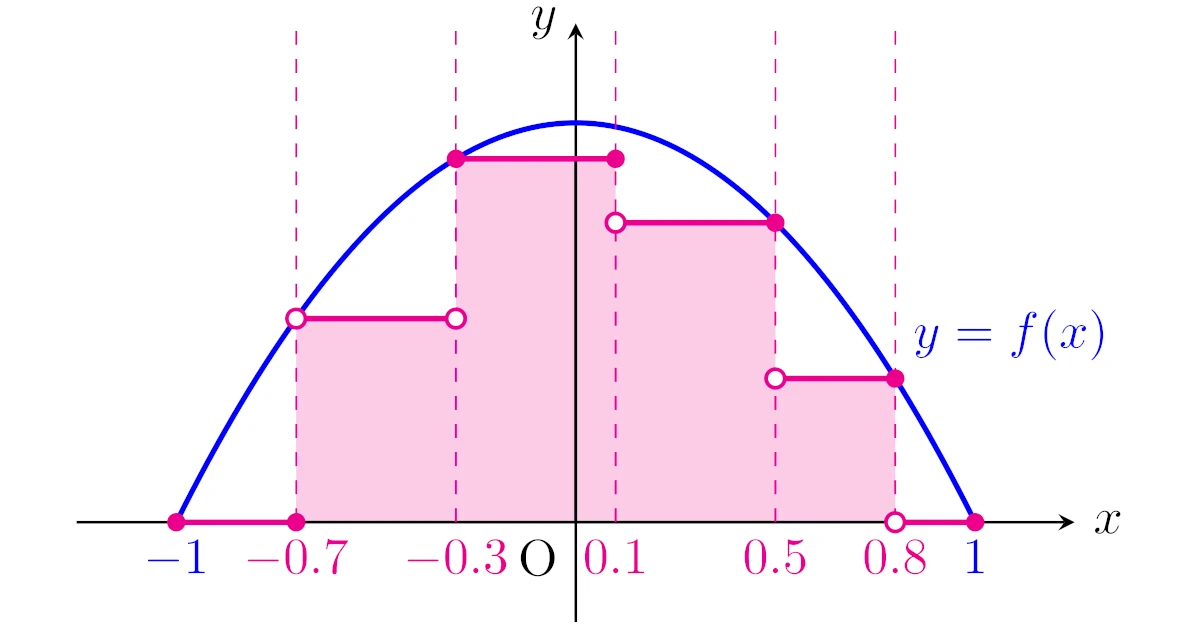
例えば,$A=[-1,1]$とし非負値関数$f:A\to\R;x\mapsto -x^2+1$を考えましょう.$n=6$で
\begin{align*}&A_1:=[-1,-0.7],\quad A_2:=(-0.7,-0.3),\quad A_3:=[-0.3,0.1],
\\&A_4:=(0.1,0.5],\quad A_5:=(0.5,0.8],\quad A_6:=(0.8,1]\end{align*}
とすると,和$(*)$は下図の色付き部分の面積になりますね.
$A$の分割はこの他にも無数に考えられ,もっと細かく分割していくと$y=f(x)$と$x$軸に囲まれる部分の面積に近付いていくことが見てとれます.
このように$A$をさまざまに分割してできる和$(*)$の上限を$f$のルベーグ積分と定めるわけですね.
このように定義すると,単関数近似定理による非負値可測関数$f$を下から近似する非負値単関数列$\{f_n\}$に関して,項別積分
\begin{align*}\lim_{n\to\infty}\int_{A}f_n(x)\,dx=\lim_{n\to\infty}\int_{A}f(x)\,dx\end{align*}
が成り立つことが証明できます.この証明には少し準備が必要なので,のちの記事で示します.
一般の可測関数のルベーグ積分
非負とは限らない一般の可測関数$f$のルベーグ積分は,$f\ge0$となるところと$f\le0$となるところに分けて定義されます.
正成分と負成分
$A\subset\R$とする.関数$f:A\to\R$に対して,
\begin{align*}f_+(x)=\max\{f(x),0\},\quad
f_-(x)=\max\{-f(x),0\}\end{align*}
で定まる関数$f_+,f_-:A\to\R$をそれぞれ$f$の正成分,負成分という.
つまり,
- 関数の負の部分を全て0にしたものが正成分
- 関数の正の部分を全て0にしてー1をかけたものが負成分
ですね.また,次の補題も思い出しておきましょう.
可測集合$A$上の可測関数$f$に対して,正成分$f_+$と負成分$f_-$はともに非負値可測関数である.
この補題から可測関数$f$の正成分$f_-$と負成分$f_+$には非負値可測関数のルベーグ積分が定義されることが分かりますね.
一般の可測関数のルベーグ積分の定義
一般の可測関数$f$のルベーグ積分は(正成分$f_+$のルベーグ積分)-(負成分$f_-$のルベーグ積分)で定義されます.
可測集合$A$上の可測関数$f$を考える.正成分$f_+$と負成分$f_-$の非負値可測関数のルベーグ積分について,
- $\int_{A}f_+(x)\,dx<\infty$
- $\int_{A}f_-(x)\,dx<\infty$
のいずれか一方を満たすとき,
\begin{align*}\int_{A}f_+(x)\,dx-\int_{A}f_-(x)\,dx\end{align*}
を$\dint_{A}f(x)\,dx$と表し,可測関数$f$の$A$上のルベーグ積分という.
また,(1), (2)の両方を満たすとき,すなわちルベーグ積分が有限の値をとるとき,$f$はルベーグ可積分関数という.
$f$の$A$上のルベーグ積分は$\dint_{A}f(x)\,m(dx)$や$\dint_{A}f(x)\,dm(x)$などと表すこともあります.
$\int_{A}f_+(x)\,dx$と$\int_{A}f_-(x)\,dx$がともに$\infty$の場合は$\infty-\infty$となって定義できないため,どちらか一方は$\infty$でない場合のみ定義するわけですね.



コメント