大雑把に言えば，添え字$m,n$が大きければ$a_n$と$a_m$の値がほとんど違わないような実数列$\{a_n\}$をコーシー列といいます．
この記事で説明するように実数列が収束列であることとコーシー列であることは同値であり，このことから実数列の収束を簡単に示せる場合があります．
この記事では
- コーシー列の定義
- コーシー列の性質
- コーシー列の応用例と注意点
を順に解説します．
「微分積分学の基本」の一連の記事
微分積分学の参考文献
以下は微分積分学に関するオススメの教科書です．
微分積分学（笠原晧司 著）
数学科など理論系の学生向けの微分積分学の入門書です．基本的な例から発展的な例まで扱われており，バランスの良い教科書です．
コーシー列の定義
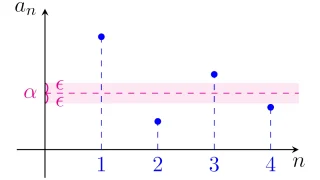
コーシー列の定義はε-N論法による実数列の収束の定義に似ているので，まずは実数列の収束の定義を復習しておきましょう．
実数列の収束（$\epsilon\text{-}N$論法）の定義の復習
実数列$\{a_n\}$が$\alpha\in\R$に収束するとは，任意の$\epsilon>0$に対して，ある$N\in\N$が存在して，
\begin{align*}n>N\Ra|a_n-\alpha|<\epsilon\end{align*}
が成り立つことをいう．また，このとき$\lim\limits_{n\to\infty}a_n=\alpha$や$a_n\to\alpha\ (n\to\infty)$などと表す．
言葉で説明すれば
- どんなに小さな正の数$\epsilon$を用意したとしても
- 十分大きな正の整数$N$をとれば
- $n>N$のとき$a_n$と$\alpha$の誤差$|a_n-\alpha|$を$\epsilon$よりも小さくできる
とき，実数列$\{a_n\}$は$\alpha$に収束するというわけですね．
コーシー列の定義
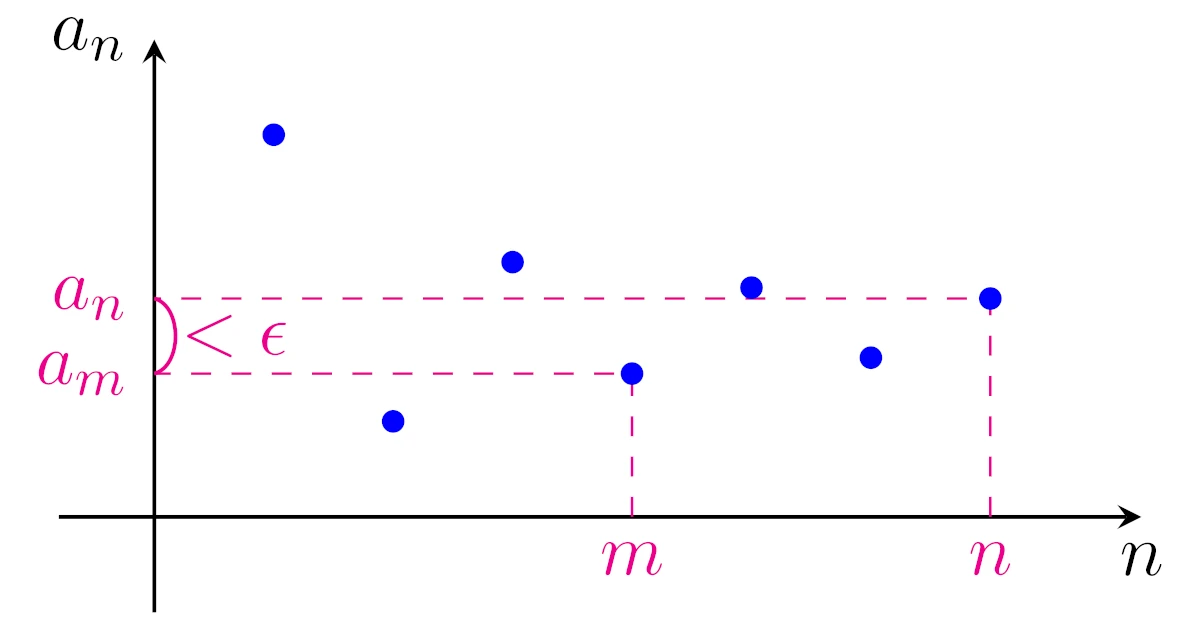
数列がコーシー列であるとは次のように定義されます．
実数列$\{a_n\}$がコーシー列（Cauchy sequence）であるとは，任意の$\epsilon>0$に対して，ある$N\in\N$が存在して，
\begin{align*}m,n>N\Ra|a_m-a_n|<\epsilon\end{align*}
が成り立つことをいう．
言葉で説明すれば
- どんなに小さな正の数$\epsilon$を用意したとしても
- 十分大きな正の整数$N$をとれば
- $m,n>N$のとき$a_m$と$a_n$の誤差$|a_m-a_n|$を$\epsilon$よりも小さくできる
とき，実数列$\{a_n\}$をコーシー列であるというわけですね．
「どこに近付いているか」という情報がなくてもコーシー列が定義される点が収束列との大きな違いで，のちに説明するようにこれがコーシー列の便利さに繋がっています．
コーシー列の性質
コーシー列がもつ基本性質をいくつか証明しておきましょう．
コーシー列の有界性
コーシー列の基本性質として，必ず有界であることが証明できます．
実数列$\{a_n\}$がコーシー列なら有界である．
$\{a_n\}$はコーシー列なので，ある$N\in\N$が存在して
\begin{align*}m,n>N\Ra|a_m-a_n|<1\quad\dots(*)\end{align*}
が成り立つから，$n>N$なら
\begin{align*}|a_{N+1}-a_n|<1\iff a_{N+1}-1<a_n<a_{N+1}+1\end{align*}
が成り立つ．よって，
\begin{align*}K:=&\max\{a_1,a_2,\dots,a_{N},a_{N+1}+1\},
\\L:=&\min\{a_1,a_2,\dots,a_{N},a_{N+1}-1\}\end{align*}
とおくと，任意の$n$に対して$L\le a_n\le K$が成り立つ．よって，実数列$\{a_n\}$は有界である．
$(*)$はコーシー列の定義で$\epsilon=1$として得られるものですね（$\epsilon$は任意なので，$\epsilon=1$としてもよいですね）．
添え字が$N$より大きいところで項は１より大きく違わないので，$n>N$なら$a_{n}$は$a_{N+1}$の誤差$\pm1$の範囲に収まっており有界です．また，$a_1,a_2,\dots,a_N$は有限個の項しかないので有界です．
このことから，コーシー列は全体で有界と言えるわけですね．
実数列は収束列ならコーシー列である
この記事の冒頭でも触れたように，実数列について
- 収束列であること
- コーシー列であること
は同値です．まずは収束列ならコーシー列であることを証明しましょう．
実数列$\{a_n\}$が収束列ならコーシー列である．
任意に$\epsilon>0$をとる．$\{a_n\}$は収束列なので，$\alpha:=\lim\limits_{n\to\infty}a_n$とおくと，ある$N\in\N$が存在して
\begin{align*}n>N\Ra|a_n-\alpha|<\frac{\epsilon}{2}\end{align*}
が成り立つ．よって，$m,n>N$なら三角不等式と併せて
\begin{align*}|a_m-a_n|=&|(a_m-\alpha)+(\alpha-a_n)|
\\\le&|a_m-\alpha|+|a_n-\alpha|<\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon\end{align*}
が成り立つ．よって，$\{a_n\}$はコーシー列である．
$m$, $n$が十分大きければ，$|a_m-\alpha|$, $|a_n-\alpha|$がどちらも十分に小さいことを利用して証明していますね．
この命題の証明には実数の性質を使っていないので，一般の距離空間上の点列に対しても同様の主張が成り立ちます．
実数列はコーシー列なら収束列である
先ほど証明したコーシー列の有界性にボルツァーノ-ワイエルシュトラスの定理を併せることで，実数列が逆にコーシー列なら実数に収束することを証明することができます．
実数列$\{a_n\}$がコーシー列なら収束列である．
任意に$\epsilon>0$をとる．コーシー列の定義より，ある$N_1\in\N$が存在して
\begin{align*}m,n>N_1\Ra|a_m-a_n|<\frac{\epsilon}{2}\quad\dots(*)\end{align*}
が成り立つ．上で示した補題よりコーシー列$\{a_n\}$は有界だから，ボルツァーノ-ワイエルシュトラスの定理より$\{a_n\}$の収束部分列$\{a_{n_k}\}_k$が存在する．
ここで$\alpha:=\lim\limits_{k\to\infty}a_{n_k}$とおく．このとき，ある$N_2\in\N$が存在して
\begin{align*}k>N_2\Ra|a_{n_k}-\alpha|<\frac{\epsilon}{2}\quad\dots(**)\end{align*}
が成り立つ．よって，$N:=\max\{N_1,N_2\}$とおけば，$n>N$のとき三角不等式と併せて
\begin{align*}|a_{n}-\alpha|=&|(a_n-a_{n_{N+1}})-(a_{n_{N+1}}-\alpha)|
\\&\le|a_n-a_{n_{N+1}}|+|a_{n_{N+1}}-\alpha|
\\&<\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon\end{align*}
が成り立つ．よって，$\{a_n\}$は収束列である．ただし，最後の不等号＜においては
- 第１項では$n,n_{N+1}>N\ge N_1$より$(*)$
- 第２項では$n_{N+1}>N\ge N_2$より$(**)$
を用いた．
$m,n$が十分大きければ，$|a_m-\alpha|$, $|a_n-\alpha|$がどちらも十分に小さいことを利用して証明していますね．
この定理の証明には実数の性質（ボルツァーノ-ワイエルシュトラスの定理）を使っているので，一般の距離空間上の点列に対しては成り立つとは限りません．
コーシー列の応用例と注意点
実数列についてコーシー列であることと収束列であることが同値なら，なぜわざわざコーシー列を定義する必要があるのか疑問に思う人がいるかもしれません．
しかし，実はコーシー列は次のような問題に応用することができます．
極限値が分からなくてもコーシー列であることが証明できる例
一般項$a_n=\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dots+\dfrac{1}{n^2}$の実数列$\{a_n\}$が収束することを示せ．
もし収束列であることを直接示そうとすると，極限値$\alpha$を見つけてきて$|a_n-\alpha|$を考える必要があります．
一方，コーシー列は極限値が分かっていなくてもよいのが，コーシー列の便利な点です．
数列$\{a_n\}$は実数列だからコーシー列であることを示せば収束することが分かる．
任意に$\epsilon>0$をとる．$m,n\in\N$を$m>n$とすると
\begin{align*}|a_m-a_n|=&\frac{1}{(n+1)^2}+\frac{1}{(n+2)^2}+\dots+\frac{1}{m^2}
\\\le&\frac{1}{n(n+1)}+\frac{1}{(n+1)(n+2)}+\dots+\dfrac{1}{(m-1)m}
\\<&\bra{\frac{1}{n}-\frac{1}{n+1}}+\bra{\frac{1}{n+1}-\frac{1}{n+2}}+\dots+\bra{\frac{1}{m-1}-\frac{1}{m}}
\\=&\frac{1}{n}-\frac{1}{m}<\frac{1}{n}\end{align*}
が成り立つ．よって，$N=\lceil{\frac{1}{\epsilon}}\rceil$とおくと，$m,n>N$なら
\begin{align*}|a_m-a_n|<\max\brb{\frac{1}{n},\frac{1}{m}}<\frac{1}{N}<\epsilon\end{align*}
となるから，$\{a_n\}$はコーシー列である．よって，$\{a_n\}$は収束する．
この解答例を読めば分かるように，コーシー列を使えば極限値のアタリがついていなくても収束することが証明できていますね．
実は極限$\lim\limits_{n\to\infty}\bra{\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dots+\dfrac{1}{n^2}}$を求める問題はバーゼル問題とよばれており，先人の努力により現在では
\begin{align*}\lim_{n\to\infty}\bra{\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dots+\dfrac{1}{n^2}}=\frac{\pi^2}{6}\end{align*}
であることが知られています．
しかし，$\abs{a_n-\frac{\pi^2}{6}}$を評価するのは大変ですから，上記のコーシー列を用いる解答のありがたみが分かりますね．
完備性と有理数列の注意点
ここまで説明してきた「実数列$\{a_n\}$がどんなコーシー列でも実数の極限値をもつ」という性質を実数全部の集合$\R$の完備性（completeness）といいます．
一方，実は有理数全部の集合$\Q$は完備性をもちません．すなわち，有理数列$\{a_n\}$がコーシー列であっても有理数の極限値をもつとは限りません．
実際，数列$\{a_n\}$の第$n$項を「$\sqrt{2}$の小数第$n$を切り捨ててできる実数」とすると，
\begin{align*}a_1=1,\ a_2=1.4,\ a_3=1.41,\ a_4=1.414,\dots\end{align*}
と全ての項が有理数となるので$\{a_n\}$は有理数列です．しかし，この極限$\lim\limits_{n\to\infty}a_n=\sqrt{2}$は有理数ではありませんね．
このように，収束する有理数列$\{a_n\}$がコーシー列だからといっても，極限$\lim\limits_{n\to\infty}a_n$は有理数とは限らないことに注意してください．
コメント