単調有界実数列の収束定理｜漸化式を解かずに極限を求める方法

次の問題を考えましょう．

［問題１］初項$a_{1}=\sqrt{2}$で漸化式

\begin{align*}a_{n+1}=\sqrt{2a_{n}}\end{align*}

を満たす数列$\{a_{n}\}$は収束するか？収束するなら極限値$X=\lim\limits_{n\to\infty}a_{n}$を求めよ．

漸化式を解くと

\begin{align*}a_n=2^{1-(1/2^{n})}\end{align*}

となるので，単純に極限をとって$X=\lim\limits_{n\to\infty}a_{n}=2$となります．

しかし，一般に漸化式は解けるとは限らないので，漸化式が解けない場合には別の方法が必要になります．

そのような方法のひとつに単調有界実数列の収束定理を用いる解法があります．

この記事では

単調有界実数列の収束定理と具体例
単調有界実数列の収束定理の証明

を順に説明します．

「微分積分学の基本」の一連の記事

実数・実数列の性質

微分積分学の参考文献
1. 微分積分学（笠原晧司著）
単調有界実数列の収束定理と具体例
1. 具体例
2. 収束することの重要性
単調有界実数列の収束定理の証明
補足（漸化式を変形して解く方法）

微分積分学の参考文献

以下は微分積分学に関するオススメの教科書です．

微分積分学（笠原晧司著）

数学科など理論系の学生向けの微分積分学の入門書です．基本的な例から発展的な例まで扱われており，バランスの良い教科書です．

単調有界実数列の収束定理と具体例

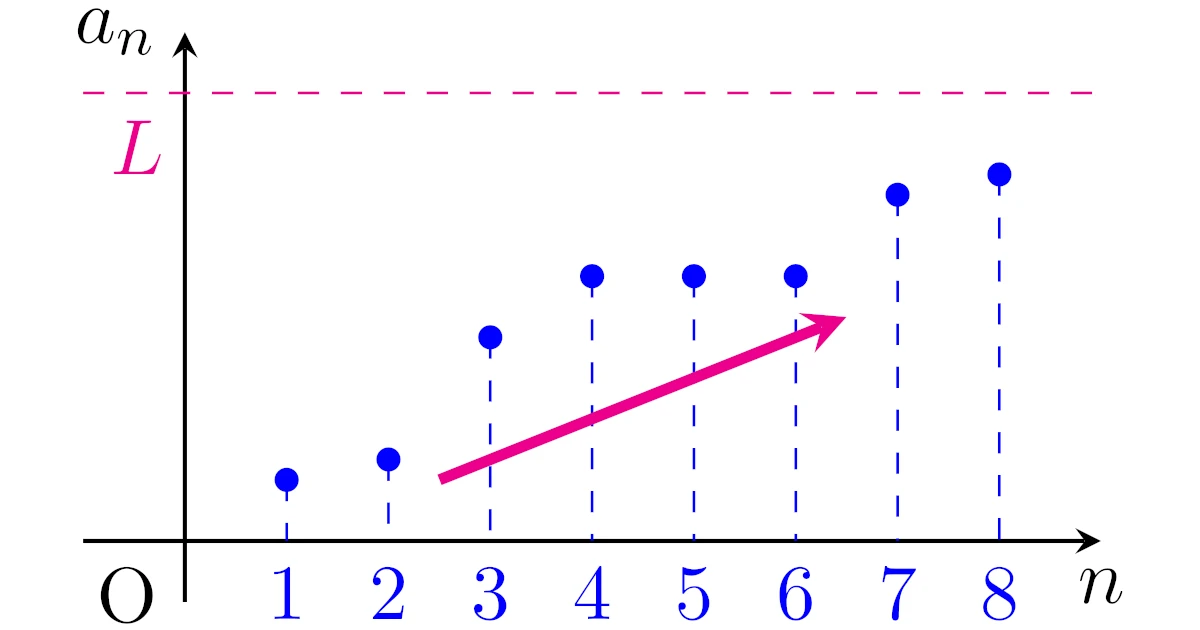
単調有界実数列の収束定理とは「実数列$\{a_n\}$が

$a_1\le a_2\le a_3\le\dots$となっている（広義単調増加）
ある$L>0$が存在して，任意の$n$に対して$a_n\le L$となる（上に有界）

という条件を満たすなら，どこかに収束するしかない」という定理です．

［単調有界実数列の収束定理］上に有界で広義単調増加する実数列は極限値をもつ．

\begin{tikzpicture}[scale=1.5]
\coordinate[label=below left:$\mrm{O}$](O) at (0,0); %原点
\coordinate(xs) at (-0.5,0); %x軸最小
\coordinate(xl) at (4.5,0); %x軸最大
\coordinate(ys) at (0,-0.3); %y軸最小
\coordinate(yl) at (0,2.5); %y軸最大
\draw[->,>=stealth,semithick](xs)–(xl) node[below]{$n$}; %x軸
\draw[->,>=stealth,semithick](ys)–(yl) node[left]{$a_{n}$}; %y軸

\coordinate(a1) at (0.5*1,0.3); %点a1
\coordinate(a2) at (0.5*2,0.4); %点a2
\coordinate(a3) at (0.5*3,1); %点a3
\coordinate(a4) at (0.5*4,1.3); %点a4
\coordinate(a5) at (0.5*5,1.3); %点a5
\coordinate(a6) at (0.5*6,1.3); %点a6
\coordinate(a7) at (0.5*7,1.7); %点a7
\coordinate(a8) at (0.5*8,1.8); %点a8

\foreach\n in{1,2,…,8}\draw[blue,dashed] (a\n)–($(xs)!(a\n)!(xl)$)node[below]{$\n$};
\foreach\n in{1,2,…,8}\fill[blue] (a\n) circle(0.06/1.5);
\draw[magenta,dashed]($(xs)+(0,2.2)$)node[below right]{$L$}–($(xl)+(0,2.2)$);
\draw[magenta,->,>=stealth,ultra thick](1.25,0.3)–(3.25,1.1);
\end{tikzpicture}

同様に，下に有界で広義単調減少する実数列も極限値をもちます．

一般には単調収束定理と呼ばれることが多いですが，この記事ではどのような定理か分かりやすい「単調有界実数列の収束定理」と呼ぶことにします．

具体例

単調有界実数列の収束定理を用いて冒頭の［問題１]を解きましょう．

［問題１（再掲）］初項$a_{1}=\sqrt{2}$で漸化式

\begin{align*}a_{n+1}=\sqrt{2a_{n}}\end{align*}

を満たす数列$\{a_{n}\}$は収束するか？収束するなら極限値$X=\lim\limits_{n\to\infty}a_{n}$を求めよ．

ステップ１

任意の$n\in\N$に対して$a_{n}\le a_{n+1}\le2$が成り立つことを数学的帰納法により示す．

(i) $n=1$のときは

$a_{1}=\sqrt{2}$
$a_{2}=\sqrt{2\sqrt{2}}=\sqrt{2}\sqrt[4]{2}$

であることから$a_{n}\le a_{n+1}\le2$が成り立つ．

(ii) $n=k$のときに成り立つと仮定する．このとき，

\begin{align*}a_{k+2}-a_{k+1}=&\sqrt{2a_{k+1}}-\sqrt{2a_{k}}=\sqrt{2}\bra{\sqrt{a_{k+1}}-\sqrt{a_{k}}}\ge0\end{align*}

かつ

\begin{align*}2-a_{k+2}=2-\sqrt{2a_{k+1}}=\sqrt{2}\bra{\sqrt{2}-\sqrt{a_{k+1}}}\ge0\end{align*}

が成り立ち，$n=k+1$のときにも成り立つことが分かる．

(ii), (ii)より，実数列$\{a_n\}$は狭義単調増加し上に有界だから，単調有界実数列の収束定理より実数列$\{a_n\}$は収束する．

すなわち，極限値$X=\lim\limits_{n\to\infty}a_{n}$は存在する．

ステップ２

漸化式$a_{n+1}=\sqrt{2a_{n}}$の両辺で極限$n\to\infty$を考えて

\begin{align*}X=\sqrt{2X}\quad\dots(*)\end{align*}

である．両辺２乗して$X^{2}-2X=0$より$X=0,2$である．

$X>0$で$X=2$は方程式$(*)$を満たすから極限値$X=2$を得る．

このように，漸化式が与えられた数列の一般項を求めなくても，

極限値$X:=\lim\limits_{n\to\infty}a_{n}$の存在を示す
漸化式で極限$n\to\infty$を考えて，$X$の方程式を解く

という手順で極限値を求められることがあります．

収束することの重要性

いまの解答例を読んで，「ステップ２だけで極限値が求まるので，ステップ１はなくてもいいのではないか？」という疑問を持った方もいらっしゃるかもしれません．

結論から言えば，ステップ１も必要なのですが，このことを理解するために次の問題を考えてみましょう．

［問題２］初項$a_{1}=1$で漸化式

\begin{align*}b_{n+1}=2b_{n}\end{align*}

を満たす数列$\{b_{n}\}$は収束するか？収束するなら極限値$Y=\lim\limits_{n\to\infty}b_{n}$を求めよ．

この問題を以下のように解いた人がいたらどうでしょうか？

［怪しい解答例］漸化式$b_{n+1}=2b_{n}+1$の両辺で極限$n\to\infty$を考えて

\begin{align*}Y=2Y+1\end{align*}

だから$Y=-1$となって，極限$Y=-1$を得る．

実際に［問題２］の数列$\{b_n\}$を漸化式から求めていくと，

\begin{align*}b_1=1,\ b_2=3,\ b_3=7,\ b_4=15,\dots\end{align*}

となり無限大に発散するはずですから，いまの［怪しい解答例］で得られた$Y=-1$という答えは誤りですね．

このように［怪しい解答例］で誤った答えが得られてしまったのは，実数列$\{b_n\}$の極限がそもそも存在していないにも関わらず，漸化式の両辺で極限$n\to\infty$を考えたことが原因です．

つまり，漸化式で極限$n\to\infty$をとって何らかの解が得られたとしても，収束するかどうかが不明ならそれが実際の極限値であるとは限らないわけですね．

よって，上の［問題１］の解答でもステップ２に先立ってステップ１で極限が存在していることを示しておくことは大切なわけですね．

単調有界実数列の収束定理の証明

序盤で単調性と有界性を簡単に説明しましたが，ここできちんと定義しておきましょう．

実数列の単調性

実数列$\{a_{n}\}$に対して，

$a_1\le a_2\le a_3\le \dots$が成り立つとき，$\{a_{n}\}$は広義単調増加する
$a_1<a_2<a_3<\dots$が成り立つとき，$\{a_{n}\}$は狭義単調増加する

という．

\begin{tikzpicture}
\begin{scope}
\coordinate[label=below left:$\mrm{O}$](O) at (0,0); %原点
\coordinate(xs) at (-0.5,0); %x軸最小
\coordinate(xl) at (4.5,0); %x軸最大
\coordinate(ys) at (0,-0.3); %y軸最小
\coordinate(yl) at (0,2.5); %y軸最大
\draw[->,>=stealth,semithick](xs)–(xl) node[below]{$n$}; %x軸
\draw[->,>=stealth,semithick](ys)–(yl) node[left]{$a_{n}$}; %y軸
\coordinate(a1) at (0.5*1,0.3); %点a1
\coordinate(a2) at (0.5*2,0.5); %点a2
\coordinate(a3) at (0.5*3,1.2); %点a3
\coordinate(a4) at (0.5*4,1.5); %点a4
\coordinate(a5) at (0.5*5,1.5); %点a5
\coordinate(a6) at (0.5*6,1.5); %点a6
\coordinate(a7) at (0.5*7,2); %点a7
\coordinate(a8) at (0.5*8,2.3); %点a8

\foreach\n in{1,2,3,6,7,8}\draw[blue,dashed] ($(ys)!(a\n)!(yl)$)–(a\n)–($(xs)!(a\n)!(xl)$)node[below]{$\n$};
\foreach\n in{4,5}\draw[blue,dashed] (a\n)–($(xs)!(a\n)!(xl)$)node[below]{$\n$};
\foreach\n in{1,2,…,8}\fill[blue] (a\n) circle(0.06);
\draw[magenta,->,>=stealth,ultra thick](1.25,0.3)–(3.25,1.3);
\draw[magenta,->,>=stealth](2.1,1.65)–(2.95,1.65);
\draw[magenta]($(1.25,0.3)!0.5!(3.25,1.3)$)node[below]{(1)};
\end{scope}

\begin{scope}[xshift=5.7cm]
\coordinate[label=below left:$\mrm{O}$](O) at (0,0); %原点
\coordinate(xs) at (-0.5,0); %x軸最小
\coordinate(xl) at (4.5,0); %x軸最大
\coordinate(ys) at (0,-0.3); %y軸最小
\coordinate(yl) at (0,2.5); %y軸最大
\draw[->,>=stealth,semithick](xs)–(xl) node[below]{$n$}; %x軸
\draw[->,>=stealth,semithick](ys)–(yl) node[left]{$a_{n}$}; %y軸
\coordinate(a1) at (0.5*1,0.3); %点a1
\coordinate(a2) at (0.5*2,0.5); %点a2
\coordinate(a3) at (0.5*3,1.2); %点a3
\coordinate(a4) at (0.5*4,1.4); %点a4
\coordinate(a5) at (0.5*5,1.6); %点a5
\coordinate(a6) at (0.5*6,1.9); %点a6
\coordinate(a7) at (0.5*7,2); %点a7
\coordinate(a8) at (0.5*8,2.3); %点a8

\foreach\n in{1,2,…,8}\draw[blue,dashed] ($(ys)!(a\n)!(yl)$)–(a\n)–($(xs)!(a\n)!(xl)$)node[below]{$\n$};
\foreach\n in{1,2,…,8}\fill[blue] (a\n) circle(0.06);
\draw[magenta,->,>=stealth,ultra thick](1.25,0.3)–(3.25,1.3);
\draw[magenta]($(1.25,0.3)!0.5!(3.25,1.3)$)node[below]{(2)};
\end{scope}
\end{tikzpicture}

広義と狭義の違いは

$a_n=a_{n+1}$となってもよいのが広義
$a_n=a_{n+1}$なってはならないのが狭義

というわけですね．よって，狭義単調増加であれば広義単調増加でもありますね．

単調減少についても同様に，

$a_1\ge a_2\ge a_3\ge \dots$が成り立つとき，$\{a_{n}\}$は広義単調減少する
$a_1>a_2>a_3>\dots$が成り立つとき，$\{a_{n}\}$は狭義単調減少する

といいます．

実数列の有界性

実数列$\{a_{n}\}$に対して，ある$L>0$が存在して，全ての$n$に対して$a_{n}\le L$が成り立つとき，$\{a_{n}\}$は上に有界であるという．

\begin{tikzpicture}
\coordinate[label=below left:$\mrm{O}$](O) at (0,0); %原点
\coordinate(xs) at (-0.5,0); %x軸最小
\coordinate(xl) at (4.5,0); %x軸最大
\coordinate(ys) at (0,-0.3); %y軸最小
\coordinate(yl) at (0,2.5); %y軸最大
\draw[->,>=stealth,semithick](xs)–(xl) node[below]{$n$}; %x軸
\draw[->,>=stealth,semithick](ys)–(yl) node[left]{$a_{n}$}; %y軸

\coordinate(a1) at (0.5*1,0.3); %点a1
\coordinate(a2) at (0.5*2,0.7); %点a2
\coordinate(a3) at (0.5*3,1); %点a3
\coordinate(a4) at (0.5*4,1.3); %点a4
\coordinate(a5) at (0.5*5,1.1); %点a5
\coordinate(a6) at (0.5*6,1); %点a6
\coordinate(a7) at (0.5*7,1.6); %点a7
\coordinate(a8) at (0.5*8,0.9); %点a8

\foreach\n in{1,2,…,8}\draw[blue,dashed] (a\n)–($(xs)!(a\n)!(xl)$)node[below]{$\n$};
\foreach\n in{1,2,…,8}\fill[blue] (a\n) circle(0.06);
\draw[magenta,dashed]($(xs)+(0,2.2)$)node[below right]{$L$}–($(xl)+(0,2.2)$);
\end{tikzpicture}

実数列$\{a_{n}\}$の項全部の集合$\{a_{1},a_{2},a_{3},\dots\}$についての有界性と同じですね．

単調減少についても同様に，ある$S>0$が存在して，全ての$n$に対して$a_{n}\ge S$が成り立つとき，$\{a_{n}\}$は下に有界であるといいます．

また，上に有界かつ下に有界であるときは，単に有界であるといいます．

単調有界実数列の収束定理の証明

［単調有界実数列の収束定理（再掲）］上に有界で広義単調増加する実数列は極限値をもつ．

一般に実数列$\{a_{n}\}$の項全部の集合$\{a_{1},a_{2},a_{3},\dots\}$の上限を$\sup{a_n}$と表します．

このとき，実数列は単調増加なので収束するなら極限値は$\sup{a_n}$となりそうですね．この考え方をもとに証明しましょう．

上に有界かつ広義単調増加する実数列$\{a_{n}\}$を考える．実数列$\{a_{n}\}$が$\alpha:=\sup{a_n}$に収束することを示す．

任意に$\epsilon>0$をとる．このとき，上限$\sup$の性質から

\begin{align*}\alpha-\epsilon<a_{N}\le\alpha\end{align*}

となる$N\in\N$が存在する．

また，実数列$\{a_{n}\}$は広義単調増加するから，$n>N$なら

\begin{align*}\alpha-\epsilon<a_{n}\le\alpha
\iff&-\epsilon<a_{n}-\alpha\le0
\\\Ra\ &|a_{n}-\alpha|<\epsilon\end{align*}

が成り立つ．よって，ε-N論法の定義より，実数列$\{a_{n}\}$は収束する．

同様に考えれば，次が成り立つことも分かりますね．

［単調有界実数列の収束定理］下に有界で広義単調減少する実数列は極限値をもつ．

補足（漸化式を変形して解く方法）

この記事のテーマとはズレますが，実際に漸化式を変形することでも極限が得られるので，この解法でも極限値$X=2$が得られることを確認しておきましょう．

［問題１（再掲）］漸化式$a_{n+1}=\sqrt{2a_{n}}$を満たす初項$a_{1}=\sqrt{2}$の数列$\{a_{n}\}$の極限値$X=\lim\limits_{n\to\infty}a_{n}$が存在すれば求めよ．

任意の$n\in\N$に対して$a_{n}>0$が成り立つことを数学的帰納法により示す．

$n=1$のときは$a_n=a_1=1>0$なので成り立つ．

また，$n=k$のときに成り立つと仮定すると，$a_{k+1}=\sqrt{2a_{n}}>0$なので$n=k+1$でも成り立つ．

よって，漸化式の両辺で対数$\log_2$がとれて，$b_n=\log_{2}a_n$とおけば

\begin{align*}b_{n+1}=\frac{1}{2}+\frac{1}{2}b_n
\iff b_{n+1}-1=\frac{1}{2}(b_{n}-1)\end{align*}

である．よって，実数列$\{b_n-1\}$は公比$\dfrac{1}{2}$の等比数列なので，

\begin{align*}\lim_{n\to\infty}b_n-1=0
\iff\lim_{n\to\infty}a_n=2\end{align*}

を得る．

なお，$b_{n+1}-1=\frac{1}{2}(b_{n}-1)$をきちんと最後まで解くと

\begin{align*}b_{n}-1=\frac{1}{2^{n-1}}(b_{1}-1)
&\iff b_{n}=1-\frac{1}{2^{n}}
\\&\iff a_{n}=2^{1-(1/2^{n})}\end{align*}

となり，ここから$\lim\limits_{n\to\infty}a_n=2^{1-0}=2$ともできますね．

より素朴には

\begin{align*}a_n=2^{1/2}2^{1/4}\dots2^{1/2^n}=2^{(1/2)+(1/4)+\dots+(1/2^{n})}\end{align*}

なので，指数部分で等比数列の和の公式を用いて$a_n=2^{1-(1/2^{n})}$としても一般項が得られますね．

微分積分学の参考文献

微分積分学（笠原晧司 著）

単調有界実数列の収束定理と具体例

具体例

ステップ１

ステップ２

収束することの重要性

単調有界実数列の収束定理の証明

実数列の単調性

実数列の有界性

単調有界実数列の収束定理の証明

補足（漸化式を変形して解く方法）

コメント

微分積分学（笠原晧司著）