小学校では割り算を通して有理数を理解し，全ての有理数は数直線上に表せることを学びます．
中学校では$\sqrt{2}$のような無理数の存在を知り，無理数は有理数とは異なる数でも同じく数直線上に表せることを学びます．
ただし，中学校では$\sqrt{2}$が無理数であることの証明はしないことが多いです．
無理数を初めて学ぶ際には「有理数でない『数』を無理数という」と学びますが，そもそもここでいう「数」とはなんでしょうか？
この答えは実数ということになりますが，この実数の正体については中学校や高校ではおろか大学でも数学科のような一部の学部でしか学びません．
実は実数を定義するためには実数の連続性公理と呼ばれる性質がカギとなっています．実数の連続性公理はいくつかの同値な表し方があり，その中でメジャーなものとして上限性質と呼ばれるものがあります．
この記事では，実数の連続性公理がどのようなものか理解し，実数の正確な定義を説明します．
有理数と無理数
最初に有理数と無理数の基本事項を確認しておきましょう．
$\dfrac{m}{n}$ ($m$, $n$は整数，$n\neq0$)の形で表せる数を有理数（rational number）という．
厳密には整数環$(\Z,+,\times)$の乗法的部分集合$\Z\setminus\{0\}$による局所化によりできる商体を有理数体といい，有理数体の元を有理数と呼びますが，この記事では詳しくは説明しません．
ここで「実数の定義は？」という質問をしたとき，「実数の定義は有理数と無理数を併せたもの」と答えるのは誤答です．
これは無理数は実数と有理数をもとに次のように定義されるためです．
有理数でない実数を無理数 （irrational number）という．
つまり，無理数を定義するためには実数が先に定義されている必要があり，「実数の定義は有理数と無理数を併せたもの」とすると循環論法になってしまいます．
このことから，実数は無理数を用いない方法で定義することになります．
順序体
冒頭で説明した実数の連続性公理の１つの表し方である上限性質を説明する前に順序体を準備する必要があります．
順序体とは
集合$X$が順序体であるとは，簡単に言えば
- $X$で四則演算が適切にできて
- $X$の全ての元同士で順序が定まっていて
- $X$の演算と順序の相性がいい
ということをいいます．
身近な例を挙げれば，有理数全部の集合$\Q$は（自然な演算$+$, $\times$と順序$\le$で）順序体です．
つまり，有理数の四則演算の結果は有理数で交換法則などの良い性質を満たしますし，異なる有理数を２個とってくれば必ず大小関係があります．
さらに，詳しくは後ほど説明するように，$\Q$上の加法$+$，乗法$\times$と順序$\le$の相性がいいことも分かります．
以下では上記の３つの性質をひとつずつ説明していきますが，$\Q$をイメージするとどういうものか理解しやすいでしょう．
体
１つ目の「$X$で四則演算が適切にできて」をきちんとした言葉で述べるなら，「$X$に定まっている加法$+$と乗法$\times$で体となる」となります．
以下に体のきちんとした定義を書きますが，大雑把には体とは「加法$+$と乗法$\times$について良い性質が成り立っていて，「０で割る」以外の四則演算ができる集合」のことをいいます．
体の定義を理解していなくても，この記事を読み進めるには問題ありません．
集合$X$に２つの演算$+$, $\times$が定まっているとする．
[1] $(X,+)$が群 (group)であるとは，
- 任意の$a,b,c\in X$に対し，$(a+b)+c=a+(b+c)$が成り立つ
- ある$0\in X$が存在し，任意の$a\in X$に対し，$a+0=0+a=a$が成り立つ
- 任意の$a\in X$に対し，ある$a’\in X$が存在し，$a+a’=a’+a=0$が成り立つ
- 任意の$a,b\in X$に対し，$a+b=b+a$が成り立つ
を満たすことをいう．
[2] $(X,+,\times)$は環 (ring)であるとは，[1]に加えて
- 任意の$a,b,c\in X$に対し，$(a\times b)\times c=a\times (b\times c)$が成り立つ
- ある$1\in X$が存在し，任意の$a\in X$に対し，$a\times 1=1\times a=a$が成り立つ
- 任意の$a,b,c\in X$に対し，$a\times (b+c)=ab+ac$が成り立つ
を満たすことをいう．
[3] 環$(X,+,\times)$が体 (field)であるとは，[1], [2]に加えて
- 任意の$a,b\in X$に対し，$a\times b=b\times a$が成り立つ
- 任意の$a\in X\setminus\{0\}$に対し，任意の$a\in X$に対し，ある$a”\in X$が存在し，$a\times a”=a”\times a=1$が成り立つ
を満たすことをいう．
有理数全部の集合$\Q$は普通の加法$+$と乗法$\times$で体となるので，この意味で$\Q$を有理数体と呼ぶことも多いです．
全順序集合
２つ目の「$X$の全ての元同士で順序が定まっていて」をきちんとした言葉で述べるなら，「$X$に全順序$\le$が定まっている」となります．
以下に全順序のきちんとした定義を書きますが，大雑把には全順序とは「一列に並んだ大小関係」のことをいいます．
全順序の定義を理解していなくても，この記事を読み進めるには問題ありません．
集合$X$上の二項関係$R$が順序 (order)であるとは
- 任意の$a\in X$に対し，$aRa$が成り立つ
- $a,b,c\in X$が$aRb$かつ$bRc$を満たせば，$aRc$が成り立つ
- $a,b\in X$が$aRb$かつ$bRa$を満たせば，$a=b$が成り立つ
を満たすことをいう．このとき，$R$は$\le$と表すことが多く，$(X,\le)$を順序集合という．
以上に加えて，任意の$a,b\in X$に対して，$a\le b$または$b\le a$の少なくとも一方が必ず成り立つとき，$\le$を全順序といい$(X,\le)$を全順序集合という．
演算と順序の両立
３つ目の「$X$の演算と順序の相性がいい」をきちんとした言葉で述べるなら，「体$X$に定まっている加法$+$，乗法$\times$と全順序$\le$が両立する」となります．
演算と順序の両立の定義を理解していなくても，この記事を読み進めるには問題ありません．
体$(X,+,\times)$を考える．また，$X$に全順序$\le$が定まっているとする．このとき，加法$+$，乗法$\times$と全順序$\le$が両立するとは
- $a,b\in X$が$a\le b$を満たせば，任意の$c\in X$に対して$a+c\le b+c$が成り立つ
- $a,b\in X$が$0\le a$かつ$0\le b$を満たせば，$0\le ab$が成り立つ
を満たすことをいう．
順序体の定義
以上で定義したものを用いて，順序体は次のように定義されます．
[順序体] 集合$X$が順序体であるとは，次を満たすことをいう．
- $X$に定まっている加法$+$と乗法$\times$で体となる．
- $X$に全順序$\le$が定まっている．
- $X$の演算$+$, $\times$と順序$\le$が両立する．
順序体の名前の通り，「順序の定まっている体」 であって，演算と順序がそれぞれ勝手に定まってるわけではなく，両立する程度の相性を持っているというわけですね．
実数の連続性公理(上限性質)
実数の定義のカギとなる[実数の連続性公理]はいくつもの同値な表し方があります．
この記事ではその中でもメジャーな上限性質を説明します．
他の同値な表し方として有名なものはデデキント(Dedekind)の切断公理があります．
準備
上限性質を理解するためには，順序集合における
- 上に有界
- 上限
という２つの概念が必要です．
[上に有界] 全順序集合$X$において，$A\subset X$が上に有界であるとは，ある$m\in X$が存在して，任意の$a\in A$に対して
が成り立つことをいう．また，このような$m$を$A$の上界という．
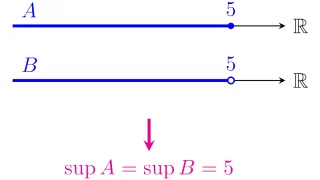
全順序集合$X$において，上に有界な$A\subset X$の上界のうち最小のものが存在すれば，その最小のものを$A$の上限 (supremum)といい，$\sup{A}$と表す．
例えば，有理数体$\Q$において
で$A,B\subset\Q$を定めると，$\sup{A}=2$ですが，$\sup{B}$は$\Q$において存在しません．
$\sup{B}$が$\Q$において存在しないことの詳しい証明は省略しますが，実数を定義すれば$\sqrt{2}$を用いて
となるので，実数の中では$\sup{B}=\sqrt{2}$となります．また，$\sqrt{2}$以上の有理数の最小値は存在しないので，$\Q$においては$\sup{B}$は存在しないわけですね．
上限について詳しくは以下の記事を参照してください．
上限性質
上に有界，上限の２つの定義から上限性質を定義することができます．
[上限性質] 集合$X$を全順序集合とする．「空でなく上に有界な$A\subset X$が必ず$X$上に上限$\sup{A}$をもつ」を満たすとき，$X$は上限性質を満たすという．
例えば，有理数体$\Q$は上限性質を満たしません．
なぜなら，上記の$B=\set{x\in\Q}{x^{2}<2}\subset\Q$は空でなく上に有界ですが，$\Q$上に上限$\sup{B}$をもたないからですね．
このように，空でなく上に有界であっても上限を持たないものが１つでもあれば上限性質は満たさないことになるわけですね．
実数の定義
ここまでで実数の定義をするための準備ができました．
[実数] 上限性質を満たす順序体を実数体といい，実数体の元を実数という．
また，実数体は$\R$と表すことが多い．
つまり，有理数体$\Q$のように順序体であり，それに加えて「空でなく上に有界な部分集合が必ず上限をもつくらいぎゅうぎゅうに詰まった集合」となっているとき，その順序体を実数体$\R$というわけですね．
実数における「上限性質」にはいくつもの同値な言い換えがあります．そのため，この実数の定義の「上限性質を満たす」の部分は他の同値な表し方で言い換えられることもあります．
そこで，上限性質を含めた同値な性質たちをまとめて実数の連続性公理といいます．
実数の構成
ただ，有理数の世界$\Q$に住む人の立場になってみると，「本当に『上限性質を満たす順序体』は存在するのか？」と不審に感じると思いませんか？
例えば，「三角形の２つの内角が$90^\circ$の三角形を超直角三角形という」と定義したとしても，三角形の内角の和は$180^\circ$ですから「超直角三角形」は存在しません．
このように「成り立たない定義」をしてしまうと，その定義を満たす対象が存在しないこともありうるわけですね．
ですから，$\Q$の部分集合として$B=\set{x\in\Q}{x^{2}<2}$のような$\Q$上に上限を持たない集合を知っているので，有理数の世界$\Q$に住む人たちとしては「成り立たない定義」になっている可能性を感じてしまうわけです．
しかし，安心してください．実は上限性質を満たす順序体を構成する方法が知られているので，きちんと見つけてくることで存在を証明することができます．
有理数体$\Q$を完備化して得られる順序体は実数体$\R$となる．
完備化とは「スカスカな順序集合」の隙間を埋めていくことで上限性質を持つ順序体を作る方法のことをいい，有理数体$\Q$の隙間を完備化で埋めていくことで上限性質を満たす順序体となること，つまり実数体$\R$となることが証明できます．
また，この他にも実数体$\R$の構成は知られていますが，どのように実数体$\R$を構成したとしても同一視できることが証明できます．
実数体$\R$は本質的にただ１つである．
参考文献
解析入門
[杉浦光男 著/東京大学出版会]
解析学の教科書としては非常に有名で，理論系で解析がしっかり必要となる人は持っておいてよいテキストです．
- 第１巻で１変数の微分積分学
- 第２巻で多変数の微分積分学
を扱っています．本書に対応した演習書「解析演習」も出版されています．
本書の特徴としては
- 数学的に厳密に書かれている
- 基本的な微分積分学の知識体系は網羅されている
の２点が挙げられます．
このため，辞書的に使う教科書という位置付けて持っている人も多いようです．
なお，この記事の内容は第１巻に載っています．
コメント