「ほとんど至る所」の定義・具体例・応用｜測度空間の零集合

ルベーグ積分において，例えば$\mathbb{R}$上の可積分関数$f,g$が零集合（測度０の集合）上のみで異なるとき，

$$\begin{array}{r}{\int }_{\mathbb{R}}f(x)dx={\int }_{\mathbb{R}}g(x)dx\end{array}$$

が成り立ちます．

一般の測度空間でも零集合上のことは無視しても結果に影響がないことはよくあり，零集合上でのみ例外であることを「ほとんど至る所で」と表現します．

この記事では

• 「ほとんど至る所で」の定義
• 「ほとんど至る所で」の具体例
• 「ほとんど至る所で」の応用

を順に説明します．

「ほとんど至る所で」の定義

測度空間上の零集合上のみで条件を満たさないことを次のように言います．

一般の測度空間$(X,\mathcal{F},\mu )$においては「ほとんど至る所で」と言いますが，確率空間においては次のように言います．

こちらは「起こり得るかもしれないが，確率としては０であるような条件$A(\omega )$」のことをいうわけですね．

「ほとんど至る所で」の具体例

以下では測度空間として$\mathbb{R}$上のルベーグ測度空間を考え，$m$をルベーグ測度とします．

具体例１（本質的に恒等的に値０をとる関数）

恒等的に値０をとる$\mathbb{R}$上の関数を${\mathbf{0}}_{\mathbb{R}}$で表し，$\mathbb{R}$上の関数$f$を

$$\begin{array}{r}f(x)=\{\begin{array}{ll}0& (x\ne 0)\\ 1& (x=0)\end{array}\end{array}$$

で定めます．

$f(x)={\mathbf{0}}_{\mathbb{R}}(x)$が成り立たないのは$x=0$のときに限るので，

$$\begin{array}{r}m(\left\{x\in \mathbb{R}\right|f(x)\ne 0_{\mathbb{R}}(x)\})=m(\{0\})=0\end{array}$$

となります．よって，$\mathbb{R}$上ほとんど至る所で$f(x)\ne 0_{\mathbb{R}}(x)$が成り立つということができ，これを

$$\begin{array}{r}f(x)={\mathbf{0}}_{\mathbb{R}}(x)\text{a.e.}x\in \mathbb{R}\end{array}$$

などと表すわけですね．

具体例２（ディリクレ関数）

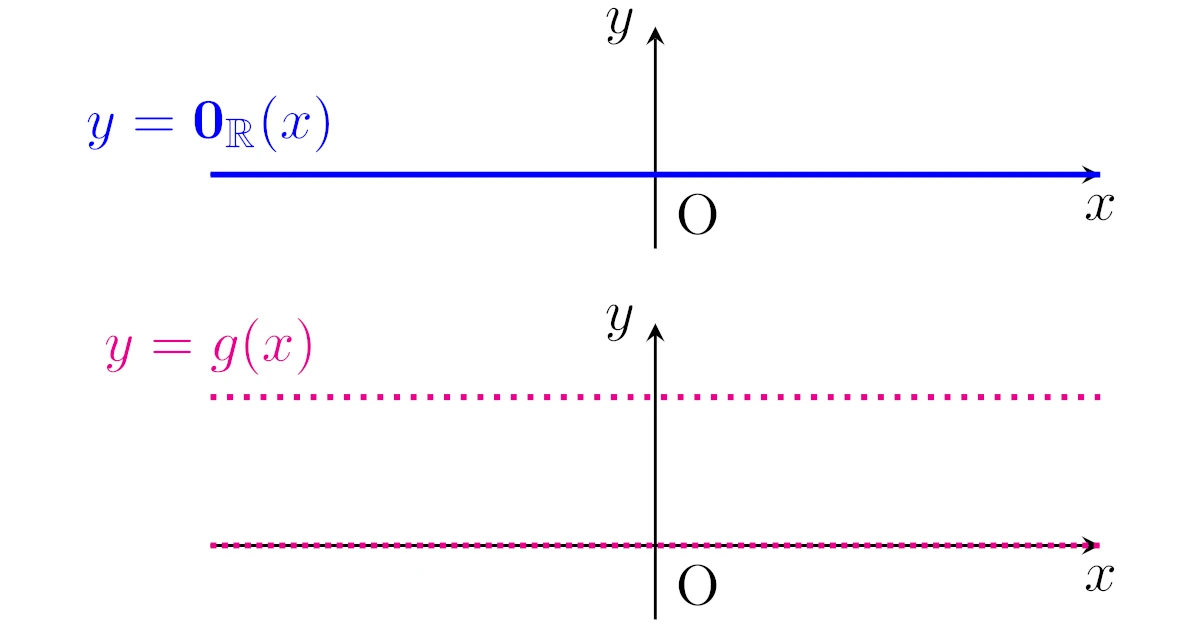
具体例１と同様に恒等的に値０をとる$\mathbb{R}$上の関数を${\mathbf{0}}_{\mathbb{R}}$で表します．また，ディリクレ（Dirichlet）関数$g$は

$$\begin{array}{r}g(x)=\{\begin{array}{ll}0& (x\in \mathbb{R}\setminus \mathbb{Q})\\ 1& (x\in \mathbb{Q})\end{array}\end{array}$$

で定まる$\mathbb{R}$上の関数のことをいいます．

有理数全部の集合$\mathbb{Q}$が零集合であることに注意すると，

$$\begin{array}{r}m(\left\{x\in \mathbb{R}\right|g(x)\ne {\mathbf{0}}_{\mathbb{R}}(x)\})=m(\mathbb{Q})=0\end{array}$$

となります．よって，$\mathbb{R}$上ほとんど至る所で$g(x)=0_{\mathbb{R}}(x)$が成り立つということができ，これを

$$\begin{array}{r}g(x)={\mathbf{0}}_{\mathbb{R}}(x)\text{a.e.}x\in \mathbb{R}\end{array}$$

などと表すわけですね．

具体例３（ほとんど至る所で各点収束）

$I:=[0,1]$とし，$I$上の関数列$\{h_n\}$を$h_n(x)={\displaystyle \frac{1}{1+x^n}}$で定めると，

$$\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{h}_n(x)=h(x):=\{\begin{array}{ll}1& (0\le x<1)\\ {\displaystyle \frac{1}{2}}& (x=1)\end{array}\end{array}$$

と各点収束します．

また，恒等的に値１をとる$I$上の関数を${\mathbb{I}}_I$で表しましょう．

このとき，

$$\begin{array}{r}m(\left\{x\in \mathbb{R}\right|h(x)\ne {\mathbb{I}}_I(x)\})=m(\{1\})=0\end{array}$$

となります．よって，$I$上ほとんど至る所で$\{h_n\}$は${\mathbb{I}}_I$に収束するということができ，これを

$$\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{h}_n(x)={\mathbb{I}}_I(x)\text{a.e.}x\in \mathbb{R}\end{array}$$

などと表すわけですね．

「ほとんど至る所で」の応用例

「ほとんど至る所」の応用例を考えましょう．

ルベーグ可積分関数はほとんど至る所で有限

普通，ルベーグ可測関数の終集合は拡大実数$\bar{\mathbb{R}}=\mathbb{R}\cup \{\pm \mathrm{\infty }\}$として考えることを思い出しておきましょう．

ほとんど至る所で等しい２つの関数の積分

同値関係による同一視

ほとんど至る所で等しい２つのルベーグ可測関数を関係付けると同値関係となります．

つまり，ほとんどいたるところ等しい関数たちをまとめてグループ分けできるということですね．

$p\ge 1$に対して「$p$乗ルベーグ可積分関数全部の集合でほとんど至る所で等しい関数たちを同一視してできる空間」は適切なノルムによりバナッハ空間（完備ノルム空間）になります．

この空間をルベーグ空間と呼び，$L^p$と表します．

ルベーグ空間$L^p$は解析学における基本的な関数空間のひとつとなっています．