$p\in[1,\infty)$のとき
が同型であることはよく知られており,これを$L^p$双対性といいます($p’$は$p$のヘルダー共役).
この同型について,任意の$v\in L^{p’}(\Omega)$に対して
\begin{align*}\|v\|_{L^{p’}(\Omega)}=\sup_{\|u\|_{L^{p}(\Omega)}=1}\abs{\int_{\Omega}u(x)v(x)\,dx}\end{align*}
が成り立ちます.また,混合ルベーグ空間$L^pL^q$でも同様の等式が成り立ち,これらの双対性の等式を用いる論法を双対性議論(duality argument)などといいます.
この記事では複素数値関数に対する$L^p$双対性,$L^pL^q$双対性を示します.
この記事では
- 準備(ヘルダーの不等式,ルベーグ空間,混合ルベーグ空間)
- $L^p$双対性とその証明
- $L^pL^q$双対性とその証明
を順に解説します.
準備(ヘルダーの不等式,ルベーグ空間,混合ルベーグ空間)
本題に入る前にヘルダーの不等式,ルベーグ空間$L^p$,混合ルベーグ空間$L^{p}L^{q}$を確認しておきましょう.
ヘルダーの不等式
$L^p$双対性の証明のベースとなるのはヘルダーの不等式です.
$\frac{1}{p}+\frac{1}{p’}=1$を満たす$p,p’\in[1,\infty]$はヘルダー共役であるという.ただし,$p=1$のときは$p’=\infty$,$p=\infty$のときは$p’=1$とみなす.
[ヘルダーの不等式]$p\in[1,\infty]$とする.ルベーグ可測集合$A\subset\R$上のルベーグ可測関数$f,g$に対して,不等式
\begin{align*}\int_{A}|f(x)g(x)|\,dx\le\|f\|_{p}\|g\|_{p’}\end{align*}
が成り立つ.ただし,$p’\in[1,\infty]$は$p$のヘルダー共役である.
実は実数値関数に対する$L^p$双対性($p\in(1,\infty)$)はヘルダーの不等式から簡単に証明でき,実際に$p\in(1,\infty)$の場合は以下の記事で証明しています.
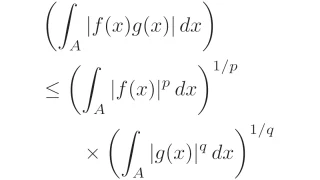
また,$p=1$のときは$q=\infty$となり,とくに性質を使うまでもなく
\begin{align*}\int_{A}|f(x)g(x)|\,dx\le\|f(x)\|_{\infty}\int_{A}|g(x)|\,dx=\|f(x)\|_{\infty}\|g\|_{1}\end{align*}
が得られ,この場合も含めてヘルダーの不等式ということもあります.以下,この$p=1$の場合も含めてヘルダーの不等式といいます.
ルベーグ空間$L^p$の定義
[ルベーグ空間]$\Omega\subset\R^N$をルベーグ可測集合とし,$p\in[1,\infty]$とする.このとき,ノルム
\begin{align*}\|u\|_{p}=\|u\|_{L^{p}(\Omega)}
:=\left\{\begin{aligned}
&\bra{\int_{\Omega}|u(x)|^{p}\,dx}^{1/p}&&(p\in[1,\infty))\\
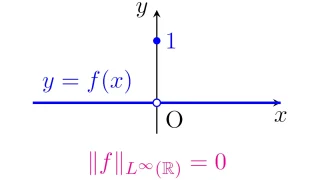
&\operatorname{ess\, sup}\limits_{x\in\Omega}|u(x)|&&(p=\infty)
\end{aligned}\right.\end{align*}
が有限なルベーグ可測関数$u$全部のノルム空間をルベーグ空間といい$L^p(\Omega)$と表す.
ルベーグ空間$L^p(\Omega)$は完備なノルム空間(バナッハ空間)となります.
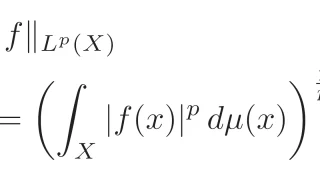
混合ルベーグ空間$L^pL^q$の定義
[混合ルベーグ空間]$i=1,2$に対して,$\Omega_i\subset\R^{N_i}$をルベーグ可測集合とし,$p,q\in[1,\infty]$とする.このとき,任意の$x_1\in\Omega_1$に対して$\|u(x_1,\cdot)\|_{L^q(\Omega)}<\infty$で,ノルム
\begin{align*}\|u\|_{p,q}=\|u\|_{L^{p}L^{q}(\Omega_1\times\Omega_2)}:=\brb{\int_{\Omega_1}\bra{\int_{\Omega_2}|u(x_1,x_2)|^{q}\,dx_2}^{p/q}\,dx_1}^{1/q}\end{align*}
が有限なルベーグ可測関数$u$全部のノルム空間を$L^{p}L^{q}(\Omega_1\times\Omega_2)$と表す.
混合ルベーグ空間$L^{p}L^{q}$は,例えば時間発展する非線形偏微分方程式で
- 空間$\R^n$に関して$L^{p}$
- 時間$\R$に関して$L^{q}$
である場合などに用います.
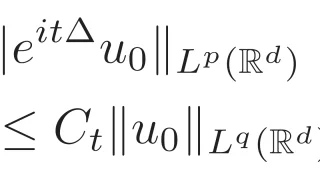
$L^p$双対性とその証明
複素数値関数に対する$L^p$双対性を示しましょう.
[$L^p$双対性]$\Omega\subset\R^N$をルベーグ可測集合とし,$p\in[1,\infty)$とする.このとき,任意の複素数値$v\in L^{p’}(\Omega)$に対して,
\begin{align*}\|v\|_{p’}=\sup_{\|u\|_{p}=1}\abs{\int_{\Omega}u(x)v(x)\,dx}\end{align*}
が成り立つ.ただし,$p’\in(1,\infty]$は$p$のヘルダー共役である.
$v=0$のときは両辺0で成り立つから,以下では$v\neq0$とする.
$\ge$の証明
ヘルダーの不等式より,任意の$v\in L^{p’}(\Omega)$に対して,
\begin{align*}\sup_{\|u\|_{p}=1}\abs{\int_{\Omega}u(x)v(x)\,dx}\le\sup_{\|u\|_{p}=1}\|u\|_{p}\|v\|_{p’}=\|v\|_{p’}\end{align*}
だから,あとは逆向きの不等式を示せばよい.
$p\in(1,\infty)$の場合の$\le$の証明
$p\in(1,\infty)$のときは$p’\in(1,\infty)$である.$\theta_{x}:=\arg v(x)$とし,$w:\Omega\to\C$を$w(x):=\dfrac{|v(x)|^{p’-1}}{\|v\|_{p’}^{p’/p}}e^{-i\theta_{x}}$で定める.
\begin{align*}\|w\|_{p}^{p}&=\int_{\Omega}|w(x)|^{p}\,dx
\\&=\frac{1}{\|v\|_{p’}^{p’}}\int_{\Omega}|v(x)|^{p(p’-1)}\,dx
\\&=\frac{1}{\|v\|_{p’}^{p’}}\int_{\Omega}|v(x)|^{p’}\,dx=1\end{align*}
だから
\begin{align*}&\sup_{\|u\|_{p}=1}\abs{\int_{\Omega}u(x)v(x)\,dx}
\\&\ge\abs{\int_{\Omega}w(x)v(x)\,dx}
=\abs{\frac{1}{\|v\|_{p’}^{p’/p}}\int_{\Omega}|v(x)|^{p’-1}e^{-i\theta_{x}}|v(x)|e^{i\theta_{x}}\,dx}
\\&=\frac{1}{\|v\|_{p’}^{p’/p}}\int_{\Omega}|v(x)|^{p’}\,dx
=\|v\|_{p’}^{p’-\frac{p’}{p}}
=\|v\|_{p’}\end{align*}
を得る.
$p=1$の場合の$\le$の証明
$p=1$のときは$p’=\infty$なので,$\|v\|_{\infty}<\infty$である.任意に$\epsilon>0$をとる.ルベーグ測度を$m$で表す.
本質的有界性の定義より,$0<m(\Omega_{\epsilon})<\infty$を満たすあるルベーグ可測集合$\Omega_{\epsilon}\subset\Omega$が存在して
\begin{align*}x\in\Omega_{\epsilon}\Ra|v(x)|>\|v\|_{\infty}-\epsilon\end{align*}
が成り立つ.このとき,$w:\Omega\to\C$を
\begin{align*}w(x):=\frac{\overline{v(x)}}{m(\Omega_{\epsilon})|v(x)|}\mathbb{I}_{\Omega_{\epsilon}}(x)\end{align*}
で定める.
\begin{align*}\|w\|_{p}=\int_{\Omega}|w(x)|\,dx=\frac{1}{m(\Omega_{\epsilon})}\int_{\Omega_{\epsilon}}\,dx=1\end{align*}
だから
\begin{align*}&\sup_{\|u\|_{p}=1}\abs{\int_{\Omega}u(x)v(x)\,dx}
\\&\ge\abs{\int_{\Omega}w(x)v(x)\,dx}
=\abs{\frac{1}{m(\Omega_{\epsilon})}\int_{\Omega_{\epsilon}}\frac{\overline{v(x)}v(x)}{|v(x)|}\,dx}
\\&=\frac{1}{m(\Omega_{\epsilon})}\int_{\Omega_{\epsilon}}|v(x)|\,dx
>\frac{1}{m(\Omega_{\epsilon})}\int_{\Omega_{\epsilon}}(\|v\|_{\infty}-\epsilon)\,dx
\\&=\|v\|_{\infty}-\epsilon\end{align*}
を得る.$\epsilon$の任意性から$\sup\limits_{\|u\|_{p}=1}\abs{\dint_{\Omega}u(x)v(x)\,dx}\ge\|v\|_{\infty}$が従う.
$p=1$の場合は関数$v\in L^{\infty}(\Omega)$をかける掛け算作用素$T_f:L^1(\Omega)\to L^1(\Omega)$の作用素ノルム$\|T_f\|$が$\|f\|_{\infty}$であることを示したのと同じことですね.
いまの定理では$\|u\|_{p}=1$なる$u$を動かして上限をとりましたが,$\|u\|_{p}\le1$なる$u$を動かして上限をとっても同じです.
$\Omega\subset\R^N$をルベーグ可測集合とし,$p\in[1,\infty)$とする.このとき,任意の複素数値関数$v\in L^{p’}(\Omega)$に対して,
\begin{align*}\|v\|_{p’}=\sup_{\|u\|_{p}\le1}\abs{\int_{\Omega}u(x)v(x)\,dx}\end{align*}
が成り立つ.ただし,$p’\in(1,\infty]$は$p$のヘルダー共役である.
ヘルダーの不等式より,任意の$v\in L^{p’}(\Omega)$に対して,
\begin{align*}\sup_{\|u\|_{p}\le1}\abs{\int_{\Omega}u(x)v(x)\,dx}\le\sup_{\|u\|_{p}\le1}\|u\|_{p}\|v\|_{p’}=\|v\|_{p’}\end{align*}
が成り立つ.一方,定理[$L^p$双対性]より,
\begin{align*}\|v\|_{p’}=\sup_{\|u\|_{p}=1}\abs{\int_{\Omega}u(x)v(x)\,dx}\le\sup_{\|u\|_{p}\le1}\abs{\int_{\Omega}u(x)v(x)\,dx}\end{align*}
が成り立つ.
$L^pL^q$双対性とその証明
複素数値関数に対する$L^pL^q$双対性を示しましょう.
[$L^{p}L^{q}$双対性]$i=1,2$に対して,$\Omega_i\subset\R^{N_i}$をルベーグ可測集合とし,$p,q\in[1,\infty)$とする.このとき,任意の複素数値$v\in L^{p’}L^{q’}(\Omega_1\times\Omega_2)$に対して,
\begin{align*}\|v\|_{p’,q’}=\sup_{\|u\|_{p,q}=1}\abs{\int_{\Omega_1}\int_{\Omega_2}u(x_1,x_2)v(x_1,x_2)\,dx_2dx_1}\end{align*}
が成り立つ.ただし,$p’,q’\in(1,\infty]$はそれぞれ$p$, $q$のヘルダー共役である.
$v=0$のときは両辺0で成り立つから,以下では$v\neq0$とする.また,$x:=(x_1,x_2)$とする.
$\ge$の証明
ヘルダーの不等式($\frac{1}{p}+\frac{1}{p’}=1$)より,任意の$v\in L^{p’}L^{q’}(\Omega_1\times\Omega_2)$に対して,
\begin{align*}&\sup_{\|u\|_{p,q}=1}\abs{\int_{\Omega_1}\bra{\int_{\Omega_2}u(x)v(x)\,dx_2}\,dx_1}
\\&\le\sup_{\|u\|_{p,q}=1}\int_{\Omega_1}\abs{\int_{\Omega_2}u(x)v(x)\,dx_2}dx_1
\\&\le\sup_{\|u\|_{p,q}=1}\int_{\Omega_1}\|u(x_1,\cdot)\|_{q}\|v(x_1,\cdot)\|_{q’}\,dx_1
\\&\le\sup_{\|u\|_{p,q}=1}\|u\|_{p,q}\|v\|_{p’,q’}=\|v\|_{p’,q’}\end{align*}
だから,あとは逆向きの不等式を示せばよい.
$\le$の証明
$\theta_{x}:=\arg v(x)$とする.任意の$u\in L^{p}L^{q}(\Omega_1\times\Omega_2)$に対して,$\phi\in L^{p}(\Omega_1)$と$g\in L^{\infty}L^{q}(\Omega_1\times\Omega_2)$を用いて,$u(x)=\phi(x_1)g(x)e^{-i\theta_x}$と表すとき,ヘルダーの不等式より
\begin{align*}\|u\|_{p,q}\le\|\phi\|_{p}\|g\|_{\infty,q}\end{align*}
が成り立つから,$\|\phi\|_{p}=1$かつ$\|g\|_{\infty,q}=1$ならば$\|u\|_{p,q}\le1$が成り立つ.よって,
\begin{align*}&\sup_{\|u\|_{p,q}=1}\abs{\int_{\Omega_1}\bra{\int_{\Omega_2}u(x)v(x)\,dx_2}\,dx_1}
\\&=\sup_{\|u\|_{p,q}\le1}\abs{\int_{\Omega_1}\bra{\int_{\Omega_2}u(x)v(x)\,dx_2}\,dx_1}
\\&\ge\sup_{\substack{\|\phi\|_{p}=1\\\|g\|_{\infty,q}=1}}\abs{\int_{\Omega_1}\bra{\int_{\Omega_2}\phi(x_1)g(x)e^{-i\theta_x}v(x)\,dx_2}\,dx_1}
\\&=\sup_{\substack{\|\phi\|_{p}=1\\\|g\|_{\infty,q}=1}}\abs{\int_{\Omega_1}\bra{\int_{\Omega_2}\phi(x_1)g(x)|v(x)|\,dx_2}\,dx_1}\quad\dots(*)\end{align*}
が成り立つ.最後の積分について
\begin{align*}&\abs{\int_{\Omega_1}\bra{\int_{\Omega_2}\phi(x_1)g(x)|v(x)|\,dx_2}\,dx_1}
\\&\le\int_{\Omega_1}\bra{\int_{\Omega_2}|\phi(x_1)||g(x)||v(x)|\,dx_2}\,dx_1\end{align*}
だから,$(*)$の上限は非負実数値関数$\phi$, $g$で考えれば十分である.また,トネリの定理と併せて
\begin{align*}&\sup_{\|u\|_{p,q}=1}\abs{\int_{\Omega_1}\bra{\int_{\Omega_2}u(x)v(x)\,dx_2}\,dx_1}
\\&\ge\sup_{\substack{\|\phi\|_{p}=1\\\phi\ge0}}\sup_{\substack{\|g\|_{\infty,q}=1\\g\ge0}}\int_{\Omega_1}\phi(x_1)\bra{\int_{\Omega_2}g(x)|v(x)|\,dx_2}\,dx_1\end{align*}
が成り立つ.
ここで,関数$H:\Omega_1\to\R$を
\begin{align*}H(x_1)=\sup_{\substack{\|g\|_{\infty,q}=1\\g\ge0}}\int_{\Omega_2}g(x)|v(x)|\,dx_2\end{align*}
で定める.各$x_1\in\Omega_1$に対して,$L^{q}(\Omega_2)$での双対性議論より$H(x_1)=\|v(x_1,\cdot)\|_{L^{q’}(\Omega_2)}$であり,ある非負値関数列$\{g_n\}\subset L^{\infty}L^{q}(\Omega_1\times\Omega_2)$が存在して,$g_1\le g_2\le g_3\le\dots$かつ
\begin{align*}H_n(x_1):=\int_{\Omega_2}g_n(x)|v(x)|\,dx_2\xrightarrow[]{n\to\infty}H(x_1)\end{align*}
が成り立つ.任意の非負実数値関数$\phi\in L^{p}(\Omega_1)$と$n\in\N$に対して,
\begin{align*}&\sup_{\substack{\|g\|_{\infty,q}=1\\g\ge0}}\int_{\Omega_1}\phi(x_1)\bra{\int_{\Omega_2}g(x)|v(x)|\,dx_2}\,dx_1
\ge\int_{\Omega_1}\phi(x_1)H_n(x_1)\,dx_1\end{align*}
なので,両辺(右辺)で極限$n\to\infty$をとると,ルベーグの単調収束定理より
\begin{align*}&\sup_{\substack{\|g\|_{\infty,q}=1\\g\ge0}}\int_{\Omega_1}\phi(x_1)\bra{\int_{\Omega_2}g(x)|v(x)|\,dx_2}\,dx_1
\ge\int_{\Omega_1}\phi(x_1)H(x_1)\,dx_1\end{align*}
が成り立つ.
以上と$L^{p}(\Omega_1)$での双対性議論を併せて,
\begin{align*}&\sup_{\|u\|_{p,q}=1}\abs{\int_{\Omega_1}\bra{\int_{\Omega_2}u(x)v(x)\,dx_2}\,dx_1}
\\&\ge\sup_{\substack{\|\phi\|_{p}=1\\\phi\ge0}}\int_{\Omega_1}\phi(x_1)H(x_1)\,dx_1
\\&=\|H\|_{L^{p’}(\Omega_1)}=\|v\|_{p’,q’}\end{align*}
を得る.

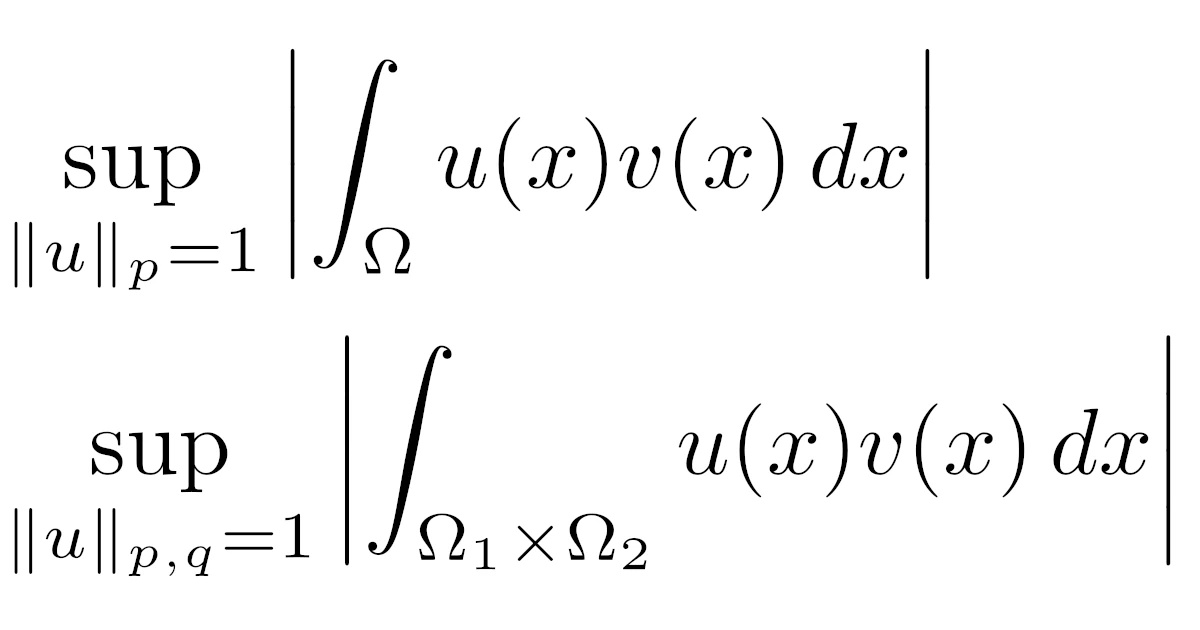
コメント