微分積分学の基本定理とその証明｜微分と積分の超重要な関係

理系大学１年生の多くが学ぶ微分積分学では，リーマン(Riemann)積分$\dint_{a}^{b}f(x)\,dx$を学びます．

リーマン積分$\dint_{a}^{b}f(x)\,dx$は微分を全く用いずに定義されるため，高校数学であまり扱わない不連続関数の積分にも対応することができます．

微分と無関係に定義されるリーマン積分ですが，「連続関数に対しては微分と積分が逆演算になっている」という微分積分学の基本定理が成り立ちます．

この微分積分学の基本定理を用いると，リーマン積分を簡単に計算することができます．

この記事では

不定積分
原始関数
微分積分学の基本定理

を順に説明します．

準備
1. 不定積分
2. 原始関数
微分積分学の基本定理
参考文献
1. 解析入門
2. 微分積分学

準備

微分積分学の基本定理を説明するために，不定積分と原始関数が必要なので，まずはこれらの定義を確認しておきましょう．

不定積分

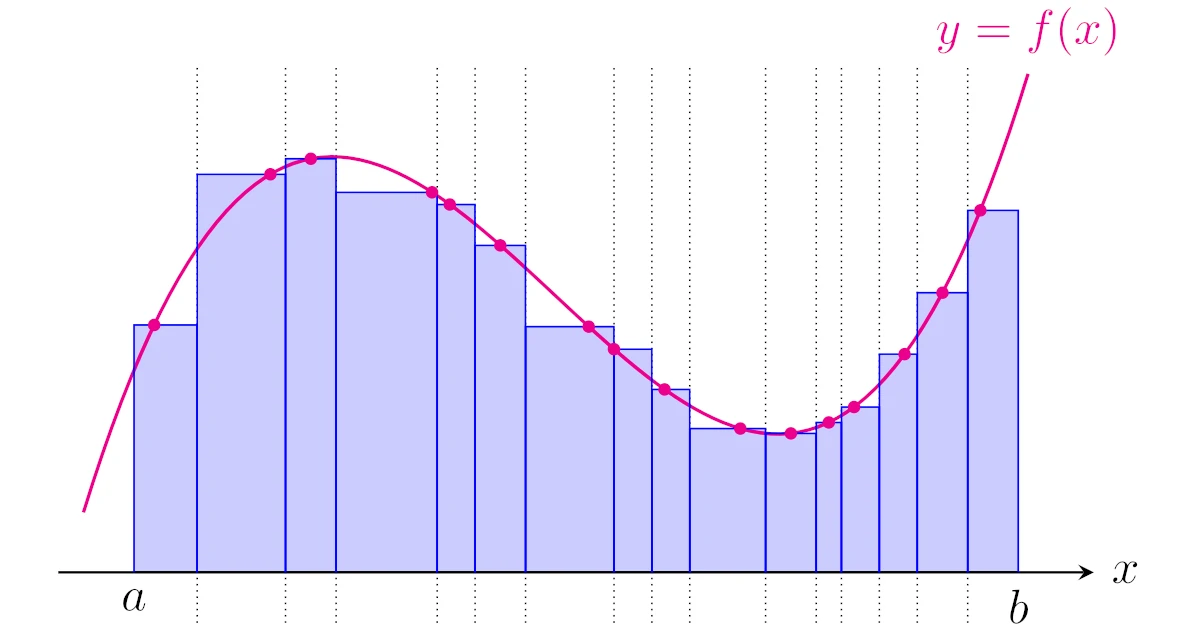
リーマン積分は下図のように，たくさんの短冊に切り分けて長方形で近似する積分でした．

この積分区間$[a,b]$上の変数$x$を考えたとき，$[a,x]$上でのリーマン積分を不定積分といいます．

区間$I\subset\R$上の実数値関数$f$は$I$上リーマン可積分であるとする．また，$a\in I$を任意にとる．このとき，

$\begin{align*}F(x)=\int_{a}^{x}f(t)\,dt\end{align*}$

で定まる関数$F:I\to\R$を$f$の（$a$から$x$までの）不定積分（indefinite integral）という．

$a\in I$のとり方によって不定積分$F$は異なります．しかし，

$a\in I$に対する$f$の不定積分を$F_{a}$
$b\in I$に対する$f$の不定積分を$F_{b}$

とすると，定義から

$\begin{align*}F_{a}(x)-F_{b}(x) =&\int_{a}^{x}f(t)\,dt-\int_{b}^{x}f(t)\,dt \\=&\int_{a}^{b}f(t)\,dt\end{align*}$

なので，$F_{a}(x)$と$F_{b}(x)$の差は定数$\dint_{a}^{b}f(t)\,dt$なので$x$によりません．

つまり，$a\in I$の取り方を変えても，不定積分$F$は定数分しか変わらないわけですね．

原始関数

区間$I\subset\R$上の実数値関数$f$に対して，$I$上微分可能な実数値関数$F$が$F’=f$をみたすとき，$F$を$I$上の$f$の原始関数という．

$F$を微分すれば$f$になるとき，$F$を$f$の原始関数というわけですね．

定数関数の導関数は恒等的に$0$な関数なので，$F$が$f$の原始関数であれば

$\begin{align*}(F+C)'=f+0=f\end{align*}$

となるので，$F+C$も$f$の原始関数ですね．

つまり，$f$の原始関数は定数を加えても$f$の原始関数というわけですね．

微分積分学の基本定理

それでは微分積分学の基本定理の説明に移ります．

微分積分学の基本定理

不定積分と原始関数の定義において

不定積分の定義には微分を用いない
原始関数の定義には積分を用いない

というところが重要です．そのため，不定積分と原始関数の関係を述べることができれば，別々に定義されたはずの積分と微分に関係があることになりますね．

この関係を述べた定理が微分積分学の基本定理で，次の通りです．

［微分積分学の基本定理］$f$を区間$I=[a,b]\subset\R$上の実数値連続関数とする．このとき，次が成り立つ．

$f$の不定積分は，$f$の原始関数である．
$f$の原始関数$G$は，$f$の不定積分$F$と定数$C\in\R$を用いて$G(x)=F(x)+C$（$x\in I$）と表せる．
$f$の原始関数$G$に対して，$\dint_{a}^{b}f(t)\,dt=G(b)-G(a)$が成り立つ．

微分積分学の基本定理は「微積分の基本定理」「微分積分の基本定理」などと呼ぶことも多いです．

微分積分学の基本定理は連続関数に対して成り立つ定理です．高校数学で扱う関数はほとんどが連続関数であるため，高校数学では最初から積分を微分の逆演算として定義しているわけですね．

さて，この微分積分学の基本定理の３つのうち，

(1)では不定積分は原始関数であること
(2)では原始関数は不定積分の定数差のものだけであること

を保証しています．(3)は(1)と(2)を用いて証明でき，この(3)が積分の計算において重要です．

つまり，和の極限で定義されている不定積分がリーマン和を用いずとも，原始関数が分かれば計算できるということを主張しているのが３なわけですね．

証明

それでは微分積分学の基本定理を証明しましょう．

(1) 不定積分が原始関数であることの証明

$I$上の不定積分$F$を$F(x)=\int_{c}^{x}f(t)\,dt$とする（$c\in I$）．

$f$は$I$上で連続だから，任意の$x\in I$と$\epsilon>0$に対して，ある$\delta>0$が存在して，$|t-x|<\delta$なら$|f(t)-f(x)|<\epsilon$を満たす．

よって，$x+h\in I$なる任意の$h\in(-\delta,\delta)\setminus\{0\}$に対して

$\begin{align*}&\abs{\frac{F(x+h)-F(x)}{h}-f(x)} \\=&\frac{1}{|h|}\abs{\bra{\int_{c}^{x+h}f(t)\,dt-\int_{c}^{x}f(t)\,dt}-hf(x)} \\=&\frac{1}{|h|}\abs{\int_{x}^{x+h}f(t)\,dt-\int_{x}^{x+h}f(x)\,dt} \\=&\frac{1}{|h|}\abs{\int_{x}^{x+h}(f(t)-f(x))\,dt} \\\le&\frac{1}{|h|}\abs{\int_{x}^{x+h}|f(t)-f(x)|\,dt}\end{align*}$

となる．$h>0$のとき

$\begin{align*}\frac{1}{|h|}\abs{\int_{x}^{x+h}|f(t)-f(x)|\,dt} <&\frac{1}{h}\int_{x}^{x+h}\epsilon\,dt \\=&\frac{1}{h}\cdot h\epsilon =\epsilon\end{align*}$

$h<0$のとき

$\begin{align*}\frac{1}{|h|}\abs{\int_{x}^{x+h}|f(t)-f(x)|\,dt} =&\frac{1}{-h}\int_{x+h}^{x}|f(t)-f(x)|\,dt \\<&\frac{1}{-h}\int_{x+h}^{x}\epsilon\,dt \\=&\frac{1}{-h}\cdot (-h)\epsilon =\epsilon\end{align*}$

が成り立つから，$\lim\limits_{h\to0}\frac{F(x+h)-F(x)}{h}=f(x)$が得られた．

すなわち，$I$上で$F$は微分可能で$F’=f$となるから，$F$は$I$上の$f$の原始関数である．

(2) 原始関数が不定積分の定数差で表せることの証明

$G$は$f$の原始関数だから定義より$G’=f$であり，$F$は$f$の不定積分だから(1)より$F’=f$である．よって，

$\begin{align*}F'=G'\iff (F-G)'=0\end{align*}$

となるから$F-G$は定数なので，$G$は不定積分の定数差のものに限る．

(3) 積分が原始関数で表せることの証明

(2)の記号を用いる．$F(x)=\dint_{a}^{x}f(t)\,dt$により不定積分$F$を定める．

(2)より$F-G$は定数関数だったから

$\begin{align*}F(x)-G(x)=F(a)-G(a)=-G(a)\end{align*}$

である．ただし，最後の等式では$F(a)=\int_{a}^{a}f(t)\,dt=0$であることを用いた．よって

$\begin{align*}\int_{a}^{b}f(t)\,dt=F(b)=G(b)-G(a)\end{align*}$

が成り立つ．

証明に関する補足

(1)の証明について，いくつか簡単な補足をします．

補足１

$f(x)$は$t$に無関係なので，$t$で積分すると

$\begin{align*}hf(x)=\int_{x}^{x+h}f(x)\,dt\end{align*}$

となります．

$t$の積分において$x$は定数として扱ってもよいのでした．

補足２

リーマン積分$\dint_{a}^{b}f(t)\,dt$の定義式は

$\begin{align*}\lim_{\max_{i}\{x_i-x_{i-1}\}\to0}\sum_{i=1}^{n}f(\xi)(x_i-x_{i-1})\end{align*}$

という形でしたが，$x_i-x_{i-1}$の部分を$|x_i-x_{i-1}|$に置き換えたものを

$\begin{align*}\int_{a}^{b}f(t)\,|dt| :=\lim_{\max_{i}\{x_i-x_{i-1}\}\to0}\sum_{i=1}^{n}f(\xi)|x_i-x_{i-1}|\end{align*}$

とする記法があります．

この記法のもとでは$a,b\in\R$の大小関係が不明でも，$0\le f(t)\le g(t)$なら

$\begin{align*}\int_{a}^{b}f(t)\,|dt| \le\int_{a}^{b}g(t)\,|dt|\end{align*}$

が成り立ちます．このことを用いると$|f(t)-f(x)|<\epsilon$から

$\begin{align*}&\abs{\frac{F(x+h)-F(x)}{h}-f(x)} \\\le&\frac{1}{|h|}\int_{x}^{x+h}|f(t)-f(x)|\,|dt| \\\le&\frac{1}{|h|}\int_{x}^{x+h}\epsilon\,|dt| =\frac{1}{|h|}|h|\epsilon =\epsilon\end{align*}$