正の整数
ですね.実はガンマ関数という関数があり,このガンマ関数は階乗の実数(複素数)への拡張としてよく知られています.
ガンマはギリシャ文字の
ガンマ関数は微分積分学だけでなく,統計学や複素解析においても現れる重要な関数です.
この記事では
- ガンマ関数の定義と具体例
- ガンマ関数の基本性質
- ガンマ関数とベータ関数との関係
を順に説明します.
ガンマ関数の定義と具体例
まずはガンマ関数
ガンマ関数の定義
正の実数
で定まる実数値関数
広義積分
ガンマ関数は実部が正の複素数に対しても同様に定義できますが,この記事では主に実数の場合を説明します.
具体的に
具体例1(
となりますね.
のちに説明するように,0以上の整数
具体例2(
となりますね.
が成り立ちます.最後の積分はガウス積分で
このように
ガンマ関数の性質
ガンマ関数の基本性質を解説します.
ガンマ関数の別の表し方
ガンマ関数は以下のように表すこともできます.
正の実数
が成り立つ.
これは先ほど求めた
ガンマ関数の定義
であり,
が成り立つ.
冒頭でも説明したように,ガンマ関数は階乗の一般化と捉えることができます.このことを示すために重要な性質を証明しましょう.
正の実数
が成り立つ.
ガンマ関数の定義と部分積分により
が成り立つ.
この命題を用いて,具体的に
具体例3(
となって,具体例1で計算した
このように,
具体例4(
となって,具体例2で計算した
ガンマ関数と階乗の関係
具体例3の
正の整数
が成り立つ.
数学的帰納法により示す.
[1]
[2]ある
が成り立つ.
ベータ関数との関係
ガンマ関数と関係の深い関数にベータ関数があります.ベータ関数の定義は次の通りです.
正の実数
で定まる2変数関数
とも表せますね.
さて,ガンマ関数を用いると,ベータ関数は以下のように表せます.
正の実数
が成り立つ.
である.極座標変換
となる.上で示したガンマ関数の別の表し方から
となる.以上より
補足
最後にいくつか補足します.
複素関数としてのガンマ関数
ガンマ関数は複素変数に対しても定義されます.
実部が正の複素数
で定まる複素関数
ただし,
実数の場合と同様に次が成り立ちます.
実部が正の実数
が成り立つ.
複素関数論においてガンマ関数は非常に興味深い正則関数ですが,この記事では以上の説明に留めます.
広義積分としてのガンマ関数
ガンマ関数
- 0付近での積分
- 無限遠方までの積分
のふたつの意味で広義積分となっており,このことをきちんと表すと
ということになりますね.
一方,
ということになりますね.
ガンマ関数が収束することの証明
そもそも「ガンマ関数
と定める」というためには,正の実数
直観的には,
- 無限遠方では(
- 0付近では
ということになりますね.
正の実数
極限
が成り立つ.以下,
これらが示されれば,広義積分
被積分関数
なので,
なので,
- 一つ目の等号では
- 二つ目の等号では
に注意.
一方,
と発散し,
と発散しますね.

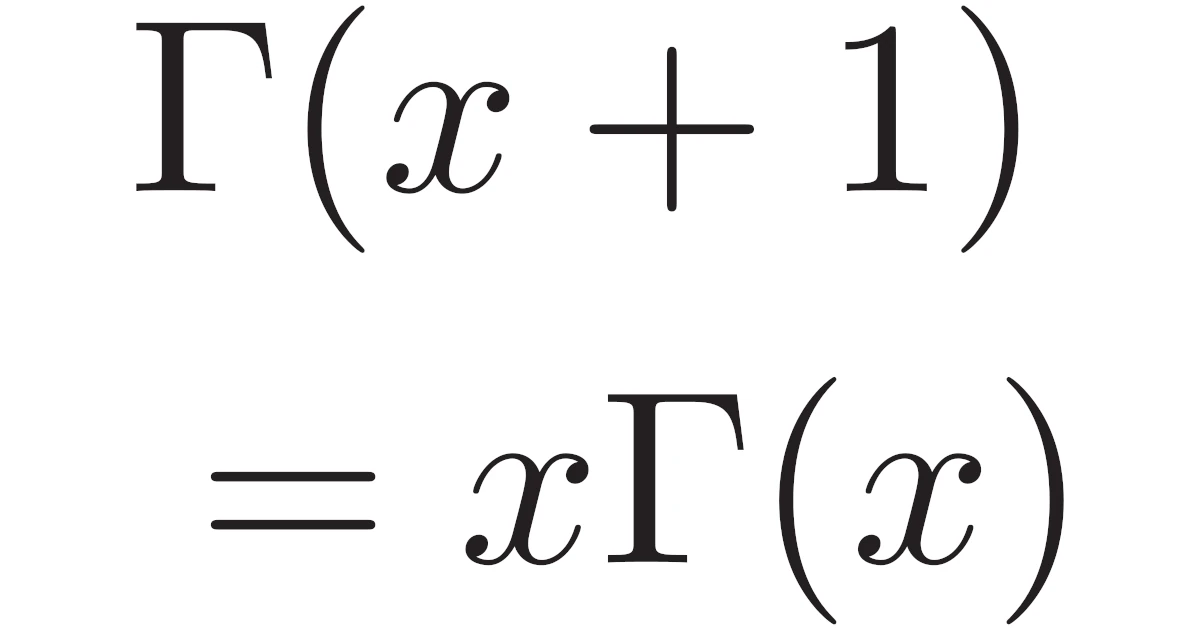
コメント