フレネル積分を複素積分で計算する｜cos(x²), sin(x²)の広義積分

２つの広義積分

$\begin{align*}\int_{0}^{\infty}\cos{(x^2)}\,dx,\quad \int_{0}^{\infty}\sin{(x^2)}\,dx\end{align*}$

はフレネル積分と呼ばれており，どちらも$\dfrac{\sqrt{\pi}}{2\sqrt{2}}$に収束することを複素積分を用いて示すことができます．

この複素積分の計算では積分経路のとり方がポイントになっており，このことに気付くとフレネル積分を一般化した

$\begin{align*}&\int_{0}^{\infty}\cos{(x^n)}\,dx=\Gamma\bra{1+\frac{1}{n}}\cos{\bra{\frac{\pi}{2n}}},\quad \\&\int_{0}^{\infty}\sin{(x^n)}\,dx=\Gamma\bra{1+\frac{1}{n}}\sin{\bra{\frac{\pi}{2n}}}\end{align*}$

も複素積分を用いて示すことができます（$n=2,3,4,\dots$）．

この記事では

フレネル積分の複素積分による計算
フレネル積分の一般化
補足（ルベーグ積分では積分不可能）

を順に解説します．

他に複素積分を用いて求められる有名な広義積分としては，ディリクレ積分$\dint_{0}^{\infty}\dfrac{\sin{x}}{x}\,dx=\frac{\pi}{2}$などがあります．

フレネル積分の複素積分による計算
1. 広義積分を求めるための複素積分の簡単な例
2. フレネル積分の計算
フレネル積分の一般化
補足（ルベーグ積分の場合）

フレネル積分の複素積分による計算

冒頭で述べたように，次のフレネル積分の値を求めることがこの記事のメインです．

広義積分について，

$\begin{align*}\int_{0}^{\infty}\cos{(x^2)}\,dx=\int_{0}^{\infty}\sin{(x^2)}\,dx=\frac{\sqrt{\pi}}{2\sqrt{2}}\end{align*}$

が成り立つ．この積分をフレネル積分（Fresnel integrals）という．

広義積分を求めるための複素積分の簡単な例

広義積分を計算したいとき，複素積分を用いるとうまくいくことがよくあります．例えば，

$\begin{align*}I:=\int_{-\infty}^{\infty}\frac{\cos{x}}{1+x^2}\,dx\end{align*}$

を計算したいときは，$R>1$に対して$\C$上の経路

$\begin{align*}&C_1:=\set{z=x\in\C}{x\in[-R,R]}, \\&C_2:=\set{z=Re^{i\theta}\in\C}{\theta\in[0,\pi]}\end{align*}$

を定めると，

$\begin{align*}I&=\lim_{R\to\infty}\operatorname{Im}\int_{-R}^{R}\frac{e^{ix}}{1+x^2}\,dx =\lim_{R\to\infty}\operatorname{Im}\int_{C_1}\frac{e^{iz}}{1+z^2}\,dz \\&=\lim_{R\to\infty}\operatorname{Im}\bra{\int_{C_1\cup C_2}\frac{e^{iz}}{1+z^2}\,dz-\int_{C_2}\frac{e^{iz}}{1+z^2}\,dz}\end{align*}$

と目的の広義積分を変形でき，留数定理より$\dint_{C_1\cup C_2}\dfrac{e^{iz}}{1+z^2}\,dz$が計算でき，$\lim\limits_{R\to\infty}\dint_{C_2}\dfrac{e^{iz}}{1+z^2}\,dz=0$が証明できて，目的の広義積分が求められます．

留数定理による広義積分の計算｜例題から使い方・考え方を解説

留数定理は複素積分と留数の関係を述べた複素解析の定理で，留数定理を用いれば広義積分の値が簡単に計算できることもよくあります．この記事では留数定理を説明したのち，留数定理の使い方を例題をもとに解説しています．

フレネル積分の計算

いまみたように$\cos$, $\sin$は$\exp$で複素積分を考えたのち実部・虚部をとるとうまくいきます．

フレネル積分の場合も$e^{iz^2}=\cos{(z^2)}+i\sin{(z^2)}$を適切な経路上で積分することでうまく計算することができます．

（再掲）広義積分について，

$\begin{align*}\int_{0}^{\infty}\cos{(x^2)}\,dx=\int_{0}^{\infty}\sin{(x^2)}\,dx=\frac{\sqrt{\pi}}{2\sqrt{2}}\end{align*}$

が成り立つ．この積分をフレネル積分（Fresnel integrals）という．

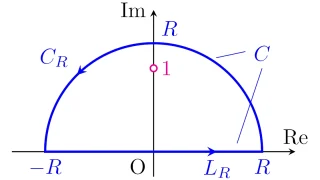
$R>0$に対して$\C$上の経路

$\begin{align*}&C_1:=\set{z=x\in\C}{x\in[0,R]}, \\&C_2:=\set{z=Re^{i\theta}\in\C}{\theta\in\brc{0,\frac{\pi}{4}}} \\&C_3:=\set{z=(R-r)e^{\pi i/4}\in\C}{r\in[0,R]}\end{align*}$

を定める．

$C_1$, $C_3$上の複素積分

複素積分$\dint_{C_1}e^{iz^2}\,dz$, $\dint_{C_3}e^{iz^2}\,dz$を考える．

$z\in C_1$を$z=x$（$x\in[0,R]$）とおくと，$\frac{dz}{dx}=1$なので

$\begin{align*}\int_{C_1}e^{iz^2}\,dz=\int_{0}^{R}e^{ix^2}\,dx=\int_{0}^{R}(\cos{x^2}+i\sin{x^2})\,dx\end{align*}$

が成り立つ．また，$z\in C_3$を$z=(R-r)e^{\pi i/4}$（$r\in[0,R]$）とおくと，$\frac{dz}{dr}=-e^{\pi i/4}$なので

$\begin{align*}\int_{C_3}e^{iz^2}\,dz&=\int_{0}^{R}e^{i(R-r)^2e^{\pi i/2}}(-e^{\pi i/4})\,dr \\&=-e^{\pi i/4}\int_{0}^{R}e^{-(R-r)^2}\,dr=-e^{\pi i/4}\int_{0}^{R}e^{-x^2}\,dx\end{align*}$

が成り立つ．ただし，最後の等号では$x=R-r$とおいた．

$C_2$上の複素積分の極限

複素積分の極限$\lim\limits_{R\to\infty}\dint_{C_2}e^{iz^2}\,dz=0$を示す．

$z\in C_2$を$z=Re^{i\theta}$（$\theta\in[0,\frac{\pi}{4}]$）とおくと，$\frac{dz}{d\theta}=iRe^{i\theta}$なので

$\begin{align*}&\abs{\int_{C_2}e^{iz^2}\,dz}=\abs{\int_{0}^{\pi/4}e^{iR^2e^{2i\theta}}(iRe^{i\theta})\,d\theta} \\&\le\int_{0}^{\pi/4}\abs{e^{iR^2e^{2i\theta}}(iRe^{i\theta})}\,d\theta=R\int_{0}^{\pi/4}\abs{e^{iR^2e^{2i\theta}}}\,d\theta\end{align*}$

である．ここで，

$\begin{align*}\abs{e^{iR^2e^{2i\theta}}}=\abs{e^{iR^2\cos{2\theta}-R^2\sin{2\theta}}}=e^{-R^2\sin{2\theta}}\end{align*}$

であり，$\theta\in[0,\frac{\pi}{4}]$に対して$\sin{2\theta}\ge\frac{4\theta}{\pi}$である．

よって，

$\begin{align*}&\abs{\int_{C_2}e^{iz^2}\,dz}\le R\int_{0}^{\pi/4}e^{-4R^2\theta/\pi}\,d\theta \\&=R\brc{-\frac{\pi e^{-4R^2\theta/\pi}}{4R^2}}_{0}^{\pi/4}=\frac{\pi(1-e^{-R^2})}{4R} \xrightarrow[]{R\to\infty}0\end{align*}$

が成り立つ．

$C_1\cup C_2\cup C_3$上の複素積分

$C_1\cup C_2\cup C_3$は長さ有限の閉曲線（扇形の周）であり，複素関数$z\mapsto e^{iz^2}$は整関数（$\C$上の正則関数）なので，コーシーの積分定理より

$\begin{align*}\int_{C_1\cup C_2\cup C_3}e^{iz^2}\,dz=0\end{align*}$

である．よって，両辺で極限をとって

$\begin{align*}&\int_{0}^{\infty}(\cos{x^2}+i\sin{x^2})\,dx-e^{\pi i/4}\int_{0}^{\infty}e^{-x^2}\,dx=0 \\&\iff \int_{0}^{\infty}(\cos{x^2}+i\sin{x^2})\,dx=\bra{\frac{1}{\sqrt{2}}+i\frac{1}{\sqrt{2}}}\frac{\sqrt{\pi}}{2}\end{align*}$

が成り立つ．ただし，ガウス積分より

$\begin{align*}\int_{0}^{\infty}e^{-x^2}\,dx=\frac{\sqrt{\pi}}{2}\end{align*}$

であることを用いた．よって，実部と虚部を比較して

$\begin{align*}\int_{0}^{\infty}\cos{(x^2)}\,dx=\int_{0}^{\infty}\sin{(x^2)}\,dx=\frac{\sqrt{\pi}}{2\sqrt{2}}\end{align*}$

を得る．

フレネル積分の一般化

上のフレネル積分の計算のポイントは経路$C_3$です．

$z\in C_3$の偏角が$\frac{\pi}{4}$であることから，積分経路$C_3$上の複素積分では被積分関数が実数値関数になります：

$\begin{align*}e^{iz^2}=e^{i(R-r)^2e^{\pi i/2}}=\exp\bra{-(R-r)^2}\end{align*}$

よって，２以上の整数$n$に対して

$\begin{align*}\int_{0}^{\infty}\cos{(x^n)}\,dx,\quad \int_{0}^{\infty}\sin{(x^n)}\,dx\end{align*}$

も偏角が$\frac{\pi}{2n}$の経路をとれば，同様に計算ができそうですね．

２以上の整数$n$に対して，次の等式を示せ．

$\begin{align*}&\int_{0}^{\infty}\cos{(x^n)}\,dx=\Gamma\bra{1+\frac{1}{n}}\cos{\bra{\frac{\pi}{2n}}}, \\&\int_{0}^{\infty}\sin{(x^n)}\,dx=\Gamma\bra{1+\frac{1}{n}}\sin{\bra{\frac{\pi}{2n}}}\end{align*}$

ただし，積分は広義積分で，$\Gamma$はガンマ関数である：

$\begin{align*}\Gamma(\alpha)=\int_{0}^{\infty}t^{\alpha-1}e^{-t}\,dt\quad(\operatorname{Re}\alpha>0).\end{align*}$

$R>0$に対して$\C$上の経路

$\begin{align*}&C_1:=\set{z=x\in\C}{x\in[0,R]}, \\&C_2:=\set{z=Re^{i\theta}\in\C}{\theta\in\brc{0,\frac{\pi}{2n}}} \\&C_3:=\set{z=(R-r)e^{\pi i/2n}\in\C}{r\in[0,R]}\end{align*}$

を定める．

$C_1$, $C_2$, $C_3$上の複素積分

経路$C_1$, $C_3$上の複素積分について，

$\begin{align*}\int_{C_1}e^{iz^n}\,dz&=\int_{0}^{R}e^{ix^n}\,dx \\&=\int_{0}^{\infty}(\cos{x^n}+i\sin{x^n})\,dx, \\\int_{C_3}e^{iz^n}\,dz&=\int_{0}^{R}e^{i(R-r)^ne^{\pi i/2}}(-e^{\pi i/2n})\,dr \\&=-e^{\pi i/2n}\int_{0}^{R}e^{-x^n}\,dx\end{align*}$

が成り立つ．また，経路$C_2$上の複素積分について，

$\begin{align*}&\abs{\int_{C_2}e^{iz^n}\,dz}=\abs{\int_{0}^{\pi/2n}e^{iR^ne^{ni\theta}}(iRe^{i\theta})\,d\theta} \\&\le R\int_{0}^{\pi/2n}e^{-R^n\sin{n\theta}}\,d\theta\le R\int_{0}^{\pi/2n}e^{-2nR^n\theta/\pi}\,d\theta \\&=R\brc{-\frac{\pi e^{-2nR^n\theta/\pi}}{2nR^n}}_{0}^{\pi/2n}=\frac{\pi(1-e^{-R^n})}{2nR^{n-1}}\xrightarrow[]{R\to\infty}0\end{align*}$

が成り立つ．

$C_1\cup C_2\cup C_3$上の複素積分

$C_1\cup C_2\cup C_3$は長さ有限の閉曲線（扇形の周）であり，複素関数$z\mapsto e^{iz^n}$は整関数（$\C$上の正則関数）なので，コーシーの積分定理より

$\begin{align*}\int_{C_1\cup C_2\cup C_3}e^{iz^2}\,dz=0\end{align*}$

である．よって，両辺で極限をとって実部と虚部を比較し

$\begin{align*}&\int_{0}^{\infty}\cos{x^n}\,dx=\cos{\bra{\frac{\pi}{2n}}}\int_{0}^{\infty}e^{-x^n}\,dx, \\&\int_{0}^{\infty}\sin{x^n}\,dx=\sin{\bra{\frac{\pi}{2n}}}\int_{0}^{\infty}e^{-x^n}\,dx\end{align*}$

が成り立つ．

$e^{-x^n}$の広義積分をガンマ関数で表す

ここで$t=x^n$とおくと$\frac{dt}{dx}=nx^{n-1}=nt^{1-\frac{1}{n}}$なので，

$\begin{align*}\int_{0}^{\infty}e^{-x^n}\,dx=\frac{1}{n}\int_{0}^{\infty}t^{\frac{1}{n}-1}e^{-t}\,dt=\frac{1}{n}\Gamma\bra{\frac{1}{n}}=\Gamma\bra{1+\frac{1}{n}}\end{align*}$

である．ただし，最後の等号ではガンマ関数の性質$\Gamma(\alpha+1)=\alpha\Gamma(\alpha)$を用いた．

以上より，

$\begin{align*}&\int_{0}^{\infty}\cos{x^n}\,dx=\Gamma\bra{1+\frac{1}{n}}\cos{\bra{\frac{\pi}{2n}}} \\&\int_{0}^{\infty}\sin{x^n}\,dx=\Gamma\bra{1+\frac{1}{n}}\sin{\bra{\frac{\pi}{2n}}}\end{align*}$

を得る．

$\sin{x}$, $\cos{x}$が恒等的に０ではない周期関数なので，$n=1$のときは発散しますね．

補足（ルベーグ積分の場合）

フレネル積分が収束するのは，広義積分が

$\begin{align*}&\int_{0}^{\infty}\cos{(x^2)}\,dx=\lim_{R\to\infty}\int_{0}^{R}\cos{(x^2)}\,dx \\&\int_{0}^{\infty}\sin{(x^2)}\,dx=\lim_{R\to\infty}\int_{0}^{R}\sin{(x^2)}\,dx\end{align*}$

と定義されているためです．

つまり，０から$R$まで積分するとそこまでのプラスとマイナスが打ち消し合い，そののちに極限$R\to\infty$をとるため交項級数のように収束しているわけですね．

一方，フレネル積分をルベーグ積分として考えることはできません．これはルベーグ可測関数$f$のルベーグ積分が

正成分のルベーグ積分$\dint_{A}f_+(x)\,dx$（$f_{+}:=\max\{0,f\}$）
負成分のルベーグ積分$\dint_{A}f_-(x)\,dx$（$f_{-}:=-\min\{0,f\}$）

を別々に定義して，いずれか一方が有限の時に

$\begin{align*}\int_{A}f(x)\,dx=\int_{A}f_+(x)\,dx-\int_{A}f_-(x)\,dx\end{align*}$

と定義されるためです．

関数$\cos{(x^2)}$, $\sin{(x^2)}$の正成分のルベーグ積分も，負成分のルベーグ積分も$\infty$となってしまうため，フレネル積分はルベーグ積分では定義されないわけですね．

一般に有界閉区間上のリーマン積分はルベーグ積分可能でしたが，このフレネル積分のように，広義リーマン積分可能であっても必ずしもルベーグ積分が定義されるとは限りません．

他にディリクレ積分

$\begin{align*}\int_{0}^{\infty}\frac{\sin{x}}{x}\,dx=\frac{\pi}{2}\end{align*}$

も広義積分では定義できますが，ルベーグ積分では定義されない積分として有名です．

フレネル積分を複素積分で計算する｜cos(x²)，sin(x²)の広義積分

フレネル積分の複素積分による計算

広義積分を求めるための複素積分の簡単な例

フレネル積分の計算

$C_1$, $C_3$上の複素積分

$C_2$上の複素積分の極限

$C_1\cup C_2\cup C_3$上の複素積分

フレネル積分の一般化

$C_1$, $C_2$, $C_3$上の複素積分

$C_1\cup C_2\cup C_3$上の複素積分

$e^{-x^n}$の広義積分をガンマ関数で表す

補足（ルベーグ積分の場合）

コメント