ルベーグ積分において,例えば$\R$上の可積分関数$f,g$が零集合(測度0の集合)上のみで異なるとき,
\begin{align*}\int_{\R}f(x)\,dx=\int_{\R}g(x)\,dx\end{align*}
が成り立ちます.
一般の測度空間でも零集合上のことは無視しても結果に影響がないことはよくあり,零集合上でのみ例外であることを「ほとんど至る所で」と表現します.
この記事では
- 「ほとんど至る所で」の定義
- 「ほとんど至る所で」の具体例
- 「ほとんど至る所で」の応用
を順に説明します.
「ほとんど至る所で」の定義
測度空間上の零集合上のみで条件を満たさないことを次のように言います.
$(X,\mathcal{F},\mu)$を測度空間とし,集合$A\in\mathcal{F}$と,$x\in A$に関する条件$P(x)$を考える.
条件$P(x)$が成り立たない$x\in A$全部の集合が零集合であるとき,$A$上ほとんど至る所で(almost everywhere)条件$P$が成り立つといい,$P(x)\ \text{a.e.}\ x\in A$などと表す.
$A$が明らかな場合は$P(x)\ \text{a.e.}\ x$と表したり,よりシンプルに$P\ \text{a.e.}$と表すこともよくあります.
一般の測度空間$(X,\mathcal{F},\mu)$においては「ほとんど至る所で」と言いますが,確率空間においては次のように言います.
$(\Omega,\mathcal{F},\mathbb{P})$を確率空間とし,$\omega\in\Omega$に関する条件$A(\omega)$を考える.
条件$A(\omega)$が成り立たない$\omega\in\Omega$全部の集合の確率が0であるとき,ほとんど確実に(almost surely)条件$A$が成り立つといい,$A(\omega)\ \text{a.s.}\ \omega$などと表す.
こちらは「起こり得るかもしれないが,確率としては0であるような条件$A(\omega)$」のことをいうわけですね.
「ほとんど至る所で」の具体例
以下では測度空間として$\R$上のルベーグ測度空間を考え,$m$をルベーグ測度とします.
具体例1(本質的に恒等的に値0をとる関数)
恒等的に値0をとる$\R$上の関数を$\m{0}_{\R}$で表し,$\R$上の関数$f$を
\begin{align*}f(x)=\begin{cases}0&(x\neq0)\\1&(x=0)\end{cases}\end{align*}
で定めます.
$f(x)=\m{0}_{\R}(x)$が成り立たないのは$x=0$のときに限るので,
\begin{align*}m(\set{x\in\R}{f(x)\neq 0_{\R}(x)})=m(\{0\})=0\end{align*}
となります.よって,$\R$上ほとんど至る所で$f(x)\neq 0_{\R}(x)$が成り立つということができ,これを
\begin{align*}f(x)=\m{0}_{\R}(x)\ \text{a.e.}\ x\in\R\end{align*}
などと表すわけですね.
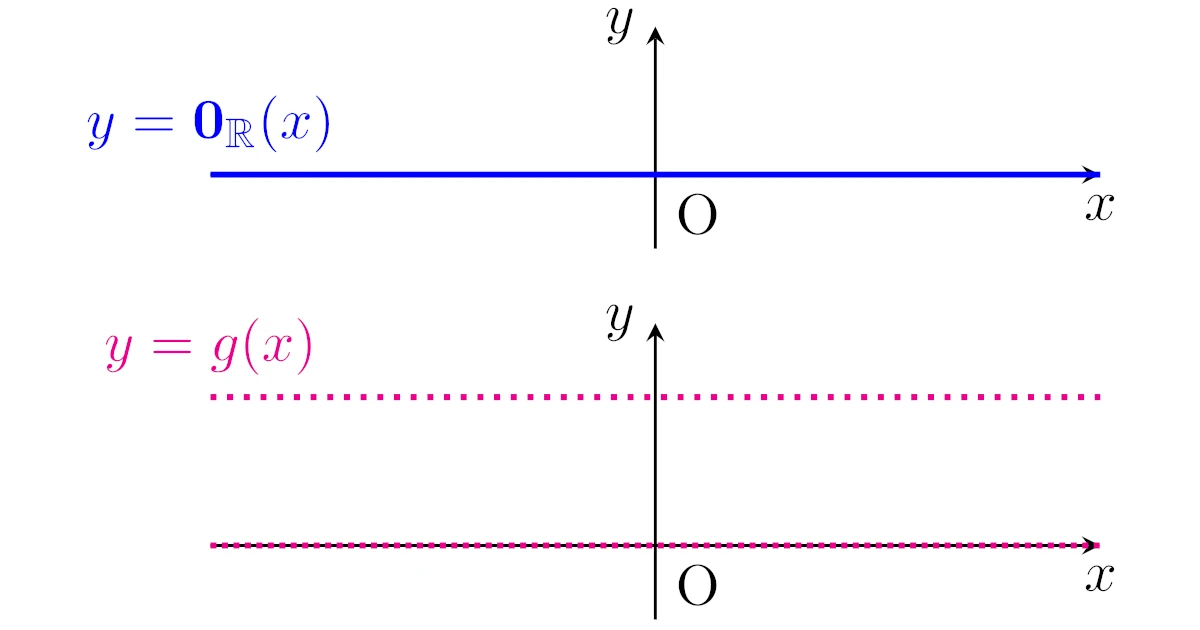
具体例2(ディリクレ関数)
具体例1と同様に恒等的に値0をとる$\R$上の関数を$\m{0}_{\R}$で表します.また,ディリクレ(Dirichlet)関数$g$は
\begin{align*}g(x)=\begin{cases}0&(x\in\R\setminus\Q)\\1&(x\in\Q)\end{cases}\end{align*}
で定まる$\R$上の関数のことをいいます.
有理数全部の集合$\Q$が零集合であることに注意すると,
\begin{align*}m(\set{x\in\R}{g(x)\neq\m{0}_{\R}(x)})=m(\Q)=0\end{align*}
となります.よって,$\R$上ほとんど至る所で$g(x)=0_{\R}(x)$が成り立つということができ,これを
\begin{align*}g(x)=\m{0}_{\R}(x)\ \text{a.e.}\ x\in\R\end{align*}
などと表すわけですね.
一般に可算集合が零集合だったので,可算集合上のみで異なる2つの関数は本質的に等しいと考えられますね.
具体例3(ほとんど至る所で各点収束)
$I:=[0,1]$とし,$I$上の関数列$\{h_n\}$を$h_n(x)=\dfrac{1}{1+x^n}$で定めると,
\begin{align*}\lim_{n\to\infty}h_n(x)=h(x):=\begin{cases}1&(0\le x<1)\\\dfrac{1}{2}&(x=1)\end{cases}\end{align*}
と各点収束します.
また,恒等的に値1をとる$I$上の関数を$\mathbb{I}_{I}$で表しましょう.
このとき,
\begin{align*}m(\set{x\in\R}{h(x)\neq \mathbb{I}_{I}(x)})=m(\{1\})=0\end{align*}
となります.よって,$I$上ほとんど至る所で$\{h_n\}$は$\mathbb{I}_{I}$に収束するということができ,これを
\begin{align*}\lim_{n\to\infty}h_n(x)=\mathbb{I}_{I}(x)\ \text{a.e.}\ x\in\R\end{align*}
などと表すわけですね.
「ほとんど至る所で」の応用例
「ほとんど至る所」の応用例を考えましょう.
ルベーグ可積分関数はほとんど至る所で有限
普通,ルベーグ可測関数の終集合は拡大実数$\overline{\R}=\R\cup\{\pm\infty\}$として考えることを思い出しておきましょう.
$X’:=\set{x\in X}{|f(x)|=\infty}$とする.$f$は$X$上のルベーグ可測関数だから,$X’$はルベーグ可測集合である.よって,
\begin{align*}\infty>\int_{X}|f(x)|\,dx\ge\int_{X’}|f(x)|\,dx=\infty\cdot m(X’)\end{align*}
が成り立つ.もし$m(X’)>0$なら$\infty\cdot m(X’)=\infty$となって,矛盾するから$m(X’)=0$が成り立つ.
$X’$の定義から,$X$上ほとんど至る所で$|f(x)|<\infty$となる.
ほとんど至る所で等しい2つの関数の積分
ルベーグ可測集合$X\subset\R^d$上のルベーグ可測関数$f$, $g$を考える.$f$が$X$上のルベーグ可積分関数で,$X$上ほとんど至る所で$f=g$なら,$g$も$X$上のルベーグ可積分関数で
\begin{align*}\int_{X}f(x)\,dx=\int_{X}g(x)\,dx\end{align*}
が成り立つ.
$X’:=\set{x\in X}{f(x)=g(x)}$とすると,
\begin{align*}\int_{X’}f(x)\,dx=\int_{X’}g(x)\,dx\end{align*}
が成り立つ.また,$X$上ほとんど至る所で$f=g$だから$m(X\setminus X’)=0$なので,
\begin{align*}\int_{X\setminus X’}f(x)\,dx=0,\quad
\int_{X\setminus X’}g(x)\,dx=0\end{align*}
である.よって,
\begin{align*}\int_{X}f(x)\,dx
&=\int_{X’}f(x)\,dx+\int_{X\setminus X’}f(x)\,dx
\\&=\int_{X’}g(x)\,dx+\int_{X\setminus X’}g(x)\,dx
=\int_{X}g(x)\,dx\end{align*}
を得る.
同値関係による同一視
ほとんど至る所で等しい2つのルベーグ可測関数を関係付けると同値関係となります.
$m$を$\R^d$上のルベーグ測度とする.ルベーグ可測集合$X\subset\R^d$上のルベーグ可測集合全部の族に,関係$\sim$を
\begin{align*}f\sim g\stackrel{\mathrm{def.}}{\iff}m(\set{x\in X}{f(x)\neq g(x)})=0\end{align*}
を定めると,関係$\sim$は同値関係となる.
つまり,ほとんどいたるところ等しい関数たちをまとめてグループ分けできるということですね.
[反射律]任意のルベーグ可測関数$f$に対して,
\begin{align*}m(\set{x\in X}{f(x)\neq f(x)})=m(\emptyset)=0\end{align*}
が成り立つから$f\sim f$である.
[対称律]ルベーグ可測関数$f,g$が$f\sim g$を満たすとき,
\begin{align*}m(\set{x\in X}{g(x)\neq f(x)})=m(\set{x\in X}{f(x)\neq g(x)})=0\end{align*}
が成り立つから$g\sim f$である.
[推移律]ルベーグ可測関数$f,g,h$が$f\sim g$かつ$g\sim h$を満たすとき,
\begin{align*}&\set{x\in X}{f(x)=g(x)}\cap\set{x\in X}{g(x)=h(x)}
\\&\subset\set{x\in X}{f(x)=h(x)}\end{align*}
なので,$X$上で補集合を考えて
\begin{align*}&\set{x\in X}{f(x)\neq g(x)}\cup\set{x\in X}{g(x)\neq h(x)}
\\&\supset\set{x\in X}{f(x)\neq h(x)}\end{align*}
\begin{align*}&m(\set{x\in X}{f(x)\neq h(x)})
\\&\le m(\set{x\in X}{f(x)\neq g(x)})+m(\set{x\in X}{g(x)\neq h(x)})
\\&=0+0=0\end{align*}
が成り立つから$f\sim h$である.
$p\ge1$に対して「$p$乗ルベーグ可積分関数全部の集合でほとんど至る所で等しい関数たちを同一視してできる空間」は適切なノルムによりバナッハ空間(完備ノルム空間)になります.
この空間をルベーグ空間と呼び,$L^p$と表します.
ルベーグ空間$L^p$は解析学における基本的な関数空間のひとつとなっています.

コメント