ルベーグ可測関数の定義と具体例｜必要十分条件も２つ紹介

ルベーグ積分はどんな関数に対しても定義できるわけではなく，ルベーグ可測関数と呼ばれる関数に限って定義されます．

そのため，ルベーグ積分を考える上でルベーグ可測関数がどのような関数であるかを知っておくことは大切です．

この記事では

ルベーグ可測関数の定義
ルベーグ可測関数の具体例
ルベーグ可測関数であるための必要十分条件

を順に説明します．

以下ではルベーグ可測集合のことを単に「可測集合」と呼び，$\R$上のルベーグ可測集合族を$\mathcal{L}$で表します．

「ルベーグ積分の基本」の一連の記事

ルベーグ積分入門
1. 0 ルベーグ積分の基礎｜リーマン積分の先へ！積分の歴史から紹介

ルベーグ測度

ルベーグ可測関数とルベーグ積分

ルベーグ積分の性質と項別積分

ルベーグ積分の参考文献
1. ルベグ積分入門
2. ルベーグ積分と関数解析
ルベーグ可測関数の定義
ルベーグ可測関数の具体例
ルベーグ可測関数であるための必要十分条件
1. 必要十分条件１
2. 必要十分条件２

ルベーグ積分の参考文献

以下はルベーグ積分に関するオススメの教科書です．

ルベグ積分入門

ロングセラーの入門書です．専門書ですが，文庫なので安く購入できるのも魅力です．

ルベーグ積分と関数解析

ルベーグ積分から更なるステップに進みたい人向けの教科書です．

ルベーグ可測関数の定義

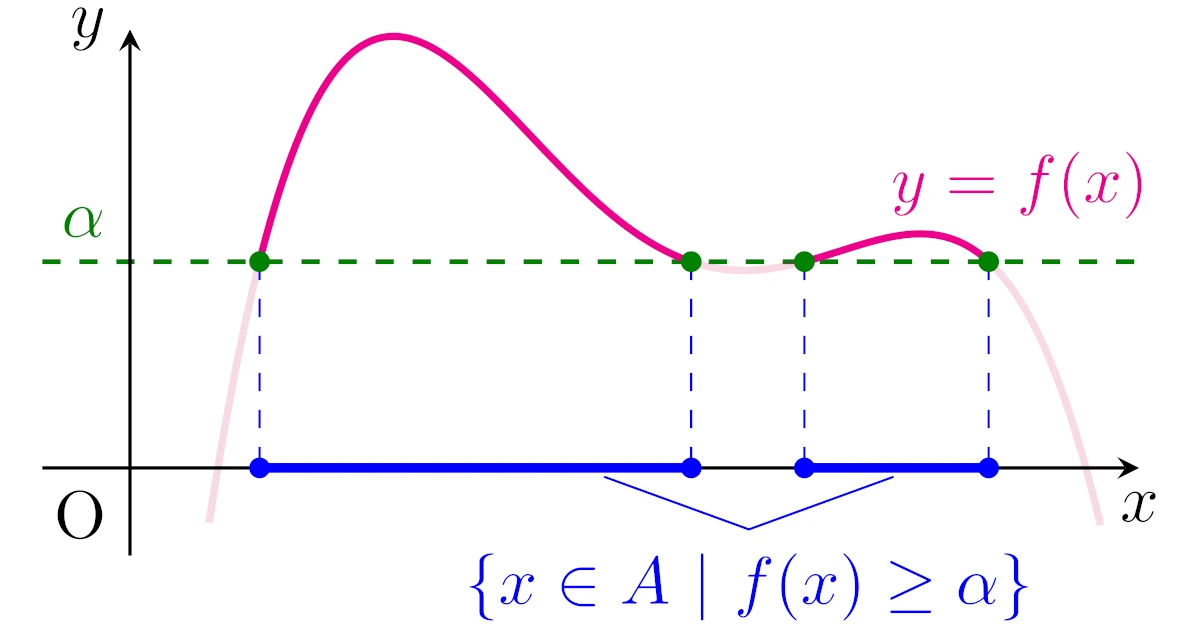
任意の$\alpha\in\R$に対しても，関数$f$が$\alpha$以上となる$x$の集合が可測集合であるとき$f$を可測関数といいます．

可測集合$A$に対して，関数$f:A\to\overline{\R}$が$A$上ルベーグ可測関数または単に可測関数であるとは，任意の$\alpha\in\R$に対して

$\begin{align*}\set{x\in A}{f(x)\ge\alpha}\end{align*}$

が可測集合であることをいう．

ただし，$f$の終集合$\overline{\R}$は拡大実数$\R\cup\{\infty,-\infty\}$である．

ここまでで

ルベーグ可測集合
ルベーグ可測関数

の２つの「可測」が定義されました．そのため，「可測」とあったときには可測集合なのか可測関数なのか意識するようにしてください．

ルベーグ可測関数の具体例

いくつか具体的に可測関数を考えてみましょう．以下では

$\R$と$\emptyset$は可測集合
一般に区間は可測集合

であることに注意しておきましょう．

例１（１次関数）

関数$f:\R\to\R$を$f(x)=\frac{1}{2}x$で定めるとき，$f$が$\R$上ルベーグ可測関数であることを証明せよ．

任意に$\alpha\in\R$に対して，

$\begin{align*}\set{x\in\R}{f(x)\ge\alpha} &=\set{x\in\R}{\frac{1}{2}x\ge\alpha} \\&=\set{x\in\R}{x\ge2\alpha} \\&=[2\alpha,\infty)\in\mathcal{L}\end{align*}$

だから，$\set{x\in\R}{f(x)\ge\alpha}\in\mathcal{L}$である．よって，$f$はルベーグ可測関数である．

例２（対数関数）

$I=[0,\infty)$とする．関数$f:I\to\R$を$f(x)=-\log{x}で定めるとき，$f$が$I$上ルベーグ可測関数であることを証明せよ．

任意の$\alpha\in\R$に対して，

$\begin{align*}\set{x\in\R}{f(x)\ge\alpha} &=\set{x\in\R}{-\log{x}\ge\alpha} \\&=\set{x\in\R}{x\le e^{-\alpha}} \\&=(0,e^{-\alpha}]\in\mathcal{L}\end{align*}$

だから，$\set{x\in\R}{f(x)\ge\alpha}\in\mathcal{L}$である．よって，$f$はルベーグ可測関数である．

例３（２次関数）

関数$f:\R\to\R$を

$\begin{align*}f(x)=x^2\end{align*}$

で定めるとき，$f$が$\R$上ルベーグ可測関数であることを証明せよ．

任意に$\alpha\in\R$をとる．

［１］$\alpha\le0$のとき

$\begin{align*}\set{x\in\R}{f(x)\ge\alpha} =\set{x\in\R}{x^2\ge\alpha} =\R\in\mathcal{L}\end{align*}$

である．

［２］$\alpha>0$のとき

$\begin{align*}\set{x\in\R}{f(x)\ge\alpha} &=\set{x\in\R}{x^2\ge\alpha} \\&=\set{x\in\R}{x\le-\sqrt{\alpha},\sqrt{\alpha}\le x} \\&=\bigl(-\infty,-\sqrt{\alpha}\bigr]\cup\bigl[\sqrt{\alpha},\infty\bigr)\end{align*}$

である．一般に可測集合の和集合も可測集合なので$\set{x\in\R}{f(x)\ge\alpha}\in\mathcal{L}$である．

［１］［２］より，$f$はルベーグ可測関数である．

例４（ディリクレ関数）

関数$f:\R\to\R$を

$\begin{align*}f(x)=\begin{cases}1&(x\in\Q)\\0&(x\in\R\setminus\Q)\end{cases}\end{align*}$

で定めるとき，$f$が$\R$上ルベーグ可測関数であることを証明せよ．

この関数$f$をディリクレ関数といい，

$f(4)=f\bra{\frac{1}{2}}=f\bra{\frac{4}{3}}=1$
$f(-\sqrt{2})=f(\pi)=f(\log_{2}{5})=0$

のように，有理数を代入すると１を返し，無理数を代入すると０を返すような関数です．

ディリクレ関数はあまりに不連続なのでリーマン積分不可能ですが，ルベーグ積分は可能な関数の代表例としてよく知られています．

任意に$\alpha\in\R$をとる．

［１］$\alpha\le0$のとき

$\begin{align*}\set{x\in\R}{f(x)\ge\alpha}=\R\in\mathcal{L}\end{align*}$

である．

［２］$0<\alpha\le1$のとき

$\begin{align*}\set{x\in\R}{f(x)\ge\alpha}=\Q\end{align*}$

である．一般に可算集合は可測集合なので$\Q\in\mathcal{L}$だから$\set{x\in\R}{f(x)\ge\alpha}\in\mathcal{L}$である．

［３］$1<\alpha$のとき

$\begin{align*}\set{x\in\R}{f(x)\ge\alpha}=\emptyset\in\mathcal{L}\end{align*}$

である．

［１］〜［３］より，$f$はルベーグ可測関数である．

ルベーグ可測関数であるための必要十分条件

ルベーグ可測関数であるための必要十分条件を２つ紹介します．

必要十分条件１

可測集合$A$と関数$f:A\to\overline{\R}$に対して，次は同値である．

$f$はルベーグ可測関数
任意の$\alpha\in\R$に対して$\set{x\in A}{f(x)>\alpha}\in\mathcal{L}$
任意の$\alpha\in\R$に対して$\set{x\in A}{f(x)\le\alpha}\in\mathcal{L}$
任意の$\alpha\in\R$に対して$\set{x\in A}{f(x)<\alpha}\in\mathcal{L}$

ルベーグ可測関数の定義は集合$\set{x\in A}{f(x)\ge\alpha}$ではなく，

$\set{x\in A}{f(x)>\alpha}$
$\set{x\in A}{f(x)\le\alpha}$
$\set{x\in A}{f(x)<\alpha}$

のどれを用いても全く同じものになるわけですね．

一般に可測集合の補集合は可測集合であり，

$\begin{align*}\set{x\in A}{f(x)\ge\alpha}^c=\set{x\in A}{f(x)<\alpha}\end{align*}$

から$(1)\iff(4)$が成り立つ．同様に$(2)\iff(3)$が成り立つから，あとは$(1)\iff(2)$を示せばよい．

［$(1)\Ra(2)$の証明］任意の$\alpha\in\R$に対して，

$\begin{align*}\set{x\in A}{f(x)>\alpha} =\bigcup_{n=1}^{\infty}\set{x\in A}{f(x)\ge\alpha+\frac{1}{n}}\end{align*}$

である．(1)が成り立つなら

$\begin{align*}\set{x\in A}{f(x)\ge\alpha+\frac{1}{n}}\in\mathcal{L}\quad (n=1,2,\dots)\end{align*}$

であり，ルベーグ可測集合族$\mathcal{L}$は完全加法族だから$\set{x\in A}{f(x)>\alpha}\in\mathcal{L}$である．

［$(2)\Ra(1)$の証明］任意の$\alpha\in\R$に対して，

$\begin{align*}\set{x\in A}{f(x)\ge\alpha} =\bigcap_{n=1}^{\infty}\set{x\in A}{f(x)>\alpha-\frac{1}{n}}\end{align*}$

である．(2)が成り立つなら

$\begin{align*}\set{x\in A}{f(x)>\alpha-\frac{1}{n}}\in\mathcal{L}\quad (n=1,2,\dots)\end{align*}$

であり，一般に可算無限個の可測集合も可測集合だから$\set{x\in A}{f(x)\ge\alpha}\in\mathcal{L}$である．

よって，$f$は$A$上ルベーグ可測関数である．

これらを組み合わせると，次の系が成り立つことも分かりますね．

可測集合$A$と関数$f:A\to\overline{\R}$とに対して，次の集合はいずれも可測集合である．

$\begin{align*}&\set{x\in A}{\alpha<f(x)<\beta},\quad \set{x\in A}{\alpha<f(x)\le\beta}, \\&\set{x\in A}{\alpha\le f(x)<\beta},\quad \set{x\in A}{\alpha\le f(x)\le\beta}\end{align*}$

ただし，$\alpha,\beta\in\R$である．

いずれの集合も可測集合

$\begin{align*}&\set{x\in A}{f(x)>\alpha},\quad \set{x\in A}{f(x)\ge\alpha}, \\&\set{x\in A}{f(x)<\beta},\quad \set{x\in A}{f(x)\le\beta}\end{align*}$

のうちの２つの共通部分で表せる．一般に可測集合の共通部分も可測集合だから，系の４つの集合はいずれも可測集合である．

必要十分条件２

可測集合$A$と関数$f:A\to\overline{\R}$に対して，次は同値である．

$f$はルベーグ可測関数
任意の$r\in\Q$に対して$\set{x\in A}{f(x)\ge r}\in\mathcal{L}$

(1)より(2)の方が弱い条件になっていることに注意しましょう．

すなわち，(2)が成り立てば自動的に無理数$\alpha$に対しても$\set{x\in A}{f(x)\ge\alpha}$が可測集合になるというわけですね．

(1)が成り立てば，任意の$r\in\Q\subset\R$に対して$\set{x\in A}{f(x)\ge r}$は可測集合だから(2)が成り立つ．

一方，(2)が成り立つとし，任意に$\alpha\in\R$をとる．

$\R$における$\Q$の稠密性より$\lim\limits_{n\to\infty}r_n=\alpha$となる単調増加有理数列$\{r_n\}$が存在するから，

$\begin{align*}\set{x\in A}{f(x)\ge\alpha} =\bigcap_{n=1}^{\infty}\set{x\in A}{f(x)\ge r_n}\end{align*}$

が成り立つ．全ての$\set{x\in A}{f(x)\ge r_n}$ ($n=1,2,\dots$)が可測集合であり，一般に可測集合の共通部分も可測集合だから$\set{x\in A}{f(x)\ge\alpha}\in\mathcal{L}$である．

よって，$f$は$A$上ルベーグ可測関数である．