ルベーグ外測度$m^{*}$は直感的には集合の「長さ」を外側から測るものなのでした．
実はルベーグ外測度はルベーグ積分の土台となるルベーグ測度を定義するために必要なもので，ルベーグ外測度$m^{*}$の性質を知っておくことは大切です．
結論から言えば，ルベーグ外測度$m^{*}$は５つの性質［非負値性］［単調性］［平行移動不変性］［劣加法性］［区間の外測度］をもちます．
一方でルベーグ外測度$m^{*}$は「よくない性質」も持ち合わせており，ルベーグ外測度$m^{*}$のままではあまり使い勝手が良くないことも押さえておきたいところです．
この記事では
- ルベーグ外測度の５つの性質
- ルベーグ外測度の不具合とルベーグ測度
- ルベーグ外測度の性質の証明
を順に説明します．
以下ではルベーグ外測度を$m^{*}$で表し，単に「外測度」と呼びます．また，右半開区間$I=[a,b)$の長さ$b-a$を$|I|$と表します．
「ルベーグ積分の基本」の一連の記事
- ルベーグ積分入門
- ルベーグ測度
- ルベーグ可測関数とルベーグ積分
ルベーグ積分の参考文献
以下はルベーグ積分に関するオススメの教科書です．
ルベグ積分入門
ロングセラーの入門書です．専門書ですが，文庫なので安く購入できるのも魅力です．
ルベーグ積分と関数解析
ルベーグ積分から更なるステップに進みたい人向けの教科書です．
ルベーグ外測度の５つの性質
まずはこの記事の本題である外測度の５性質を紹介します．
ルベーグ外測度$m^{*}$は次の５つの性質を満たす．
- ［非負値性］任意の集合$A\subset\R$は$m^{*}(A)\ge0$を満たす．また，$m^{*}(\emptyset)=0$が成り立つ．
- ［平行移動不変性］平行移動で移り合う集合$A, B\subset\R$は$m^{*}(A)=m^{*}(B)$を満たす．
- ［単調性］$A\subset B$を満たす集合$A, B\subset\R$は$m^{*}(A)\le m^{*}(B)$を満たす．
- ［劣加法性］集合$A_1, A_2,\dots\subset\R$は$m^{*}\bra{\bigcup\limits_{n=1}^{\infty}A_n}\le\sum\limits_{n=1}^{\infty}m^{*}(A_n)$を満たす．
- ［区間の外測度］右半開区間$I\subset\R$は$m^{*}(I)=|I|$を満たす．
それぞれ言葉で説明すると，
- 外測度は０以上であり，空集合$\emptyset$の外測度は０
- 平行移動して移り合う２つの集合の外測度は等しい
- 大きい集合の方が外測度も大きい
- 和集合の外測度よりも，それぞれの外測度の和の方が大きいか等しい
- 右半開区間の外測度は$I$の長さに等しい
ということですね．
直感的には外測度が集合の「長さ」を測るものなので，これらの性質が成り立つのはそんなにおかしなことではありませんね．
このうち［非負値性］［区間の外測度］は外測度の定義の記事で証明しました．残りはこの記事の最後に証明します．
ルベーグ外測度の不具合とルベーグ測度
しかし，実は外測度にはあまり嬉しくない性質があります．
ルベーグ外測度の不具合
実は外測度について次の命題が成り立ちます．
（選択公理を仮定すれば）$A\cap B=\emptyset$かつ$m^{*}(A\cup B)\neq m^{*}(A)+m^{*}(B)$を満たす$A,B\subset\R$が存在する．
つまり，２つの集合$A$, $B$に全く被りがなくても
- 和集合$A\cup B$の外測度$m^{*}(A\cup B)$
- 外測度$m^{*}(A)$, $m^{*}(A)$の和$m^{*}(A)+m^{*}(B)$
が等しいとは限らないわけですね．
この性質は「外測度$m^{*}$が長さを測っている」と言うには少々大きい不具合であるように思えます．
そこで，そのような集合が存在しないように$m^{*}$を少し修正することを考えましょう．
いまの命題のような集合$A$, $B$の存在はヴィタリ集合という集合を考えることで証明できます．しかし，ヴィタリ集合はそう簡単な集合ではないので，今は「外測度$m^{*}$には不具合があるらしい」くらいの認識で問題ありません．
ルベーグ測度
上の不具合から
「外測度$m^{*}$の定義域を『良い性質』をもつ集合たちに制限すれば不具合が起きなくなるのではないか？」
と考えてできるものがルベーグ測度と呼ばれるもので，ルベーグ測度はルベーグ積分において本質的に重要な役割を果たします．
ルベーグ測度の定義はのちの記事に譲りますが，結論からルベーグ測度の重要な性質は次の定理です．
$A_1, A_2,\dots$が互いに素（$i\neq j$なら$A_i\cap A_j=\emptyset$）なら
\begin{align*}m\bra{\bigcup\limits_{n=1}^{\infty}A_n}=\sum\limits_{n=1}^{\infty}m(A_n)\end{align*}
が成り立つ．
この性質は測度$m$の完全加法性（や$\sigma$-加法性）などと呼ばれます．
ルベーグ外測度ではさきほどみた不具合があるので，この完全加法性は成り立ちません．
ルベーグ外測度では成り立たないこの性質をもつおかげで，ルベーグ測度$m$は非常に扱いやすいものとなっています．
外測度の性質の証明
それでは上で説明した外測度の性質の証明を与えていきますが，［非負値性］と［区間の外測度］は外測度の定義の記事で証明しました．
よって，あとは［平行移動不変性］と［単調性］と［劣加法性］を示せば良いですね．
平行移動不変性
外測度の平行移動不変性は「平行移動して移り合う集合の外測度は等しい」というものでした．
集合$A, B\subset\R$が平行移動で移り合うとき
\begin{align*}m^{*}(A)=m^{*}(B)\end{align*}
が成り立つ．
集合$X\subset\R$をちょうど$c\in\R$だけ平行移動して得られる集合$\set{x+c\in\R}{x\in X}$を$X+c$と表す．
$A$, $B$が平行移動で移り合うことから，ある$c\in\R$が存在して$A+c=B$が成り立つ．
このとき，$B\subset\bigcup\limits_{n=1}^{\infty}I_n$を満たす右半開区間の列$\{I_n\}$に対して，$A\subset\bigcup\limits_{n=1}^{\infty}(I_n+c)$が成り立つ．
各$n$に対して$|I_n|=|I_n+c|$なので，
\begin{align*}m^{*}(A)=&\inf\set{\dsum_{n=1}^{\infty}|I_n+c|}{\begin{gathered}A\subset\bigcup_{n=1}^{\infty}(I_n+c)\end{gathered}}
\\\le&\inf\set{\dsum_{n=1}^{\infty}|I_n|}{\begin{gathered}B\subset\bigcup_{n=1}^{\infty}I_n\end{gathered}}=m^{*}(B)\end{align*}
が成り立つ．
また，$A=B-c$と考えれば同様に$m^{*}(B)\le m^{*}(A)$が成り立つから，$m^{*}(A)=m^{*}(B)$を得る．
単調性
集合$A, B\subset\R$が$A\subset B$を満たすとき
\begin{align*}m^{*}(A)\le m^{*}(B)\end{align*}
が成り立つ．
$A\subset B$より，右半開区間の列$\{I_n\}$が$B\subset\bigcup\limits_{n=1}^{\infty}I_n$を満たせば$A\subset\bigcup\limits_{n=1}^{\infty}I_n$を満たすので，
\begin{align*}\set{\{I_n\}}{B\subset\bigcup_{n=1}^{\infty}I_n}\subset\set{\{I_n\}}{A\subset\bigcup_{n=1}^{\infty}I_n}\end{align*}
が成り立つ．一般に$X,Y\subset\R$が$X\subset Y$を満たすとき，$\inf{X}\ge\inf{Y}$が成り立つから，外測度$m^{*}$の定義と併せて
\begin{align*}m^{*}(A)=&\inf\set{\dsum_{n=1}^{\infty}|I_n|}{A\subset\bigcup_{n=1}^{\infty}I_n}
\\\le&\inf\set{\dsum_{n=1}^{\infty}|I_n|}{B\subset\bigcup_{n=1}^{\infty}I_n}=m^{*}(B)\end{align*}
が成り立つ．
途中の「一般に$X,Y\subset\R$が$X\subset Y$を満たすとき，$\inf{X}\ge\inf{Y}$が成り立つ」というのは直感的に言えば，「大きい集合の方がより小さい元も属しうるので，大きい集合の方が下限$\inf$が小さくなるか等しい」ということですね．
劣加法性
外測度の劣加法性は「和集合の外測度より，外測度の和の方が大きいか等しい」というものでした．
集合$A_1, A_2,\dots\subset\R$に対して
\begin{align*}m^{*}\bra{\bigcup_{n=1}^{\infty}A_n}\le\sum_{n=1}^{\infty}m^{*}(A_n)\end{align*}
が成り立つ．
有限集合の元の個数のイメージをもてば，この性質は直感的に理解できます．
有限集合$X$の元の個数を$n(X)$で表すことにすると，有限集合$A$, $B$に対して，
\begin{align*}n(A\cup B)=n(A)+n(B)-n(A\cap B)\end{align*}
となりますから，$n(A\cup B)\le n(A)+n(B)$が成り立ちます．
これは$n(A)+n(B)$では$A\cap B$に属する元の個数を$n(A)$, $n(B)$の両方でカウントしますが，和集合$n(A\cup B)$では１回しかカウントしないことが理由ですね．
これと同様に右辺$\sum\limits_{n=1}^{\infty}m^{*}(A_n)$では，$A_i$たちに共通部分があればダブルカウントすることになるため，右辺の方が大きくなりうるわけですね．
一般に$m^{*}\bra{\bigcup\limits_{n=1}^{\infty}A_n}\le\infty$なので，$\sum\limits_{n=1}^{\infty}m^{*}(A_n)=\infty$のときは成り立つ．よって，以下$\sum\limits_{n=1}^{\infty}m^{*}(A_n)<\infty$のときを示す．
任意に$\epsilon>0$をとる．任意の$n$に対して$m^{*}(A_n)<\infty$が成り立つから，外測度$m^{*}(A_n)$の$\inf$の性質より
\begin{align*}m^{*}(A_n)+\frac{\epsilon}{2^n}>\sum_{k=1}^{\infty}|I_n^{(k)}|\quad\dots(*)\end{align*}
なる右半開区間の列$\{I_n^{(k)}\}_k$が存在する．
このとき，$\set{I_n^{(k)}}{n,k=1,2,\dots}$を並べ替えて$\{I_{\ell}\}$と表すと$\bigcup\limits_{n=1}^{\infty}A_n\subset \bigcup\limits_{\ell=1}^{\infty}I_{\ell}$が成り立つから，外測度の定義より
\begin{align*}m^{*}\bra{\bigcup_{n=1}^{\infty}A_n}
\le\sum_{\ell=1}^{\infty}|I_{\ell}|
\le\lim_{L\to\infty}\sum_{\ell=1}^{L}|I_{\ell}|\end{align*}
が成り立つ．
また，任意の$\epsilon>0$, $L\in\N$に対して
\begin{align*}\sum_{\ell=1}^{L}|I_{\ell}|
&\le\sum_{n=1}^{\infty}\sum_{k=1}^{\infty}|I_n^{(k)}|
\\&<\sum_{n=1}^{\infty}\bra{m^{*}(A_n)+\frac{\epsilon}{2^n}}
\\&=\epsilon+\sum_{n=1}^{\infty}m^{*}(A_n)\end{align*}
だから，
\begin{align*}m^{*}\bra{\bigcup_{n=1}^{\infty}A_n}\le\epsilon+\sum_{n=1}^{\infty}m^{*}(A_n)\end{align*}
が成り立つ．$\epsilon$の任意性より$m^{*}\bra{\bigcup\limits_{n=1}^{\infty}A_n}\le\sum\limits_{n=1}^{\infty}m^{*}(A_n)$を得る．
最初に$\sum\limits_{n=1}^{\infty}m^{*}(A_n)=\infty$の場合を除外したのは，$m^{*}(A_n)<\infty$でなければ不等式$(*)$が成り立たないためです．
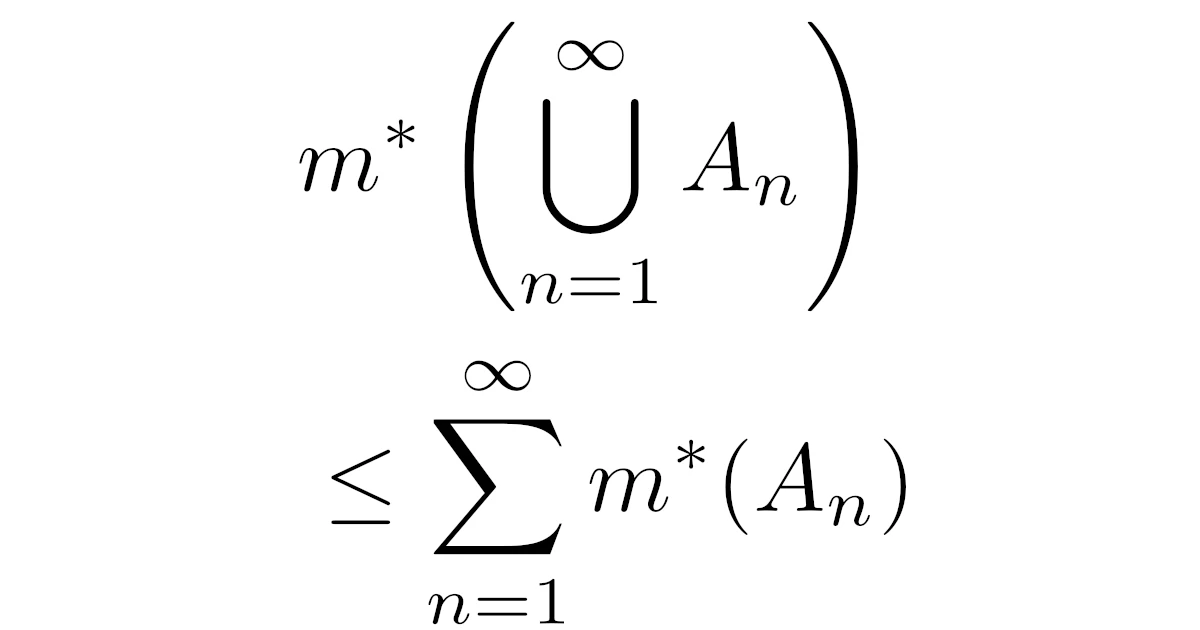
コメント