 位相空間論
位相空間論 連結の定義と具体例|位相空間上の「ひとまとまりな集合」
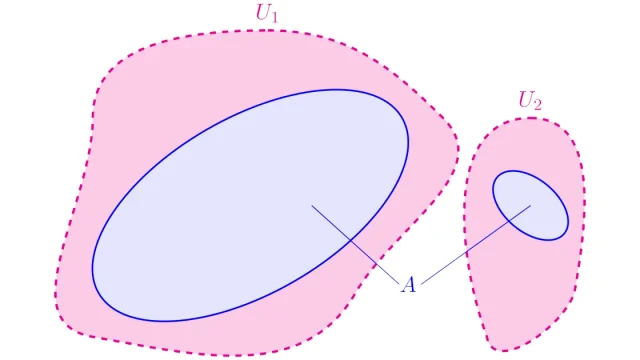
位相空間Xの部分集合Aが「ひとまとまりになっていること」を表す概念として,「連結」と「弧状連結」があります.この記事では「連結」の定義をを丁寧に説明したあと,「弧状連結なら連結」が成り立つことを証明し,「連結な集合の具体例」を紹介しています.
 位相空間論
位相空間論 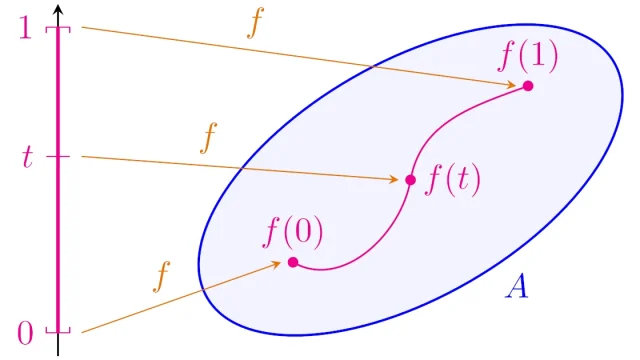 位相空間論
位相空間論 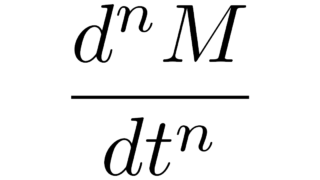 確率論
確率論 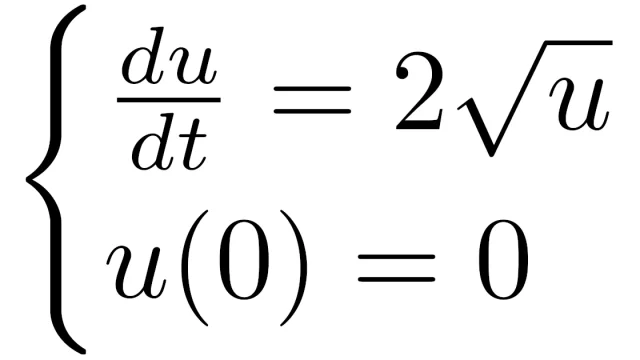 常微分方程式
常微分方程式 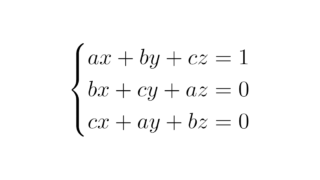 線形代数学
線形代数学 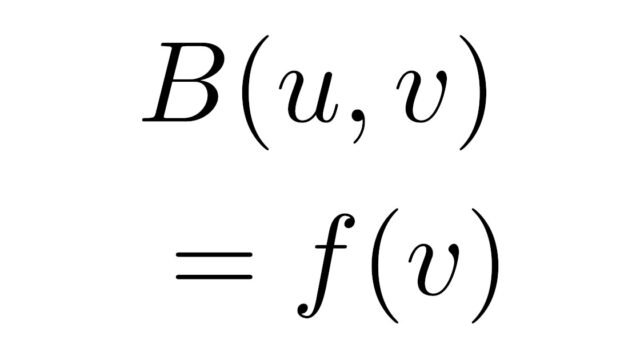 偏微分方程式
偏微分方程式 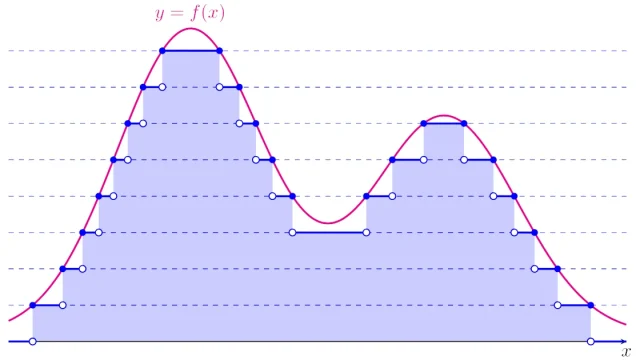 ルベーグ積分の基本
ルベーグ積分の基本 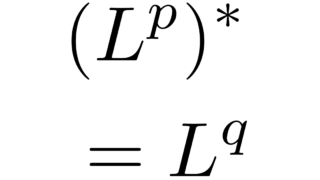 関数空間
関数空間  微分積分学
微分積分学  確率論
確率論