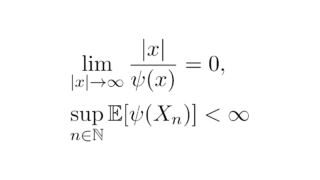 確率論
確率論 確率変数列の一様可積分性の判定|十分条件と必要十分条件
例えば,極限と期待値の順序交換に関する[Vitaliの収束定理]は,一様可積分な確率変数列に対して成り立つ定理である.このように,確率変数列に関する一様可積分性は「良い性質」と言える.この記事では,一様可積分性の十分条件と必要十分条件を説明する.
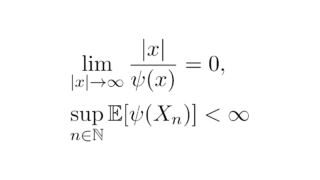 確率論
確率論 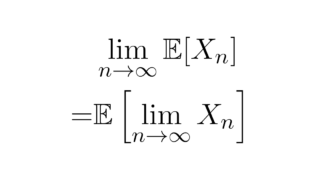 確率論
確率論 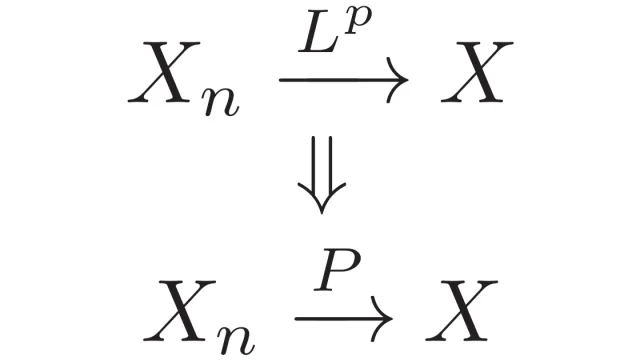 確率論
確率論 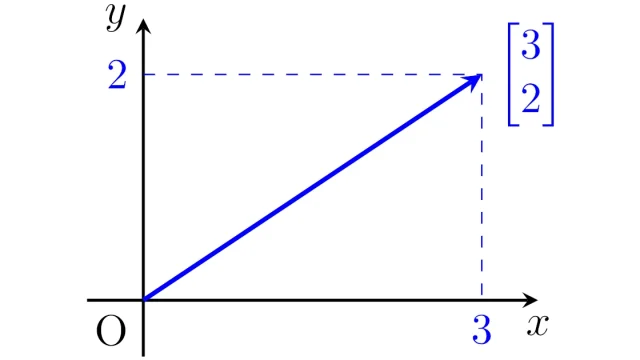 線形代数学の基本
線形代数学の基本 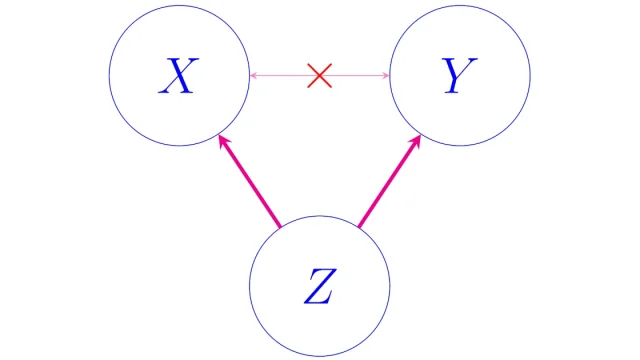 統計学
統計学 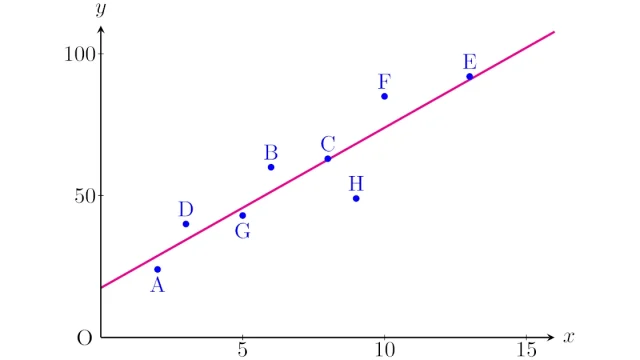 統計学
統計学 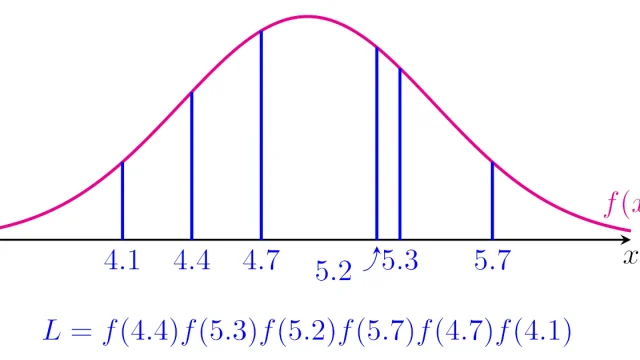 統計学
統計学 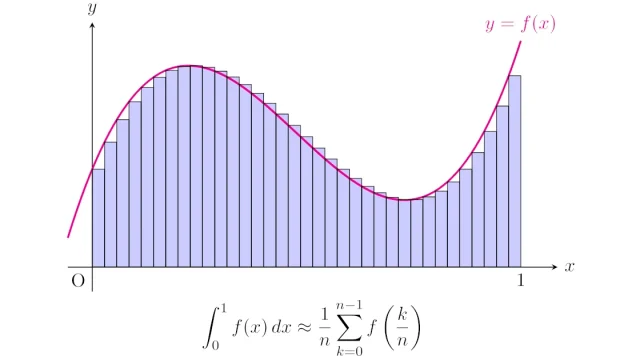 TikZ
TikZ 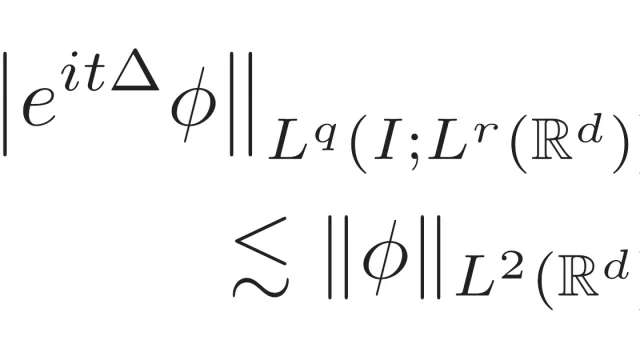 偏微分方程式
偏微分方程式 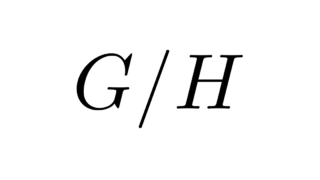 代数学
代数学