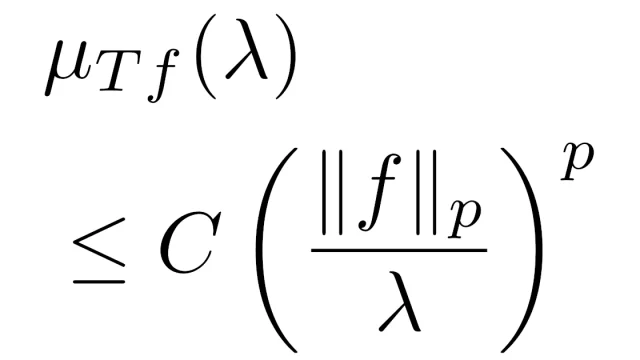 関数解析
関数解析 作用素の弱Lᵖ有界性とマルチンキーヴィッツの実補間定理
マルチンキーヴィッツの実補間定理は,ある不等式を満たす作用素Tが弱L¹有界かつ弱Lᶢ有界(1<g)であるとき,任意のp∈(1,g)に対してTが強Lᵖ有界になるという定理です.この記事では定理の主張と証明をしています.
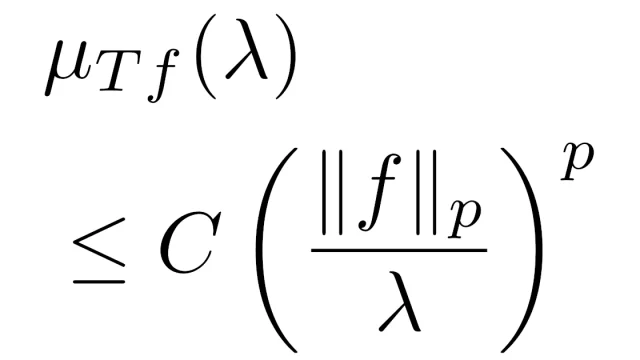 関数解析
関数解析  微分積分学
微分積分学  微分方程式
微分方程式 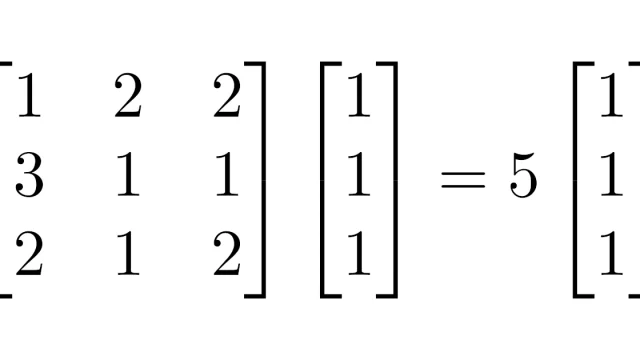 線形代数学
線形代数学 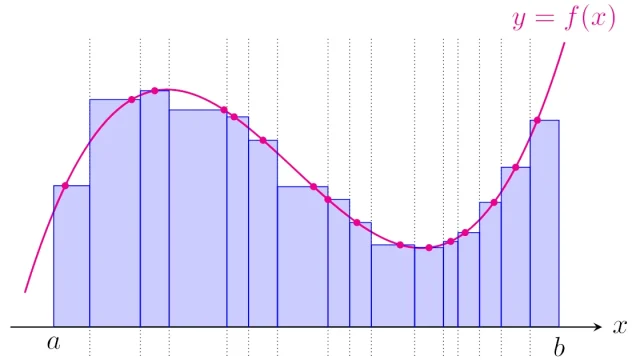 微分積分学
微分積分学  関数解析
関数解析 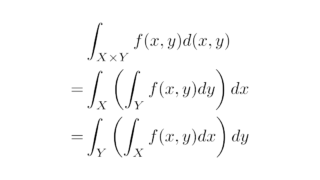 ルベーグ積分
ルベーグ積分 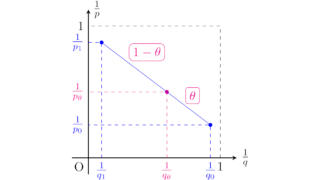 関数解析
関数解析  関数解析
関数解析  大阪市立大学|大学院入試
大阪市立大学|大学院入試