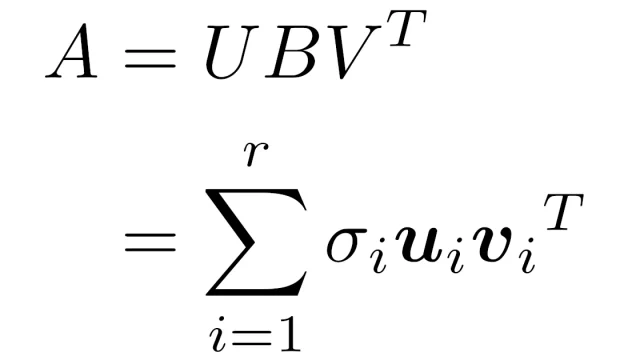 線形代数学
線形代数学 特異値分解(SVD)による低ランク近似|画像圧縮への応用
実対称行列Aに対して直交行列Pをうまくとれば,P⁻¹APを対角行列にすることができます.行列Aが正方行列とは限らない場合にも類似の「特異値分解(SVD)」が成り立ち,特異値分解は画像圧縮やクラスタリングの効率化などに応用されます.
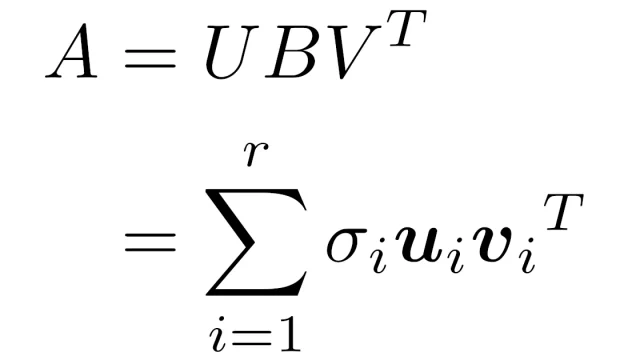 線形代数学
線形代数学 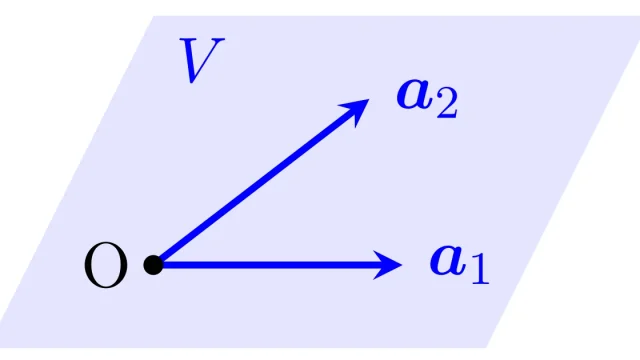 線形空間の基本
線形空間の基本  重要な確率分布
重要な確率分布  確率分布の性質
確率分布の性質  重要な確率分布
重要な確率分布  重要な確率分布
重要な確率分布  重要な確率分布
重要な確率分布  重要な確率分布
重要な確率分布  重要な確率分布
重要な確率分布 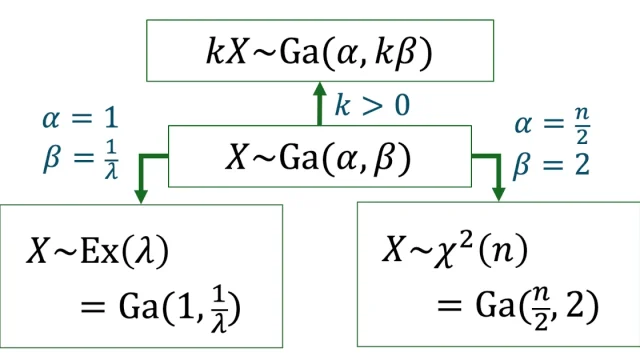 確率分布の性質
確率分布の性質