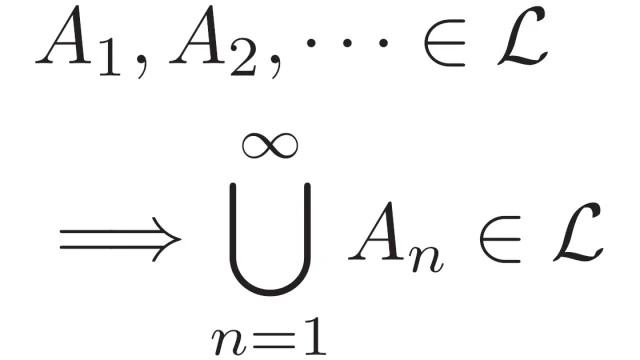 ルベーグ積分の基本
ルベーグ積分の基本 ルベーグ可測集合族は完全加法族|和集合・共通部分の可測性
ルベーグ外測度m*の定義域ルベーグ可測集合全部の族Lに制限してできる写像mをルベーグ測度というのでした.この記事では,Lが完全加法族であることの証明を目標に,基本性質をまとめます.
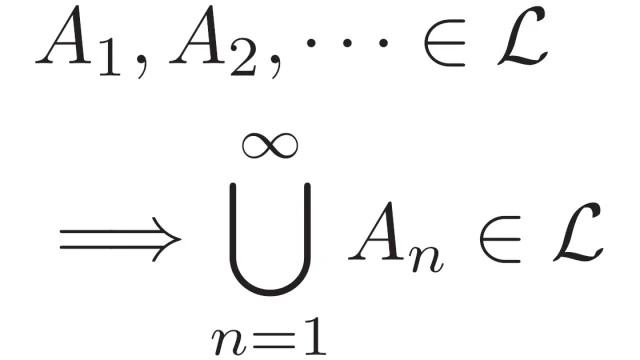 ルベーグ積分の基本
ルベーグ積分の基本 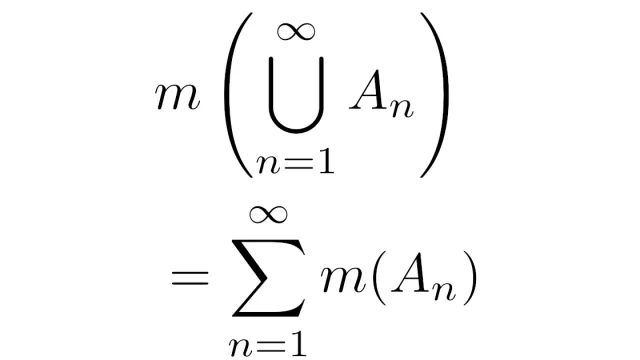 ルベーグ積分の基本
ルベーグ積分の基本 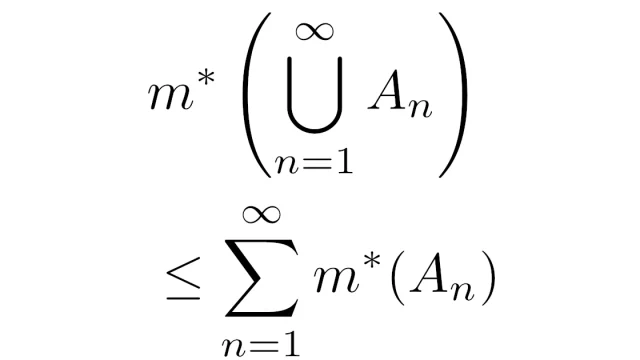 ルベーグ積分の基本
ルベーグ積分の基本  ルベーグ積分の基本
ルベーグ積分の基本  京都大学|大学院入試
京都大学|大学院入試  京都大学|大学院入試
京都大学|大学院入試  微分積分学の基本
微分積分学の基本  微分積分学
微分積分学  微分積分学
微分積分学  集合論
集合論