直観的には,数列$\{a_n\}$を初項から順に足し続けて値$S$に近付くとき,$\{a_n\}$の級数は$S$に収束するといい,$S$を
\begin{align*}\sum\limits_{n=1}^{\infty}a_n\end{align*}
と表します.厳密には
\begin{align*}S_n=a_1+a_2+\dots+a_n\bra{=\sum_{k=1}^{n}a_k}\end{align*}
とおくときの,数列$\{S_n\}$の極限を数列$\{a_n\}$の級数といいます.そのため,級数を考える際には数列の知識をそのまま流用できる部分も多くあります.
また,級数が収束するための必要十分条件であるコーシーの条件と,級数が収束するための十分条件である絶対収束は,級数の収束に関する基本的な条件として知られています.
この記事では
- 級数の直観的な考え方と厳密な定義
- 級数の基本性質
- コーシー条件(級数が収束するための必要十分条件)
- 級数の絶対収束(級数が収束するための十分条件)
を順に解説します.
「微分積分学の基本」の一連の記事
級数の直観的な考え方と厳密な定義
まずは級数の直観的な考え方を説明し,そのあと厳密な定義を説明します.
直観的には初項から順に足した和を級数という
例えば,初項$\frac{1}{2}$,公比$\frac{1}{2}$の等比数列$\{\frac{1}{2^n}\}$を初項から順に無限に足していくことを考えます:
\begin{align*}\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\dots\end{align*}
直観的には,下図のように1×1の正方形を分割してできる長方形の面積の和と捉えることができ,和は1だと思えますね.
つまり,項を足していくとどんどん1に近付いていくということがみてとれます.
この「どんどん近付く」というのはまさに極限の考え方ですから,無限に足していくというのは極限を使って定義すると良さそうです.
級数は初項から第$n$項までの和の極限と定義する
実数列$\{a_n\}$に対して,初項から第$n$項までの和を$S_n$とおく:$S_n=\sum\limits_{k=1}^{n}a_k$.このとき,数列$\{S_n\}$の極限を
\begin{align*}\sum_{k=1}^{\infty}a_k\end{align*}
と表し,実数列$\{a_n\}$の級数(series)という.級数$\sum\limits_{k=1}^{\infty}a_k$に対して,$S_n$のことを(第$n$項までの)部分和(partial sum)をいう.
高校数学では「無限級数」といいますが,大学以降では単に級数と呼ぶのが普通です.
定義から分かるように,$\lim\limits_{n\to\infty}\sum\limits_{k=1}^{n}a_k$のことを$\sum\limits_{k=1}^{\infty}a_k$と表すわけですから,
\begin{align*}\sum_{k=1}^{\infty}a_k=\lim_{n\to\infty}\sum_{k=1}^{n}a_k\end{align*}
ということですね.よって,$\sum\limits_{k=1}^{\infty}$は$\lim\limits_{n\to\infty}\sum\limits_{k=1}^{n}$の略記と捉えることができます.
級数の基本性質
級数も数列の極限ですから,どのようなときに収束・発散するのかを知っておくことは大切です.
収束する級数は定数倍と和をバラバラにできる
級数はあくまで極限ですから,収束する級数は定数倍と和をバラバラにできます.この性質を級数の線形性といいます.
$p,q\in\R$は定数とする.実数列$\{a_n\}$, $\{b_n\}$の級数が収束するなら,実数列$\{pa_n+qb_n\}$の級数も収束して
\begin{align*}\sum_{k=1}^{\infty}(pa_k+qb_k)=p\sum_{k=1}^{\infty}a_k+q\sum_{k=1}^{\infty}b_k\end{align*}
が成り立つ.
第$n$項までの部分和について
\begin{align*}\sum_{k=1}^{n}(p a_k+q b_k)=p\sum_{k=1}^{n}a_k+q\sum_{k=1}^{n}b_k\end{align*}
が成り立つ.実数列$\{a_n\}$, $\{b_n\}$の級数が収束することから,右辺は$n\to\infty$の極限で
\begin{align*}\lim_{n\to\infty}\bra{p\sum_{k=1}^{n}a_k+q\sum_{k=1}^{n}b_k}
=p\sum_{k=1}^{\infty}a_k+q\sum_{k=1}^{\infty}b_k\end{align*}
に収束するから,左辺も$n\to\infty$の極限で収束して
\begin{align*}\sum_{k=1}^{\infty}(pa_k+qb_k)=p\sum_{k=1}^{\infty}a_k+q\sum_{k=1}^{\infty}b_k\end{align*}
が従う.
このように,あくまで級数は部分和の極限であるという意識が大切です.
級数が収束するなら数列は0に収束する
実数列$\{a_n\}$の級数$\sum\limits_{k=1}^{\infty}a_k$が収束するなら$\lim\limits_{n\to\infty}a_n=0$が成り立つ.
$S_n:=a_1+a_2+\dots+a_n$とおき,$S:=\sum\limits_{k=1}^{\infty}a_k$とおく.
$S=\lim\limits_{n\to\infty}S_n=\lim\limits_{n\to\infty}S_{n-1}$だから,
\begin{align*}\lim_{n\to\infty}a_n&=\lim_{n\to\infty}(S_n-S_{n-1})
\\&=\lim_{n\to\infty}S_n-\lim_{n\to\infty}S_{n-1}
\\&=S-S=0\end{align*}
を得る.
この命題の対偶を考えれば,級数の発散条件が得られます.
実数列$\{a_n\}$が0に収束しないなら級数$\sum\limits_{k=1}^{\infty}a_k$は発散する.
ただし,逆は成り立たないことに注意してください.例えば,実数列$\{\frac{1}{n}\}$は0に収束しますが,任意の正の整数$m$に対して
\begin{align*}\sum_{k=1}^{2^m}\frac{1}{k}
&=\frac{1}{1}+\frac{1}{2}+\bra{\frac{1}{3}+\frac{1}{4}}+\bra{\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}}
\\&\quad+\dots+\bra{\frac{1}{2^{m-1}+1}+\dots+\frac{1}{2^m}}
\\&\ge1+\frac{1}{2}+\bra{\frac{1}{4}+\frac{1}{4}}+\bra{\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}}
\\&\quad+\dots+\bra{\frac{1}{2^m}+\dots+\frac{1}{2^m}}
\\&=1+\underbrace{\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\dots+\frac{1}{2}}_{\text{$m$ term}}
\\&=1+\frac{1}{2}m\xrightarrow[]{m\to\infty}\infty\end{align*}
となります.部分和の数列は単調増加であることと併せて,$\sum_{k=1}^{\infty}\frac{1}{k}=\infty$と級数は発散します.
正の整数の逆数和$\sum\limits_{k=1}^{n}\frac{1}{k}$は調和級数(harmonic series)といい,発散する級数として有名です.
等比級数は収束・発散が簡単に判定できる
一般に級数の収束・発散の判定は難しいのですが,等比級数は収束・発散の判定が簡単にできます.この意味で,等比級数は非常に有用です.
等比数列$\{a_n\}$の級数$\sum\limits_{k=1}^{\infty}a_k$を等比級数という.
定数$a,r\in\R$に対して,等比級数$\sum\limits_{k=1}^{\infty}ar^{k-1}$が収束するための必要十分条件は$a=0$または$-1<r<1$が成り立つことである.また,このとき
\begin{align*}\sum\limits_{k=1}^{\infty}ar^{n-1}=\frac{a}{1-r}\end{align*}
が成り立つ. ただし,$a=0$, $r=1$のときは0とみなす.
級数は初項$a$,公比$r$の等比数列の級数である.第$n$項までの部分和を$S_n$とすると,等比数列の和の公式より
\begin{align*}S_n=\frac{a(1-r^n)}{1-r}\end{align*}
である.これが$n\to\infty$の極限で収束するための必要十分条件は,$a=0$または$\lim\limits_{n\to\infty}r^n$が収束すること,すなわち,$a=0$または$-1<r<1$が成り立つことである.
また,$a=0$のときは$0(=\frac{a}{1-r})$に収束し,$a\neq0$のときは$-1<r<1$より$\lim\limits_{n\to\infty}r^n=0$だから$\frac{a}{1-r}$に収束する.
コーシー条件(級数が収束するための必要十分条件)
実数列$\{a_n\}$がコーシー列であることは,実数列$\{a_n\}$が収束するための必要十分条件なのでした.
級数も数列の極限ですから級数にも対応する必要十分条件を考えることができ,この条件をコーシーの条件といいます.
級数が収束することと部分和の数列がコーシー列であることは同値
[コーシーの条件]実数列$\{a_n\}$に対して,次は同値である.
- 級数$\sum\limits_{k=1}^{\infty}a_k$は収束する
- 任意の$\epsilon>0$に対して,ある$N\in\N$が存在して,\begin{align*}m>n>N\Ra|a_{n+1}+a_{n+2}+\dots+a_{m}|<\epsilon\end{align*}が成り立つ.
$S_n=\sum\limits_{k=1}^{n}a_k$とおく.級数の収束の定義から,(1)は実数列$\{S_n\}$が収束することと同値である.
さらに,これは実数列$\{S_n\}$がコーシー列であることと同値である.すなわち,任意の$\epsilon>0$に対して,ある$N\in\N$が存在して
\begin{align*}m>n>N\Ra\abs{S_m-S_n}<\epsilon\end{align*}
が成り立つことと同値である.
\begin{align*}S_m-S_n=a_{n+1}+a_{n+2}+\dots+a_{m}\end{align*}
だから,結局(1)は(2)と同値である.
具体例1(級数$\sum_{k=1}^{\infty}\frac{1}{k^2}$は収束する)
級数$\sum\limits_{k=1}^{\infty}\frac{1}{k^2}$が収束することを示せ.
任意に$\epsilon>0$をとる.$m,n\in\N$を$m>n$とすると
\begin{align*}|a_{n+1}+a_{n+2}+\dots+a_{m}|
=&\frac{1}{(n+1)^2}+\frac{1}{(n+2)^2}+\dots+\frac{1}{m^2}
\\\le&\frac{1}{n(n+1)}+\frac{1}{(n+1)(n+2)}+\dots+\dfrac{1}{(m-1)m}
\\<&\bra{\frac{1}{n}-\frac{1}{n+1}}+\bra{\frac{1}{n+1}-\frac{1}{n+2}}+\dots+\bra{\frac{1}{m-1}-\frac{1}{m}}
\\=&\frac{1}{n}-\frac{1}{m}<\frac{1}{n}\end{align*}
が成り立つ.よって,$N=\lceil{\frac{1}{\epsilon}}\rceil$とおくと,$m>n>N$なら
\begin{align*}|a_m-a_n|<\max\brb{\frac{1}{n},\frac{1}{m}}<\frac{1}{N}<\epsilon\end{align*}
となるから,コーシーの条件より級数$\sum\limits_{k=1}^{\infty}a_k$は収束する.
この解答例を読めば分かるように,コーシーの条件を使えば極限値のアタリがついていなくても収束することが証明できています.これがコーシーの条件(コーシー列)を用いて収束を証明する際のメリットです.
本問の級数$\sum\limits_{k=1}^{\infty}\frac{1}{k^2}$を求める問題はバーゼル問題とよばれており,現在では$\frac{\pi^2}{6}$に収束することが知られています.
級数の絶対収束(級数が収束するための十分条件)
級数の収束は絶対収束と条件収束に分けられます.
絶対収束とは全ての項に絶対値を被せた級数が収束すること
実数列$\{a_n\}$に対して,$\{|a_n|\}$の級数$\sum\limits_{k=1}^{\infty}|a_k|$が収束することを,級数$\sum\limits_{k=1}^{\infty}a_k$は絶対収束(absolute convergence)するという.
絶対収束する級数は,普通の意味でも収束します.
実数列$\{a_n\}$に対して,級数$\sum\limits_{k=1}^{\infty}a_k$が絶対収束すれば収束する.
任意に$\epsilon>0$をとる.級数$\sum\limits_{k=1}^{n}|a_k|$が収束するので,コーシーの条件より,ある$N\in\N$が存在して
\begin{align*}m>n>N\Ra\bigl||a_{m}|+|a_{m-1}|+\dots+|a_n|\bigr|<\epsilon\end{align*}
が成り立つ.よって,$m>n>N$のとき,三角不等式より
\begin{align*}|a_{m}+a_{m-1}+\dots+a_n|\le|a_{m}|+|a_{m-1}|+\dots+|a_n|<\epsilon\end{align*}
となるから,コーシーの条件より級数$\sum\limits_{k=1}^{\infty}a_k$は収束する.
全ての項が非負になることで,級数が扱いやすくなることがよくあります.そのため,収束するかどうかを判定する際には,最初に絶対収束するかどうかを検討するのが基本です.
具体例2(級数$\sum_{k=1}^{\infty}\frac{\sin{k}}{k^2}$は絶対収束する)
級数$\sum\limits_{k=1}^{\infty}\dfrac{\sin{k}}{k^2}$が収束することを示せ.
級数$\sum\limits_{k=1}^{\infty}\abs{\frac{\sin{k}}{k^2}}$の第$n$項までの部分和を$S_n$とおくと,各項が0以上だから実数列$\{S_n\}$は単調増加である.
また,任意の$k\in\N$に対して$|\sin{k}|\le1$だから
\begin{align*}S_n\le\sum_{k=1}^{n}\frac{1}{k^2}\end{align*}
であり,具体例1より右辺は$n\to\infty$の極限で収束するから実数列$\{S_n\}$は上に有界である.
よって,単調有界実数列の収束定理より$\{S_n\}$は収束する.すなわち,級数$\sum\limits_{k=1}^{\infty}\abs{\frac{\sin{k}}{k^2}}$は収束するから,級数$\sum\limits_{k=1}^{\infty}\frac{\sin{k}}{k^2}$は絶対収束する.
したがって,$\sum\limits_{k=1}^{\infty}\frac{\sin{k}}{k^2}$は収束する.
この証明と同じようにすれば,非負実数列$\{a_n\}$, $\{b_n\}$が任意の$n\in\N$に対して$a_n\le b_n$を満たし,級数$\sum_{n=1}^{\infty}b_n$が収束するなら,級数$\sum_{n=1}^{\infty}a_n$が収束することが分かりますね.
具体例3(級数$\sum_{k=1}^{\infty}\frac{(-1)^{k+1}}{k}$は条件収束する)
上の命題で示したように,級数は絶対収束するなら収束しますが,逆は成り立ちません.そこで,この間の収束を条件収束といいます.
実数列$\{a_n\}$の収束する級数$\sum\limits_{k=1}^{\infty}a_k$が絶対収束しないとき,級数$\sum\limits_{k=1}^{\infty}a_k$は条件収束(conditional convergence)するという.
級数$\sum\limits_{k=1}^{\infty}\dfrac{(-1)^{k+1}}{k}$が条件収束することを示せ.
一般に,2つの条件
- $a_1\ge a_2\ge a_3\ge a_4\ge\dots$
- $\lim\limits_{n\to\infty}a_n=0$
を満たす非負実数列$\{a_n\}$に対して,級数$\sum\limits_{n=1}^{\infty}(-1)^{n}a_n$は交項級数であるといい,交項級数は必ず収束する.よって,級数$\sum\limits_{k=1}^{\infty}\dfrac{(-1)^{k+1}}{k}$は収束する.
一方,級数
\begin{align*}\sum_{k=1}^{\infty}\abs{\frac{(-1)^{k+1}}{k}}=\sum_{k=1}^{\infty}\frac{1}{k}\end{align*}
は上の系の直後に示したように正の無限大に発散する.

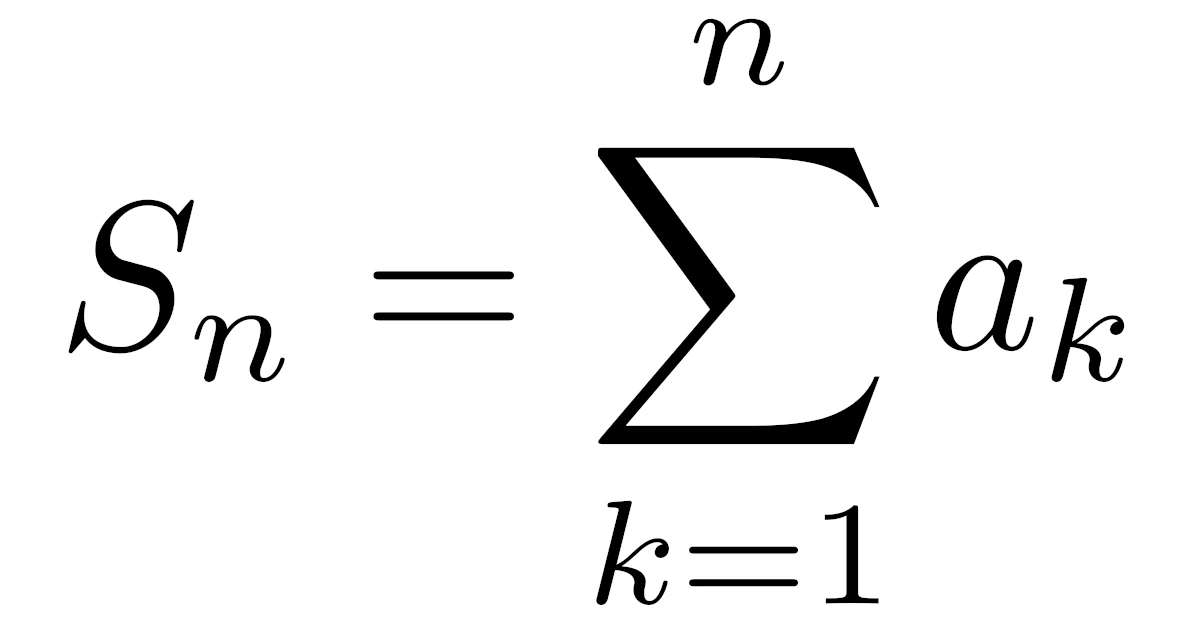

コメント