収束しない実数列｜実数列の３種類の発散と証明の例題

実数列$\{a_n\}$が収束しないとき$\{a_n\}$は発散するといいますが，高校数学でも学ぶように実数列の発散は

正の無限大$\infty$に発散
負の無限大$-\infty$に発散
振動

の３種類に分けられます．

実数列の収束はε-N論法により厳密に定義できたように，実数列の発散もε-N論法と同様の考え方により厳密に定義できます．

この記事では

実数列の３種類の発散の厳密な定義
発散する実数列の具体例

を順に説明します．

「微分積分学の基本」の一連の記事

実数・実数列の性質

微分積分学の参考文献
1. 微分積分学（笠原晧司著）
実数列の３種類の発散の厳密な定義
発散する実数列の具体例

微分積分学の参考文献

以下は微分積分学に関するオススメの教科書です．

微分積分学（笠原晧司著）

数学科など理論系の学生向けの微分積分学の入門書です．基本的な例から発展的な例まで扱われており，バランスの良い教科書です．

実数列の３種類の発散の厳密な定義

まずは３種類の実数列の発散の定義を説明します．

正の無限大$\infty$への発散

具体例から考えてみましょう．

一般項$a_n=n^2$で定まる実数列$\{a_n\}$を考える．

$a_n>1000000$となるには$n$をどんな実数より大きくすればよいか？

この問題は簡単ですね．

$a_n=n^2$, $n>0$だから，

$\begin{align*}a_n>1000000\iff n>1000\end{align*}$

なので，例えば$n$を1000より大きくすればよい．

いまの問題は$a_n>1000000$でしたが，「$a_n>10^{100}$となるには$n$をどんな実数より大きくすればよいか？」という問題に変わっても，同じように解けますね．

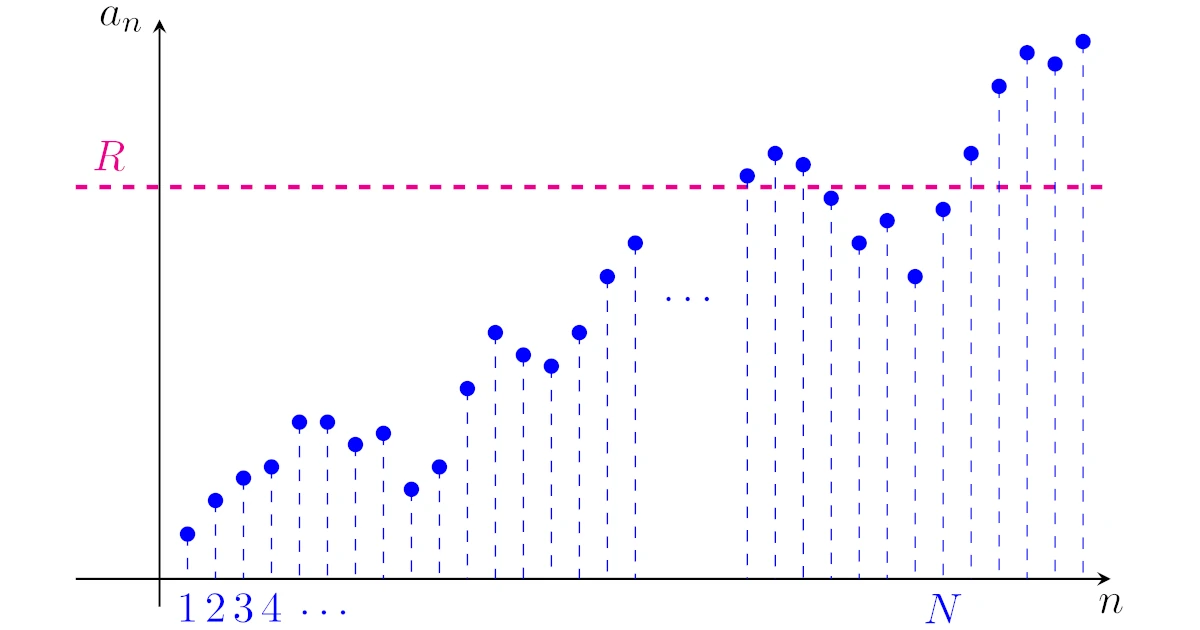
つまり，どんな$R>0$に対しても，$n$が十分大きいところで常に$a_n>R$となるようにできますね．

この性質をもつ数列は正の無限大$\infty$に発散すると言います．

実数列$\{a_n\}$が（正の）無限大$\infty$に発散するとは，任意の$R>0$に対して，ある$N\in\N$が存在して，

$\begin{align*}n>N\Ra a_n>R\end{align*}$

が成り立つことをいう．また，このとき$\lim\limits_{n\to\infty}a_n=\infty$や$a_n\to\infty$ ($n\to\infty$)などと表す．

全称記号$\forall$と存在記号$\exists$を用いれば，上の定義は

$\begin{align*}\forall R>0\quad\exists N\in\N\quad\text{s.t.}\quad[n>N\Ra a_n>R]\end{align*}$

とも表せますね．

少し砕けた言い方をすれば，実数列$\{a_n\}$が正の無限大$\infty$に発散するとは「どんなに大きな正の数$R$に対しても，十分大きな正の整数$N$をうまくとって，$n>N\Ra a_n>R$が成り立つようにできる」ということになります．

また，上の具体例からも分かるように，$N$は$R$に応じて決めてよいという点は大切です．

ε-N論法による実数列の収束の定義と考え方は似ていますね．

負の無限大$-\infty$への発散

正の無限大$\infty$への発散と同様ですが，ここでも具体例から考えてみましょう．

一般項$a_n=-\dfrac{1}{2}n$で定まる実数列$\{a_n\}$を考える．

$a_n<-10000$となるには$n$をどんな実数より大きくすればよいか？

この問題も簡単ですね．

$a_n=-\dfrac{1}{2}n$だから，

$\begin{align*}a_n<-10000\iff n>20000\end{align*}$

なので，例えば$n$を20000より大きくすればよい．

先ほどと同じように，どんな$S<0$に対しても，$n$が十分大きいところで常に$a_n<S$となるようにできますね．

この性質をもつ数列は負の無限大$-\infty$に発散すると言います．

実数列$\{a_n\}$が負の無限大$-\infty$に発散するとは，任意の$S<0$に対して，ある$N\in\N$が存在して，

$\begin{align*}n>N\Ra a_n<S\end{align*}$

が成り立つことをいう．また，このとき$\lim\limits_{n\to\infty}a_n=-\infty$や$a_n\to-\infty$ ($n\to\infty$)などと表す．

こちらも実数列$\{a_n\}$が負の無限大$-\infty$に発散するとは「どんなに小さな負の数$S$に対しても，十分大きな正の整数$N$をうまくとって，$n>N\Ra a_n<S$が成り立つようにできる」といえますね．

また，上の具体例からも分かるように，$N$は$S$に応じて決めてよいという点は大切です．

振動

振動は次で定義されます．

実数列$\{a_n\}$が振動するとは，$\{a_n\}$は発散する（収束しない）が，正の無限大$\infty$にも負の無限大$-\infty$にも発散しないことをいう．

「発散」という言葉からは「どこかに飛んでいく」ようなイメージを持ちそうですが，収束しない数列は全て発散するということに注意してください．

発散の中でも

項がどこまでも大きくなっていく正の無限大$\infty$への発散
項がどこまでも小さくなっていく負の無限大$-\infty$への発散

が定義されるわけですが，そのどちらでもない発散もあり得ます．そのような「残りモノ」の発散を振動というわけですね．

発散する実数列の具体例

具体的に３種類の発散を定義に従ってきちんと示しましょう．

例１（無限大$\infty$に発散）

一般項$a_n=n^2$で定まる実数列$\{a_n\}$が$\lim\limits_{n\to\infty}a_n=\infty$となることを示せ．

任意に$R>0$をとる．$N$を$\sqrt{R}$以上の最小の整数とすると，$n>N$なら

$\begin{align*}a_n=n^2>N^2\ge R\end{align*}$

となるので，実数列$\{a_n\}$は無限大$\infty$に発散する．

一般に$x\in\R$以上の最小の整数は$\lceil x\rceil$と表し，この関数$\lceil\cdot\rceil$を天井関数といいます．よって，いまの解答の$N$は$N=\left\lceil\sqrt{R}\right\rceil$と表せます．

初手として，任意の$R>0$をとるのは鉄板です．

この$R$に対して，どれくらい大きな$N\in\N$をとれば良いのかが問題となるわけですが，$N^2\ge R$を解くと$N\ge\sqrt{R}$となります．

よって，$N\ge\sqrt{R}$となる正の整数$N$を取ればよいので，$N$を$\sqrt{R}$以上の最小の整数$\left\lceil\sqrt{R}\right\rceil$としたわけですね．

例２（負の無限大$-\infty$に発散）

一般項$a_n=-n^2-n$で定まる実数列$\{a_n\}$が$\lim\limits_{n\to\infty}a_n=-\infty$となることを示せ．

任意に$S<0$をとる．$N$を$\sqrt{-S}$以上の最小の整数とすると，$n>N$なら

$\begin{align*}a_n=-n^2-n<-n^2<-N^2\le S\end{align*}$

となるので，実数列$\{a_n\}$は負の無限大$-\infty$に発散する．

やはり負の無限大$-\infty$への発散を示す際も，任意の$S<0$を初手にとるのは鉄板です．

今回は$n>N\Ra-n^2-n<S$となる$N\in\N$を考えればいいわけですが，$-N^2-N<S$を解くのは少し面倒です（解いても構いません）．

そこで，$a_n<-n^2$と少し緩めて解きやすい$-N^2\ge S$に持ち込み，この解$N\ge\sqrt{-S}$から$N=\left\lceil\sqrt{-S}\right\rceil$とおいたわけですね．

例３（振動）

一般項$a_n=(-1)^{n}n$で定まる実数列$\{a_n\}$が振動することを示せ．

どんどん振り幅が大きくなっていくので振動しそうですね．振動は「残りモノ」の発散なので，

収束しない
正の無限大$\infty$に発散する
負の無限大$-\infty$に発散する

の３つを示せばいいですね．

実数列$\{a_n\}$が収束せず，正の無限大$\infty$にも負の無限大$-\infty$にも発散しないことを示せばよい．

収束しないことの証明

背理法により示す．実数列$\{a_n\}$が$\alpha$に収束すると仮定すると，任意の$\epsilon>0$に対して，ある$N\in\N$が存在して，

$\begin{align*}n>N\Ra|a_n-\alpha|<\epsilon\end{align*}$

が成り立つ．$\epsilon$は任意なので，$\epsilon=1$として$n=N+1,N+2$の場合を考えると

$\begin{align*}|a_{N+1}-\alpha|<1,\quad |a_{N+2}-\alpha|<1\end{align*}$

が成り立つので，

$\begin{align*}|a_{N+1}-a_{N+2}|=&|(a_{N+1}-\epsilon)-(a_{N+2}-\epsilon)| \\\le&|a_{N+1}-\epsilon|+|a_{N+2}-\epsilon|<2\end{align*}$

となる．ただし，$x,y\in\R$に対して，三角不等式$|x+y|\le|x|+|y|$が成り立つことを用いた．一方，

$\begin{align*}|a_{N+1}-a_{N+2}|=|(-1)^{N+1}(N+1)-(-1)^{N+2}(N+2)|=2N+3\end{align*}$

であるが，$2N+3<1$は成り立たないから矛盾である．よって，実数列$\{a_n\}$は収束しない．

正の無限大$\infty$には発散しないことの証明

背理法により示す．$\lim\limits_{n\to\infty}a_n=\infty$と仮定すると，任意の$R>0$に対して，ある$N\in\N$が存在して，

$\begin{align*}n>N\Ra a_n>R\end{align*}$

が成り立つ．しかし，$a_{N+1}$と$a_{N+2}$のいずれか一方は負だから矛盾である．

よって，実数列$\{a_n\}$は無限大$\infty$には発散しない．

負の無限大$-\infty$に発散しないことの証明

背理法により示す．$\lim\limits_{n\to\infty}a_n=-\infty$と仮定すると，任意の$S<0$に対して，ある$N\in\N$が存在して，